［奇偶関数／対数の指数］積分道場#68、#83を解いてみよう

今回もやってきました、積分道場のお時間です。
今回は 第68問 と 第83問 とを一気にやってみます。

ほっほぉ～、$(-1,\;1)$での定積分ですか。
任意の奇関数$I$とまたもや任意の偶関数$O$に対して
$\displaystyle\qquad {}^\exists a\in\mathbb{R};\;\int_{-a}^aI(x)\,{\rm d}x=0,\quad\int_{-a}^{a}O(x)\,{\rm d}x=2\int_0^aO(x)\,{\rm d}x$
になる性質を使っていこうと思います。
奇関数は$I(-x)=-I(x)$、偶関数は$O(-x)=O(x)$となるような関数ですね。
$(-a,\;a)$とかじゃなくても、$(-4,\;7)$のように正と負をまたぐ範囲での定積分でも使えると思います。

$\displaystyle\qquad a,\;b>0,\;a< b;\quad\int_{-a}^bI(x)\,{\rm d}x=\cancel{\int_{-a}^aI(x)\,{\rm d}x}+\int_a^bI(x)\,{\rm d}x=\int_a^bI(x)\,{\rm d}x$
になるので、マイナスを入れなくても済む。

さて、話がそれてしまいました。やっていきましょう。
まぁこれは展開したほうがはやいかな～。

$$\begin{aligned} \int_{-1}^1 (1+x+x^2)^2\,{\rm d}x&=\int_{-1}^1(1+x^2+x^4+2x^2+2x^3+2x)\,{\rm d}x \\ &=2\int_0^1(1+3x^2+x^4)\,{\rm d}x \\ &=2\left[x+x^3+\frac15x^5\right]^1_0 \\ &=2\left(1+1+\frac15\right)=\frac{22}5\quad\blacksquare \end{aligned}$$

指数に$\ln$があるとそれを引き下げたくなりますよね。
底変換を使って$x$を引きずりだしてやります。
$\displaystyle \ln x=\frac{\log_5 x}{\log_5 e}=\ln5\log_5x$から$5^{\ln x}=5^{\ln 5\log_5 x}=x^{\ln 5}$なので

$$\begin{aligned} \int_1^e5^{\ln x}\,{\rm d}x&=\int_1^ex^{\ln 5}\,{\rm d}x \\ &=\left[\frac1{\ln 5+1}x^{1+\ln 5}\right]^e_1 \\ &=\frac1{\ln 5+1}(e^{1+\ln 5}-1^{1+\ln 5}) \\ &=\frac1{\ln 5+1}(e\cdot e^{\ln 5}-1) \\ &=\frac{5e-1}{\ln 5+1}\quad\blacksquare \end{aligned}$$

はい、なんかちょっと汚い形になりましたが一応問題ないと思います。
検証た～いむ。Geogebraくんよろしくです

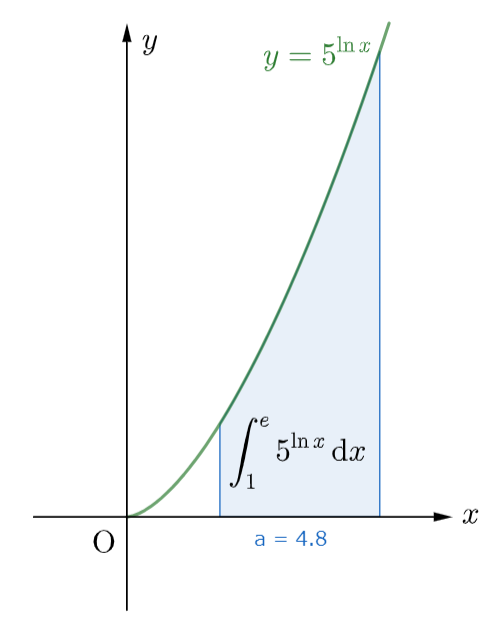
おっ、やったね。$\displaystyle\frac{5e-1}{\ln5+1}$も$\approx4.8$なので大丈夫そうです。

以上！　次の記事でお会いしましょ～。