TREE数、tree数、 SCG数、SSCG数の近似値

いろいろネットを漁ったことによっていくつかの近似値を得ることに成功した。
fを急増化関数、φは多変数ヴェブレン関数、θは1変数関数ならヴァイアーマンのθ関数、2変数関数ならフェファーマンのθ関数、Ψを拡張ブーフホルツのΨ関数とする。任意の関数F(n)について、
F_1(n)=F(n),F_α+1(n)=(F_α)^n(n),
F_α(n)=F_α n (αは極限順序数)
とする。ただし^nは関数の合成回数を表す。
また、SVO=θ(Ω^ω) LVO=θ(Ω^Ω) BHO=Ψ(Ω_2) BO=Ψ(Ω_ω)　TFB=Ψ(ε_((Ω_ω)+1))とする。

①tree数

https://recursion-theory.blogspot.com/2020/05/lower-bounds-for-tree4-and-tree5.html
tree(1)=2
tree(2)=5
tree(3)≧2^18-4
tree(4)>f_ε_(ω^2)(グラハム数)
tree(5)>f_φ(1,0,0,0)(グラハム数)
tree(n+2)>f_θ(Ω^n)(グラハム数) (n>3)
tree(n+2)>f_SVO(n) (3<n≦グラハム数)
tree(1.00001n+2)>f_SVO(n)
tree(n+2)≒f_SVO(n)

これらの結果が分かっている。tree数はSVOレベルよりはるかに強い可能性は低いと思われる。

②TREE数

TREE(1)=1
TREE(2)=3
TREE(3)>tree_3(tree_2(tree(8)))
≒f_SVO+2(f_SVO+1(f_SVO(6)))
>f_SVO+3(2)
TREE(3)>{3,{3,{3,8[1[1-1,2]2]2},2[1[1-1,2]2]2},3[1[1-1,2]2]2}
≒{3,3,4[1[1-1,2]2]2}>{3,6,3[1[1-1,2]2]2}
最後の式はバードによるものだ。
https://www.youtube.com/watch?v=j98suMfW1tc
TREE(3)≒{100,100[1[2/1,2-2]2]2}
と紹介されているが、弱い評価であることは間違いない。
TREE(4)以降の近似値はよく分かっていない。
巨大数を扱う動画ではTREE(4)をあらゆるバード配列より大きいと表現されることもあるが、ありえない。

TREE関数はtreeよりはるかに強いことが分かっていて、SSCGより弱いと信じられている。
よってSVOより強くBOより弱い。
そのためθ((Ω^ω)×ω)レベルだと推測されている。
よってある程度大きなnについて、
TREE(n)≒f_θ((Ω^ω)×ω)(n)　である。
TREEはLVOレベルだと主張する声もある。

③SSCG数

https://googology.fandom.com/wiki/Talk:Subcubic_graph_number#growth_rate_of_SCG.28k.29_upper-bounded_by_TFB_ordinal.3F

SSCG(0)=2
SSCG(1)=5
SSCG(2)≧3×2^(3×2^95)-8≒10^(3.5775×10^28)
SSCG(3)についてはHyp cosによって以下の近似値が分かっている。
https://googology.fandom.com/wiki/User_blog:Hyp_cos/SCG(n)_and_some_related
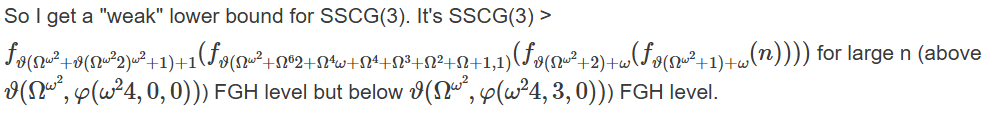SSCG(3の近似値)
私はヴァイアーマンのθ関数の意味がよく分かっていないため、バードでどのように近似できるかは分からない。
https://www.youtube.com/watch?v=j98suMfW1tc
SSCG(3)≒{100,100[1[1/1,1,2-2]1[1[3/2-2]1[3/2-2]1[3/2-2]1[3/2-2]2]2]2}
と紹介されているが、弱い評価であることは間違いない。

少なくとも
SSCG(3)>TREE_4(3)　は成立するのは既に分かっている。

PSSCG(n)は、元のSSCGのルールと異なり、平面グラフのみに限定したものだ。PSCGについても同様である。
PSSCG(n)≧SSCG(n)は任意の自然数nで成立し、
SCG(n)≧PSCG(n)>f_Ψ(Ω_ω)(n)が成立するのはとっくに分かっているため、SSCG(n)≧PSSCG(n)>f_Ψ(Ω_ω)(n)も十分大きなnで成立するとかんがえられてる。これは間違いないと私は考えている。
CLG理論
これはPSCG及びPSSCGがBOレベルであることを示す根拠だ。
グラフの双対を捉えるCLG変換を繰り返して空グラフになるまでの回数をnとして、そのグラフをlevelnとする。
level1の構造である木(Forests)がε0レベル、つまりψ(Ω)レベルであり、level2の構造は、多角形同士の共有辺が常に長さ1であるような、単純なものに限定するとψ(Ω_2)レベルであり、複雑なものを含めてもψ(Ω_3)は超えないことが分かっている。一般にlevelnのグラフはψ(Ω_n)に対応すると考えられている。

ここで重要な事実は、CLG変換後は常に単純グラフということだ。
これはSCGが常に1つ上のlevelにあることを意味するため、後述するSSCGとSCGが線形レベルで同じであることを強く示唆している。

もちろん、SSCGより、PSSCGの方が弱く、BOの近似度が高いだろう。ワグナーの定理より、PSCGに含まれず、SCGに含まれる図形はK3,3であることに留意して、
SSCG(4)=PSSCG(4)
SSCG(5)=PSSCG(6)+1
SSCG(6)≧PSSCG(12)+6
SSCG(7)>PSSCG_PSSCG(7)(7)
が分かっている。
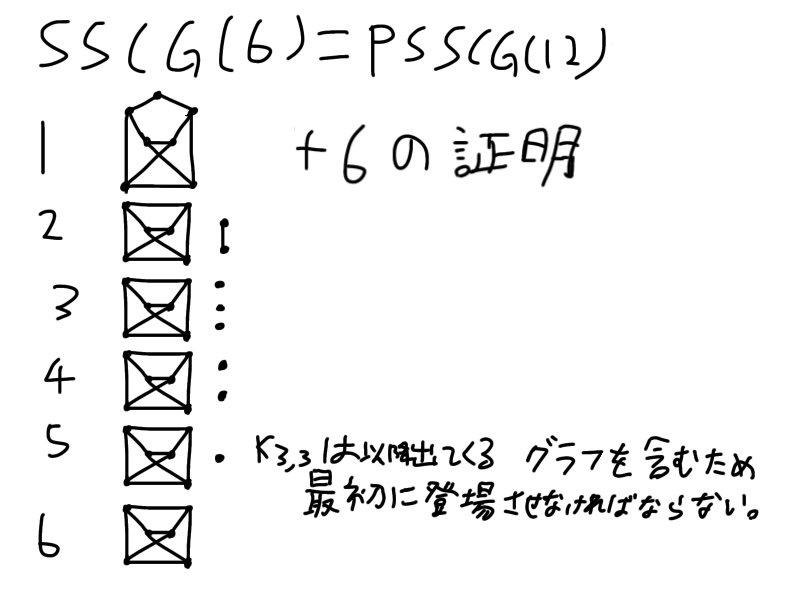SSCG(6)の公式の証明
これらを活用し、
SSCG(4)≒f_Ψ(Ω_ω)(4)≒{3,3[1[1[1[2(/_4)2]2]2]2]2}
SSCG(5)≒f_Ψ(Ω_ω)(6)≒{3,3[1[1[1[1[1[2(/_6)2]2]2]2]2]2]2}
SSCG(6)≒f_Ψ(Ω_ω)(12)≒{3,12[1[2(/_1,2)2]2]2}
SSCG(7)>PSSCG_(f_Ψ(Ω_ω)(7)+1)(7)>f_Ψ(Ω_ω)+ω(f_Ψ(Ω_ω)(7))≒{3,{3,7[1[2(/_1,2)2]2]2},1,2[1[2(/_1,2)2]2]2}

{3,3,2,2,[1[2(/_1,2)2]2]2}
SSCG(4)~SSCG(6)は信憑性が低いが、SSCG(7)は、PSSCG(n)のnが十分大きくなることで評価の信頼度が上がると考えらえる。
じゃあSSCG(8)はどうだろうか。
SSCG(n)≧CSSCG(n)を利用して、
CSSCG(8)の評価
このことから
CSSCG(8)>PCSSCG_ω+2(PCSSCG_ω+2(4))が分かる。
PCSSCGがBOレベルだと仮定すると、
SSCG(8)>CSSCG(8)>(f_Ψ(Ω_ω)+ω+2)^2(4)≒{3,{3,4,3,2[1[2(/_1,2)2]2]2},3,2,[1[2(/_1,2)2]2]2}>{3,3,4,2,[1[2(/_1,2)2]2]2}
が得られる。ここで疑問点は、本当にPCSSCGがBOレベルなのか、ということだ。CLG理論に基づくならば、その答えは間違いなくyesなのだが。

★SSCG(3),SSCG(4),SSCG(5)のさらに強い評価を得るには

https://googology.fandom.com/wiki/Talk:Subcubic_graph_number#growth_rate_of_SCG.28k.29_upper-bounded_by_TFB_ordinal.3F
ここにヒントが載っている。CLG理論に基づくと、SSCG(4)はΨ(Ω_2)より強くΨ(Ω_3)より弱く、SSCG(5)はΨ(Ω_3)より強くΨ(Ω_4)より弱い。そのため載せた近似はあまりにも精度が低い。
実はSSCG(3)は従来の近似よりも少し強いことが分かってきた。
https://googology.fandom.com/wiki/Talk:Subcubic_graph_number#Actual_strength_of_SCG_function
によると、Hyp cosのSSCG(3)の配列候補は正確ではなく、よりよいものがあると紹介している。
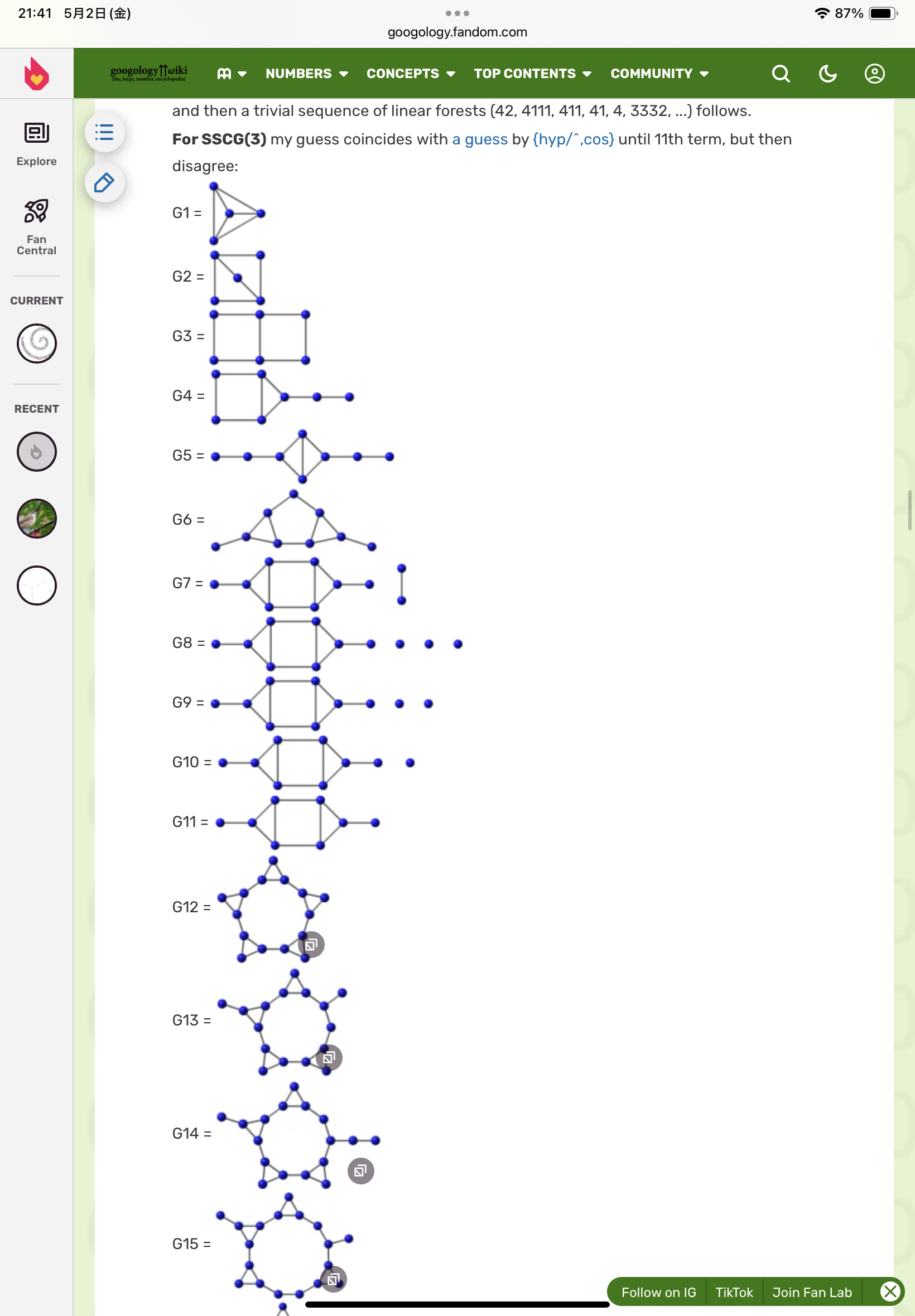変形のようす1
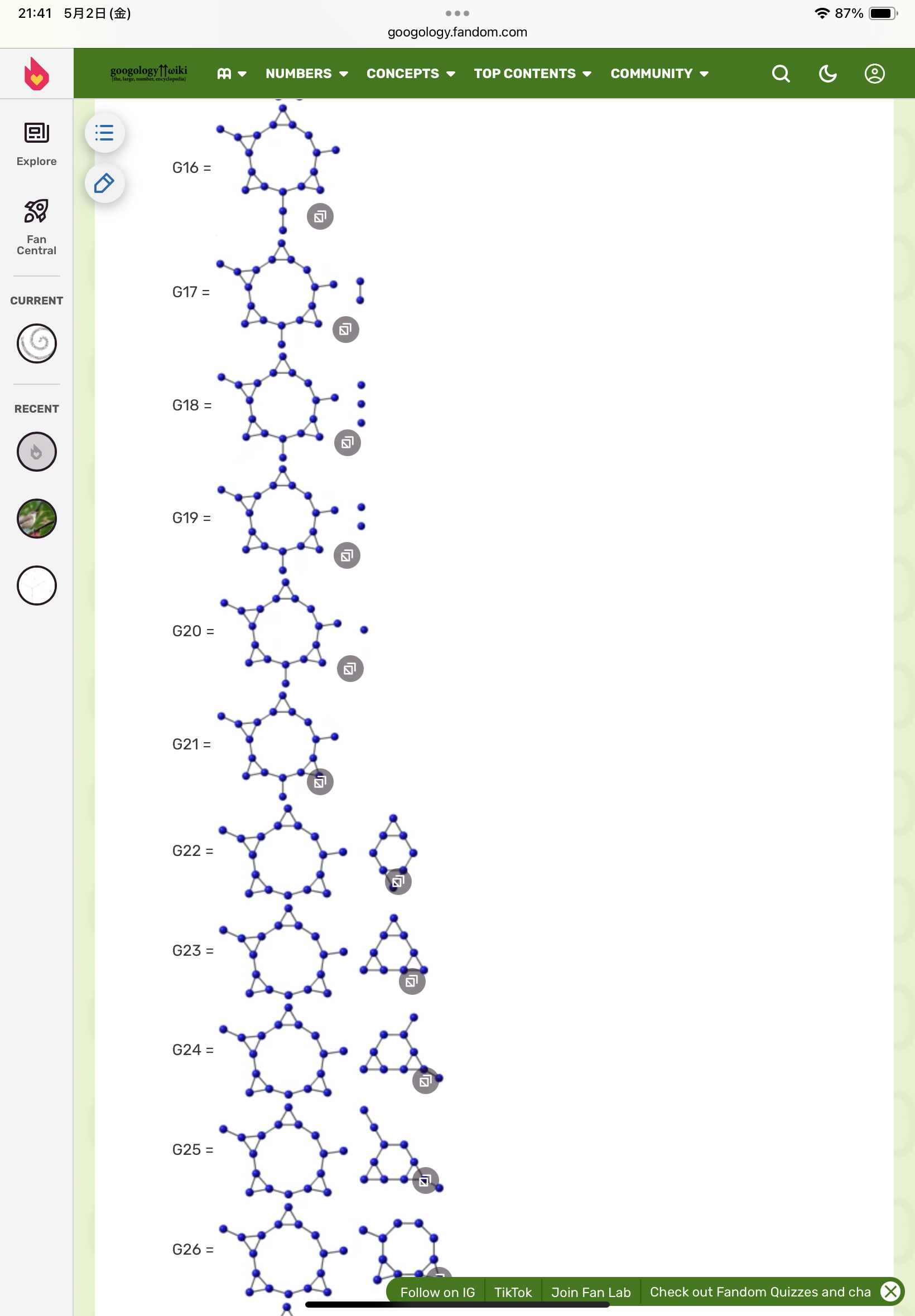変形のようす2
変形のようす3
この後の変形は自分で用意した
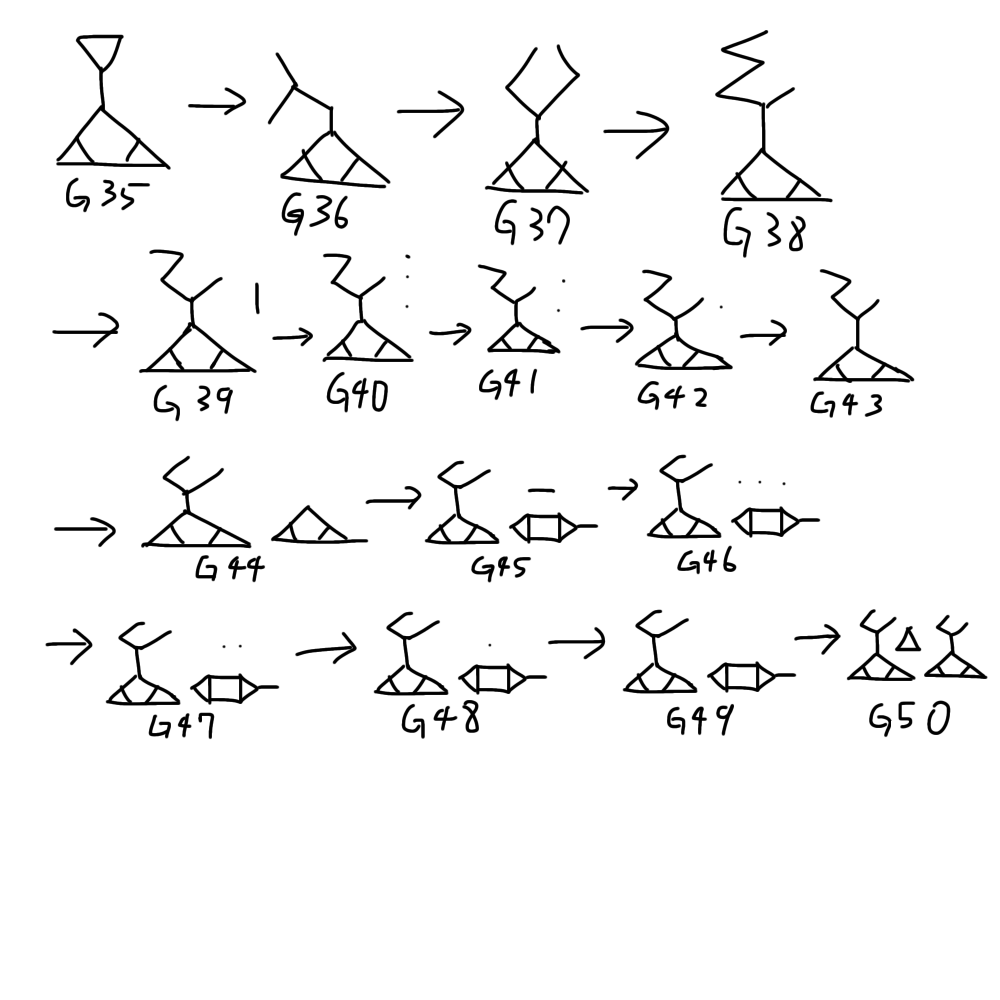変形のようす4
三角形を獲得するまで変形した。
ここで各順序数の対応する図形を参照して
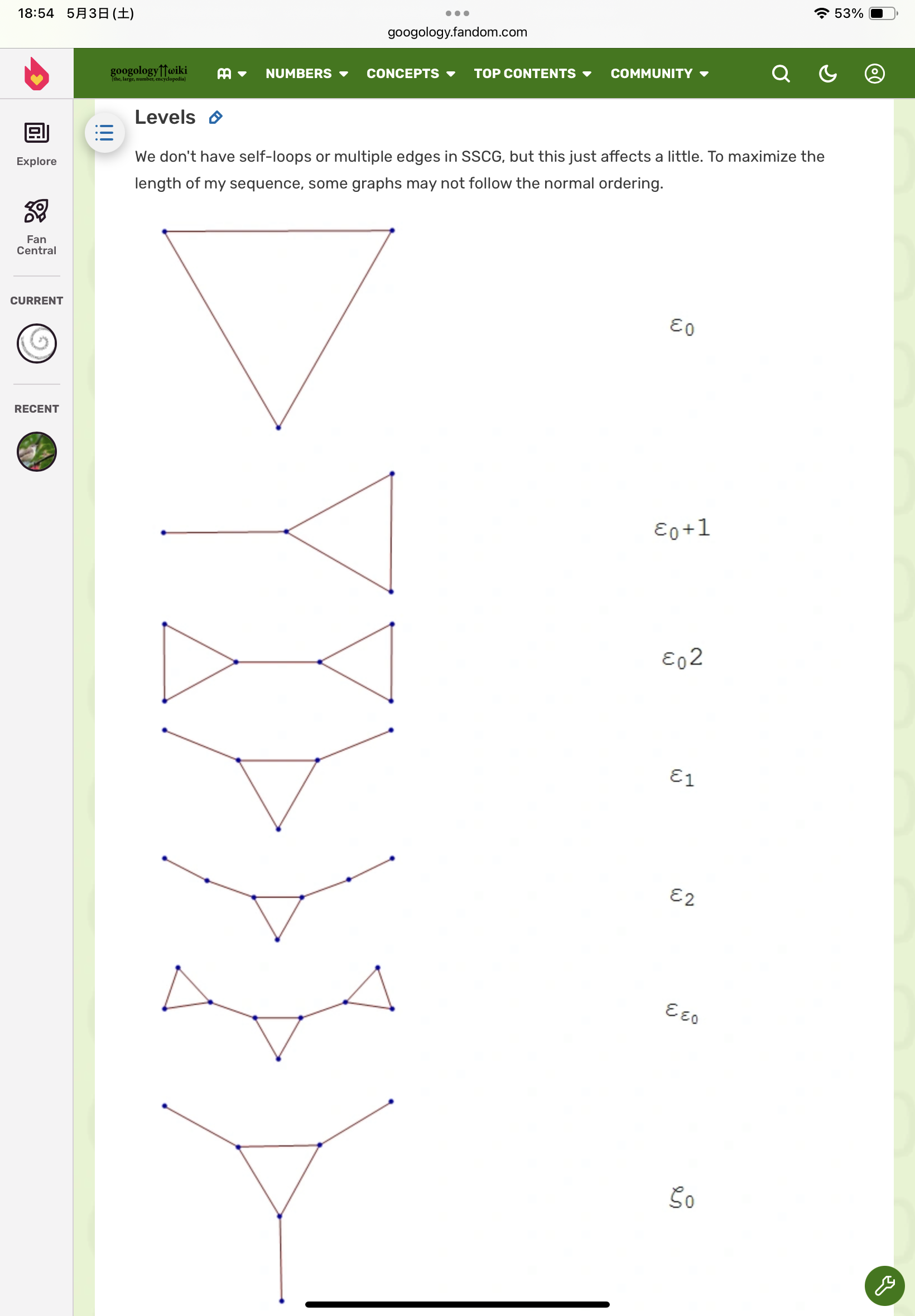順序数1
順序数2
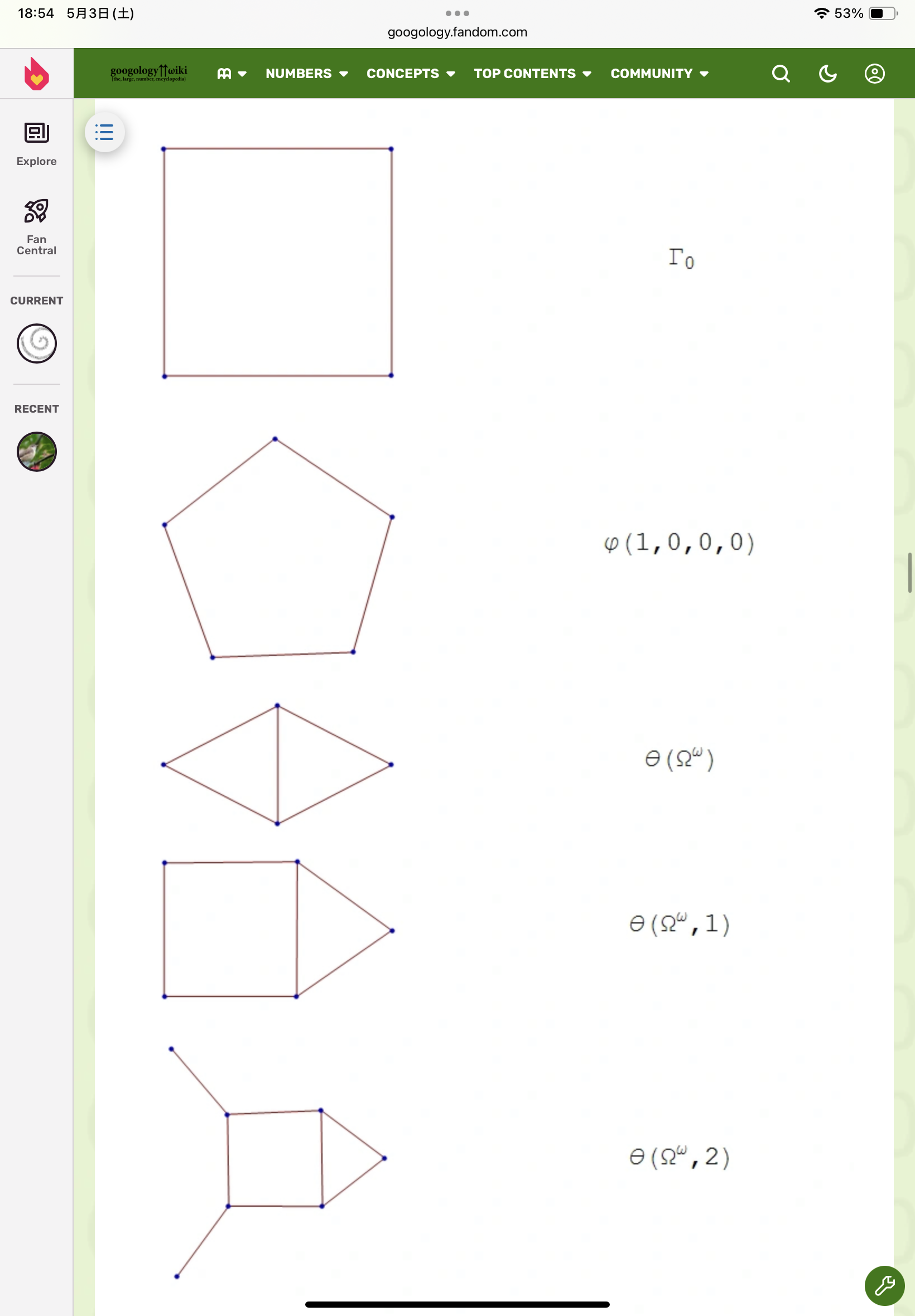順序数3
順序数4
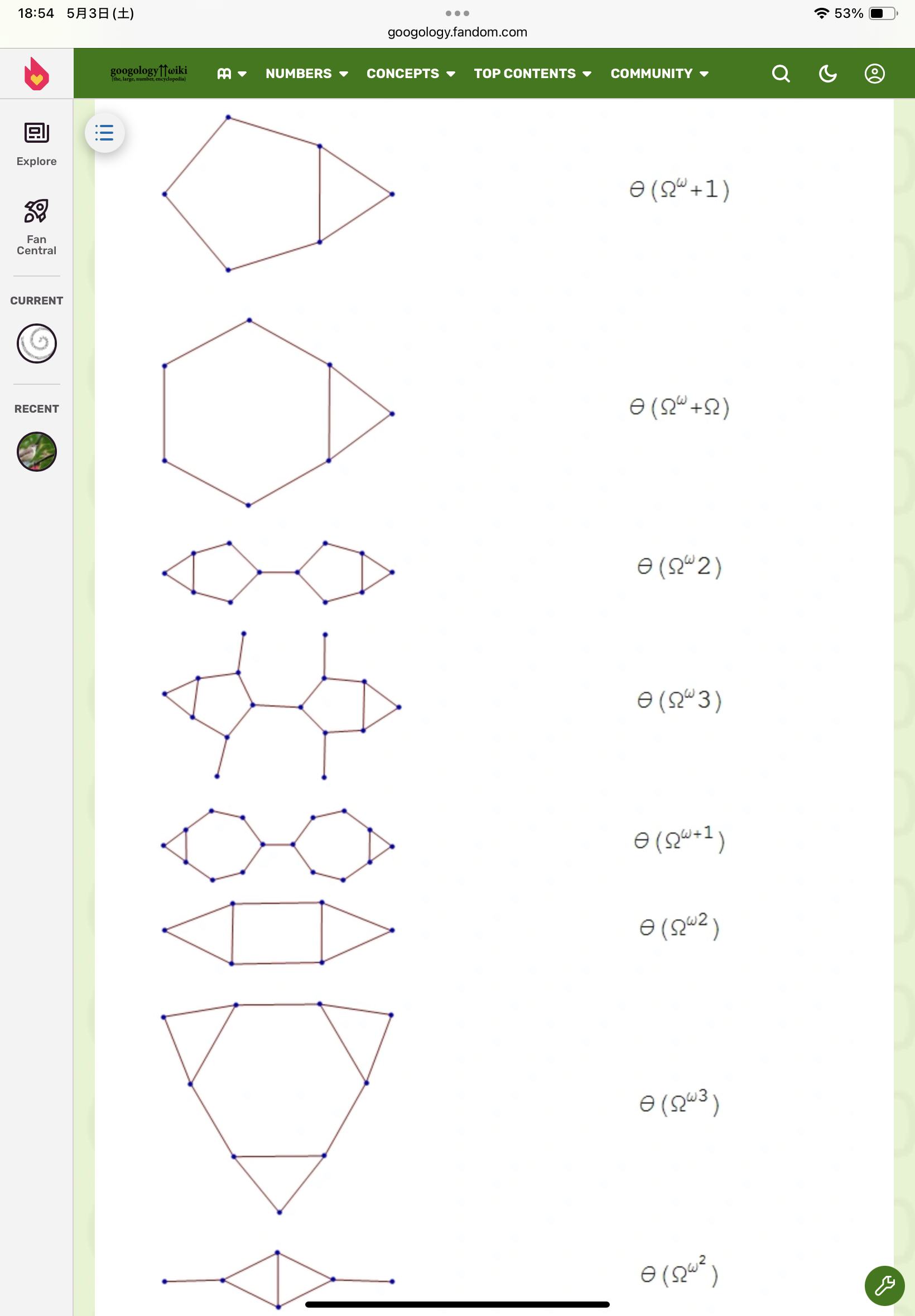
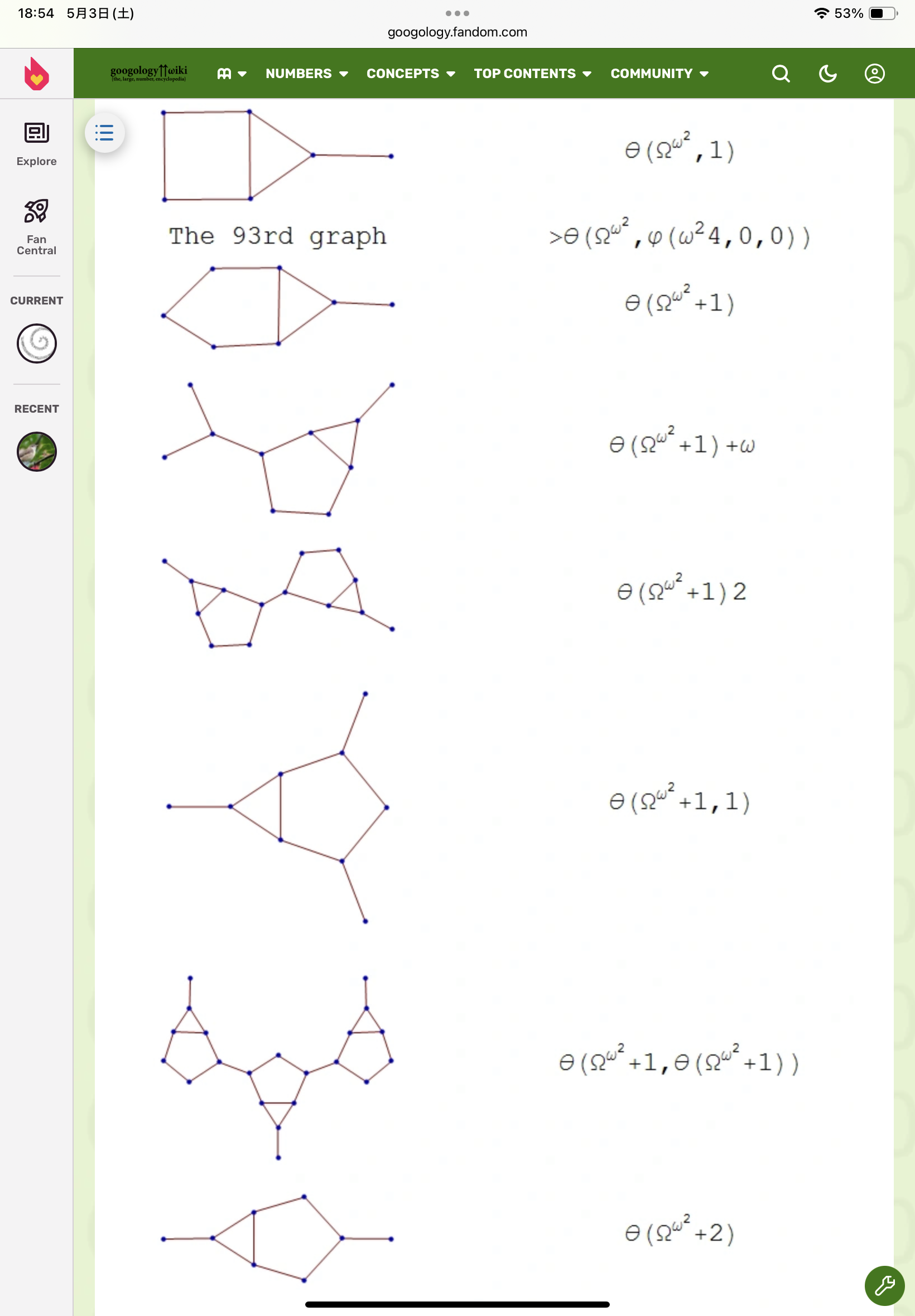順序数5
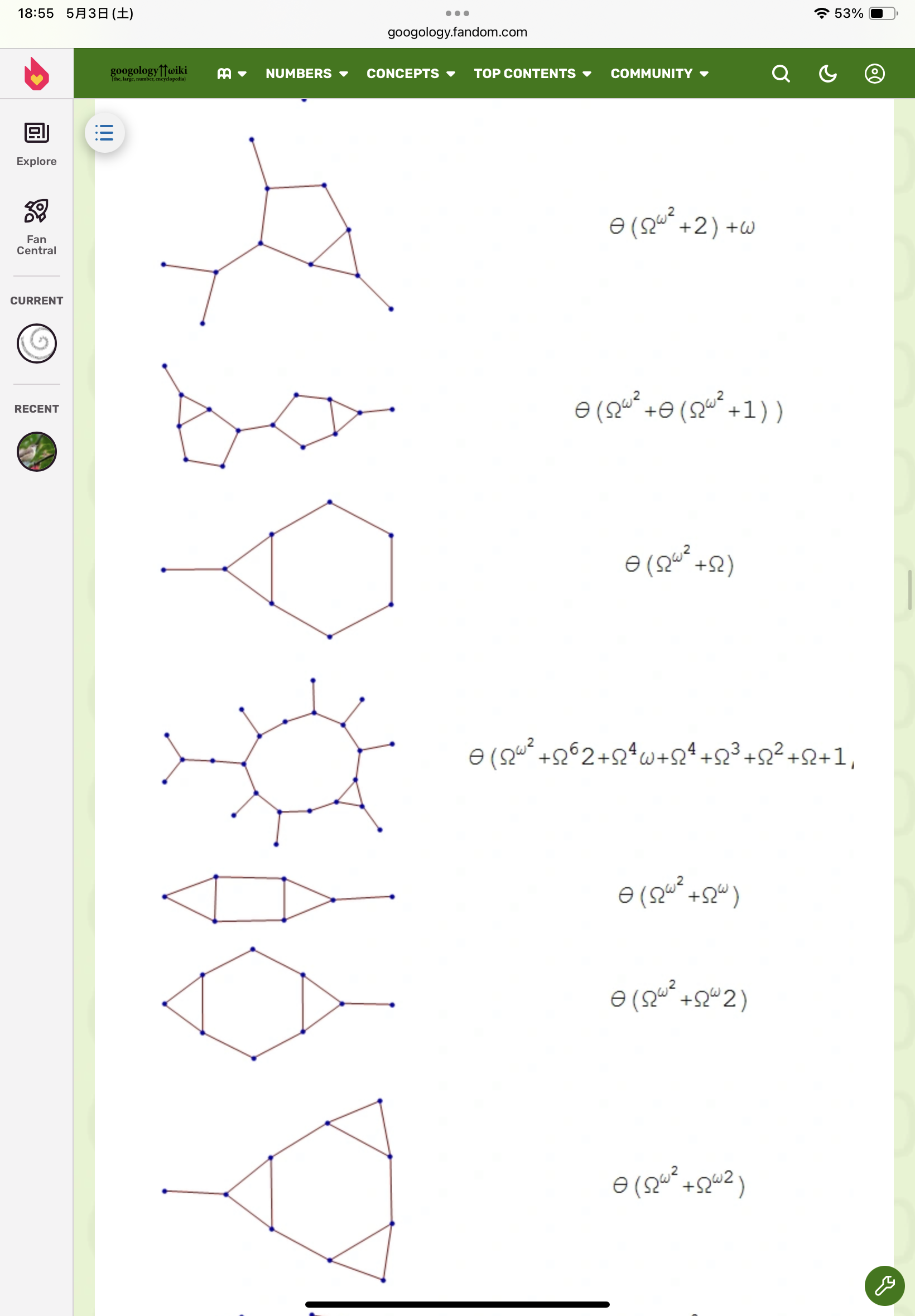順序数6
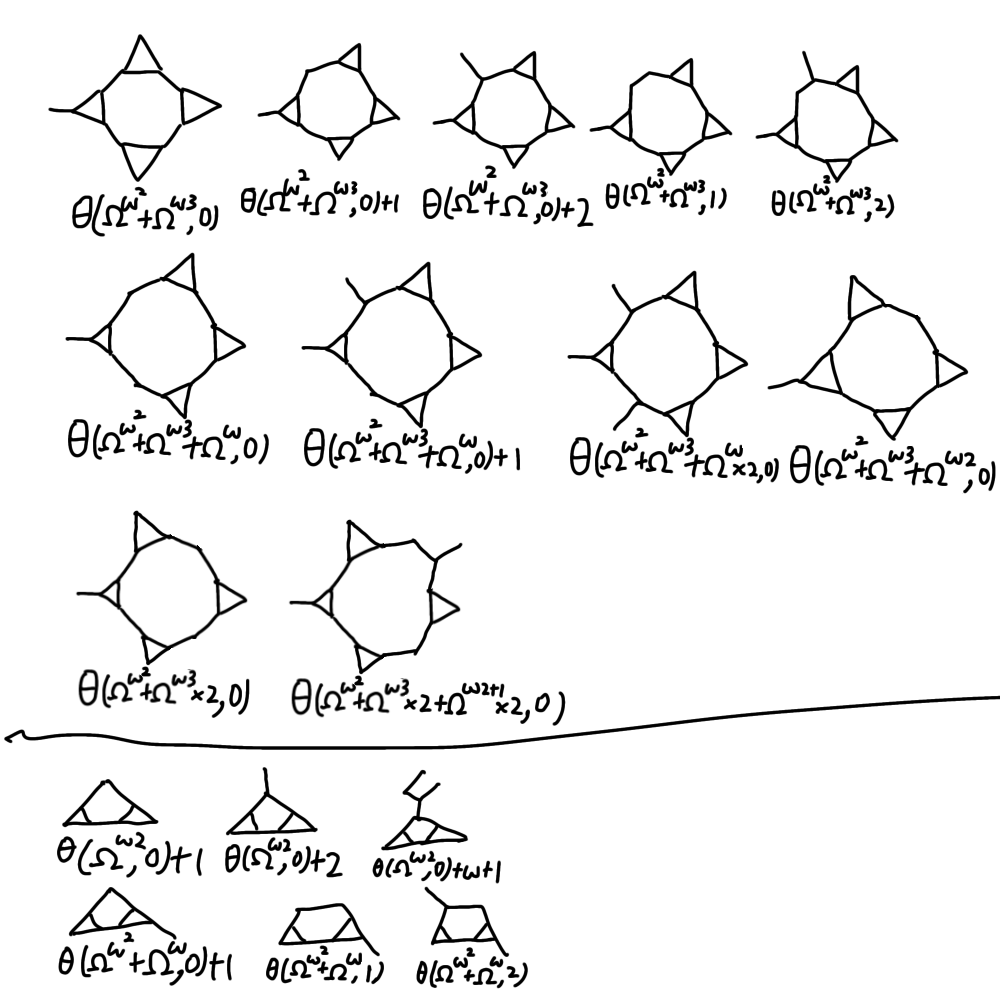新たに用意した順序数
これは従来の近似値より精度が高い。
SSCG(4),SSCG(5)に関するグラフもトークページに記載されている。
SSCG(4)の解析は上手くいかなかったが、
SSCG(5)の解析は上手くいった。
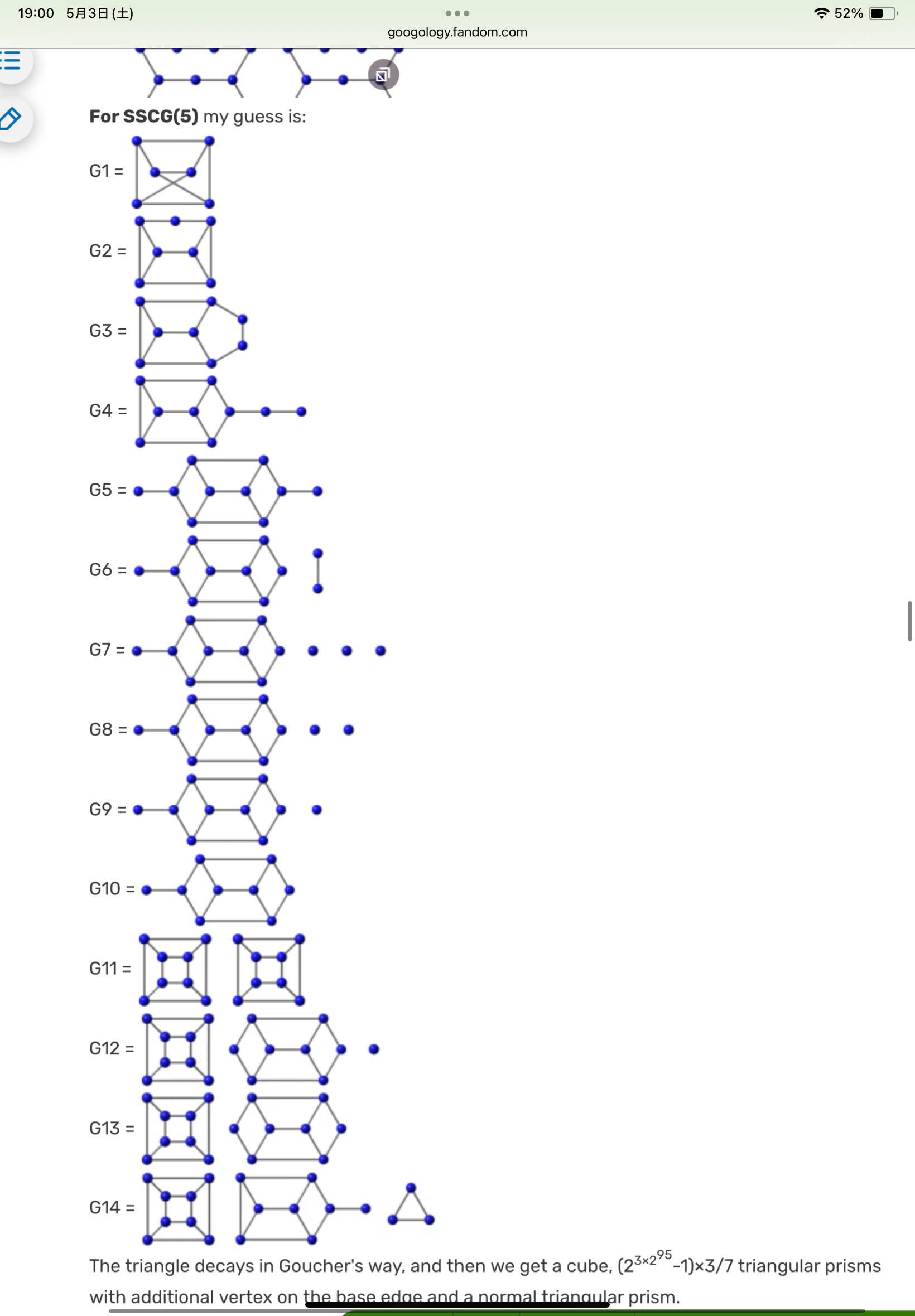SSCG(5)の変形のようす
ここから、新しい順序数を定義しなければならない。
Hyp cosが用意した図形は、θ(Ω_2)未満までであり、それ以降がlevel3に対応すると考えられる。
θ(Ω_2)=Ψ((Ω_2)^(Ω_2))だから、それ以降をブーフホルツのψで近似した。
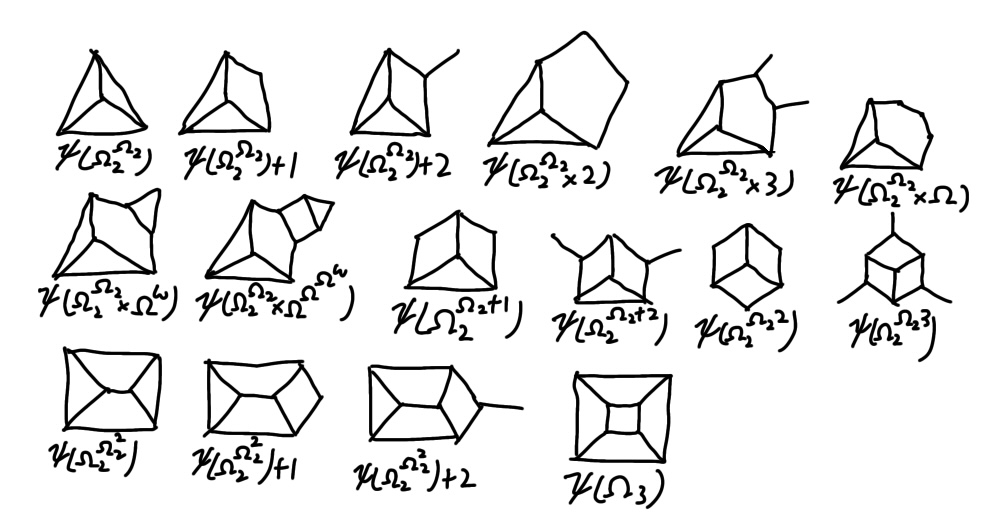新しい順序数
$SSCG(3)>f_{\theta ({\mathrm{\Omega }}^{{\omega }^2}+{\mathrm{\Omega }}^{\omega 3}\times 2+{\mathrm{\Omega }}^{\omega 2+1}\times 2,0)}\left(f_{\theta ({\mathrm{\Omega }}^{{\omega }^2}+{\mathrm{\Omega }}^{\omega },2)}\left(f_{\theta ({\mathrm{\Omega }}^{\omega 2},0)}^2(3\times 2^{3\times 2^{95}})\right)\right)$

$SSCG(5)>f_{\psi ({\mathrm{\Omega }}_3)}\left(f_{\psi \left({\mathrm{\Omega }}_2^{{\mathrm{\Omega }}_2^2}\right)+2}(3\times 2^{3\times 2^{95}})\right)$
BANに直すとこうなる。
SSCG(3)>{3,{3,{3×2^(3×2^95),3,2,[1[1-1,3]2]2}[1[1-1,1,2]1[1-1,2]4]2}[1[1-1,1,2]1[1-1,4]1[1-1,4]1[1-2,3]1[1-2,3]2]2}
SSCG(5)>{3,{3,3×2^(3×2^95),3[1[1[1〜2(/_3)2]2]2]2}[1[1[1(/_3)3]2]2]2}
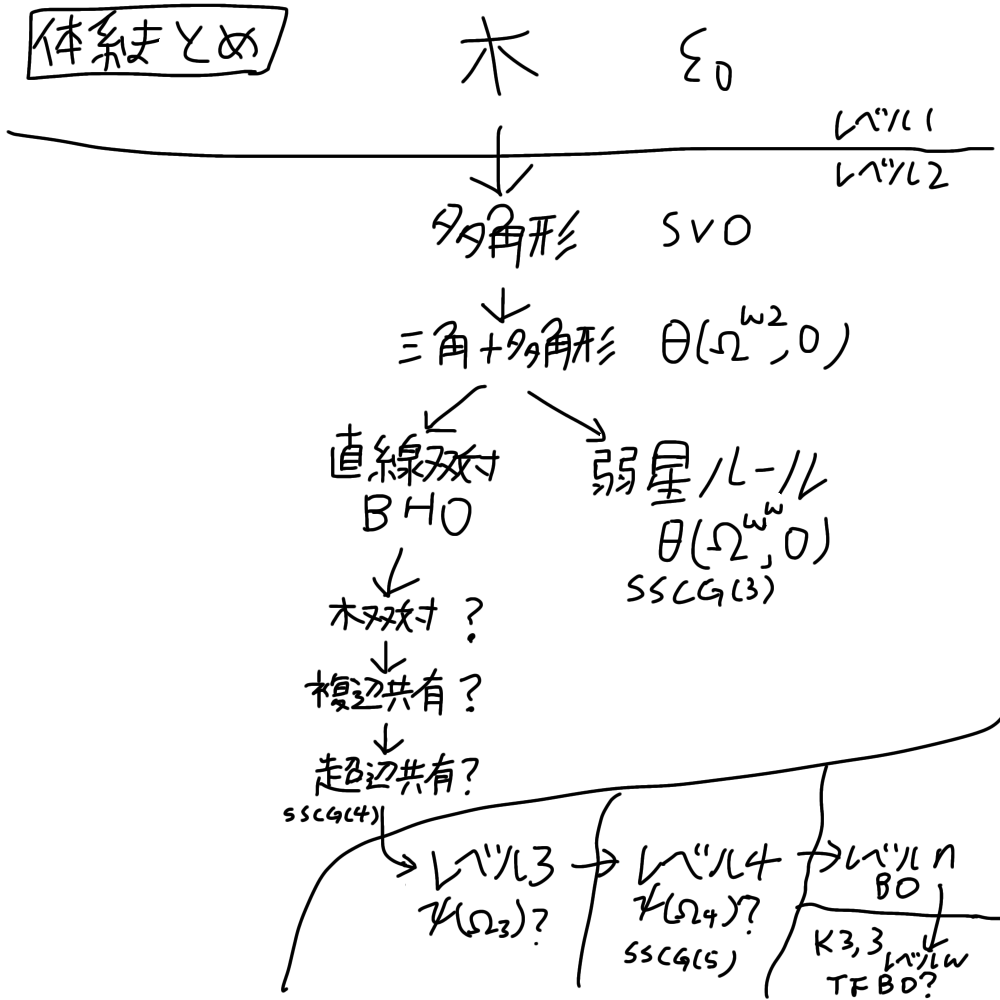体系まとめ
これが、試行錯誤の末私が出した結論だ。
順序数の精度を高めて、さらに効率の良い近似が可能になることが期待されている。
順序数は、各体型の強さの限界を表している。

④SCG数

まず、SCG(0)=6　である。
$SCG(1)>f_{{ϵ}_{2}2}\left(f_{{ϵ}_{0}2}\left(f_{{ϵ}_0+1}\left(f_{{ϵ}_0}\left(f_{{\omega }^{\omega }+1}\left(f_{{\omega }^5+{\omega }^2+\omega }\left(f_{{\omega }^{2}3+1}\left(f_{{\omega }^2+\omega 3+1}\left(f_{{\omega }^2+1}\left(f_{{\omega }^2}(3\times 2^{3\times 2^{95}})\right)\right)\right)\right)\right)\right)\right)\right)\right)$
$SCG(2)>f_{SVO}\left(f_{{ϵ}_{2}2}\left(f_{{ϵ}_{0}2}\left(f_{{ϵ}_0+1}\left(f_{{ϵ}_0}\left(f_{{\omega }^{\omega }+1}\left(f_{{\omega }^5+{\omega }^2+\omega }\left(f_{{\omega }^{2}3+1}\left(f_{{\omega }^2+\omega 3+1}\left(f_{{\omega }^2+1}\left(f_{{\omega }^2}(3\times 2^{3\times 2^{95}})\right)\right)\right)\right)\right)\right)\right)\right)\right)\right)$

これもHyp cosが導びいた結果だ。
バードの配列表記でも近似しておこう。
SCG(1)>f_(ε_2)×2(f_(ε_0)×2(f_(ε_0)+2(2)))
SCG(2)>f_SVO(SCG(1))
より、
SCG(1)>{3,{3,{3,3,3[1/2]2}[1/2]3}[1/4]3}
SCG(2)>{3,{3,{3,{3,3,3[1/2]2}[1/2]3}[1/4]3}[1[1-1,2]2]2}
SCG(3)はどうだろうか。
ある程度大きなnについて、SCG(n)>SSCG(2n+1)+nが証明されている。
n=1,2では成立するとはとても思えないため、n>2で成り立つのではないか。
それを仮定すると、
SCG(3)>SSCG(7)>f_Ψ(Ω_ω)+ω(f_Ψ(Ω_ω)(7))≒{3,{3,7[1[2(/_1,2)2]2]2},1,2,[1[2(/_1,2)2]2]2}>{3,3,2,2,[1[2(/1,2)2]2]2}
という値が得られる。
SCG(4)>SSCG(9)>SSCG(8)>f{\psi ( {\ohm}_\upomega ) +\upomega +2}^{2}( 4)\
≒{3,{3,4,3,2[1[2(/_1,2)2]2]2},3,2[1[2(/_1,2)2]2]2}

{3,3,4,2,[1[2(/_1,2)2]2]2}
これはかなり精度の低い近似だ。
当然、SCG(13)はもっと大きい値になるため、近似は困難である。

⑤SSCG,SCGの関係

実はSSCG,SCGは線形レベルでしか違いがない。
SCG(n)>SSCG(2n+1)+n>SSCG(2n+1)
SSCG(3n+4)>3SCG(n)>SCG(n)
が分かっているからだ。証明は次の通りだ。
上の公式の証明
下の公式の証明
これは何を意味するのか。

よってSSCGとSCGは強さにほとんど違いがない。
私はこの極限が振動するとはとても想定できないため、第一宇野定数と第二宇野定数は一致すると思う。
BOレベルより強いことは既に証明されていて、
Ψ(Ω_ω^ω)より弱いことも分かっているため、TFBレベルだと推測されている。これもある程度の確証がある。それも、CLG理論の産物だ。 K3,3
PSCGに登場せず、SCGに登場する図形はK3,3であり、それが非加算順序数Ω_ωに対応すると考えられているからだ。
それが正しければ、nが十分大きければ
SCG(n)≒SSCG(n)≒f_Ψ(ε_((Ω_ω)+1))(n)となる。

結論

先行研究の式を変形して、
SSCG(n)(n<9),SCG(n)(n<5)の近似に成功した。
ここにのせるのは近似精度が高いものに限定する。
${\displaystyle \begin{array}{l}SSCG(0)=2\\ SSCG(1)=5\\ SSCG(2)=3\times 2^{3\times 2^{95}}-8\\ SSCG(3)>f_{\theta ({\mathrm{\Omega }}^{{\omega }^2}+{\mathrm{\Omega }}^{\omega 3}\times 2+{\mathrm{\Omega }}^{\omega 2+1}\times 2,0)}\left(f_{\theta ({\mathrm{\Omega }}^{{\omega }^2}+{\mathrm{\Omega }}^{\omega },2)}\left(f_{\theta ({\mathrm{\Omega }}^{\omega 2},0)}^2(3\times 2^{3\times 2^{95}})\right)\right)\\ \\ SSCG(5)>f_{\psi ({\mathrm{\Omega }}_3)}\left(f_{\psi \left({\mathrm{\Omega }}_2^{{\mathrm{\Omega }}_2^2}\right)+2}(3\times 2^{3\times 2^{95}})\right)\\ SSCG(7)>f_{\psi (\mathrm{\Omega }\mathrm{\_}\mathrm{\omega })+\mathrm{\omega }}(f_{\psi (\mathrm{\Omega }\mathrm{\_}\mathrm{\omega })}(7))\\ SSCG(8)>f_{\psi (\mathrm{\Omega }\mathrm{\_}\mathrm{\omega })+\mathrm{\omega }+2}^2(4)\\ \\ SCG(-1)=1\\ SCG(0)=6\\ SCG(1)>f_{{ϵ}_{2}2}\left(f_{{ϵ}_{0}2}\left(f_{{ϵ}_0+1}\left(f_{{ϵ}_0}\left(f_{{\omega }^{\omega }+1}\left(f_{{\omega }^5+{\omega }^2+\omega }\left(f_{{\omega }^{2}3+1}\left(f_{{\omega }^2+\omega 3+1}\left(f_{{\omega }^2+1}\left(f_{{\omega }^2}(3\times 2^{3\times 2^{95}})\right)\right)\right)\right)\right)\right)\right)\right)\right)\\ SCG(2)>f_{SVO}\left(f_{{ϵ}_{2}2}\left(f_{{ϵ}_{0}2}\left(f_{{ϵ}_0+1}\left(f_{{ϵ}_0}\left(f_{{\omega }^{\omega }+1}\left(f_{{\omega }^5+{\omega }^2+\omega }\left(f_{{\omega }^{2}3+1}\left(f_{{\omega }^2+\omega 3+1}\left(f_{{\omega }^2+1}\left(f_{{\omega }^2}(3\times 2^{3\times 2^{95}})\right)\right)\right)\right)\right)\right)\right)\right)\right)\right)\\ SCG(3)>f_{\psi (\mathrm{\Omega }\mathrm{\_}\mathrm{\omega })+\mathrm{\omega }}(f_{\psi (\mathrm{\Omega }\mathrm{\_}\mathrm{\omega })}(7))\end{array}}$