２つの図形上の点の距離

円のとき

　私が作問しOMCに出題された以下の問題について考察する。

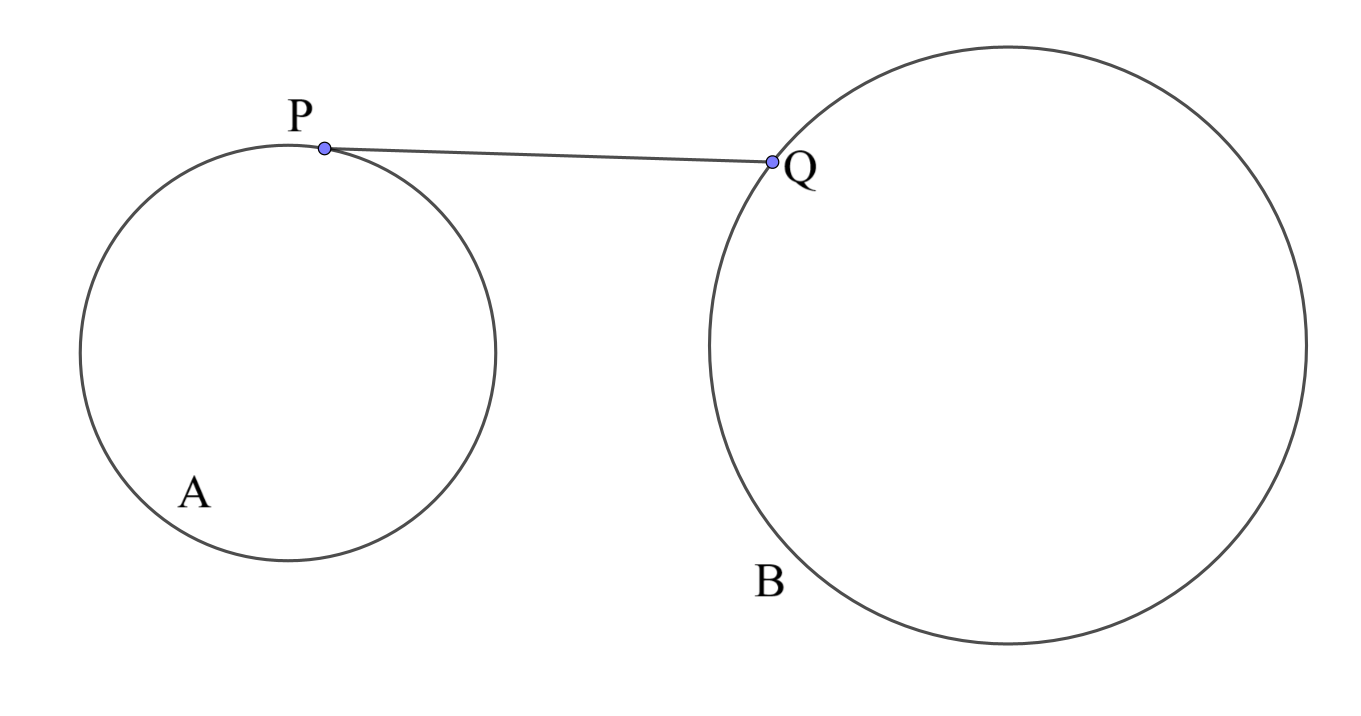
　この記事では、線分$PQ$の長さの最小値と最大値が与えられているということが何を意味するのか考えたい。$2$つの円がどちらも動くのはだるいので、一方の円($A$とする)を固定し、円$B$の存在は一旦忘れる。また、$A$の直径は$300$以下とする。
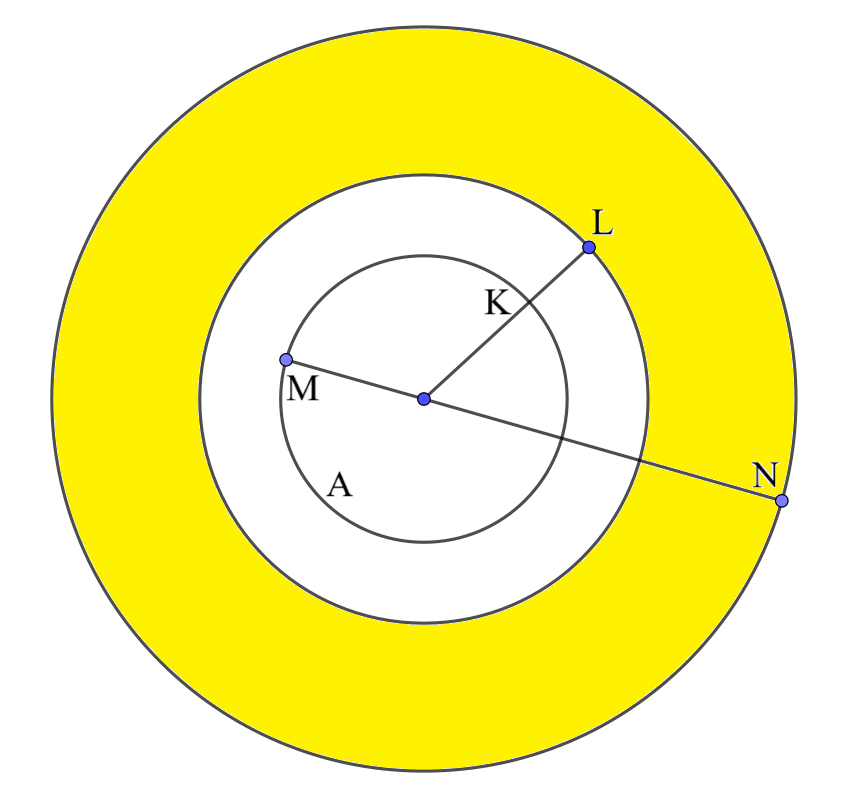
　まず、$A$の周上のある点$K$について、$A$の外部の点$L$を「点$K'$が$A$上を動くとき線分$K'L$の距離の最小値が$10$で、それは$K'=K$のとき実現される」ようにとる。$L$は$A$の中心と$K$を結ぶ直線上であって、$KL=10$を満たす点（のうち$A$の外部にある方）である。
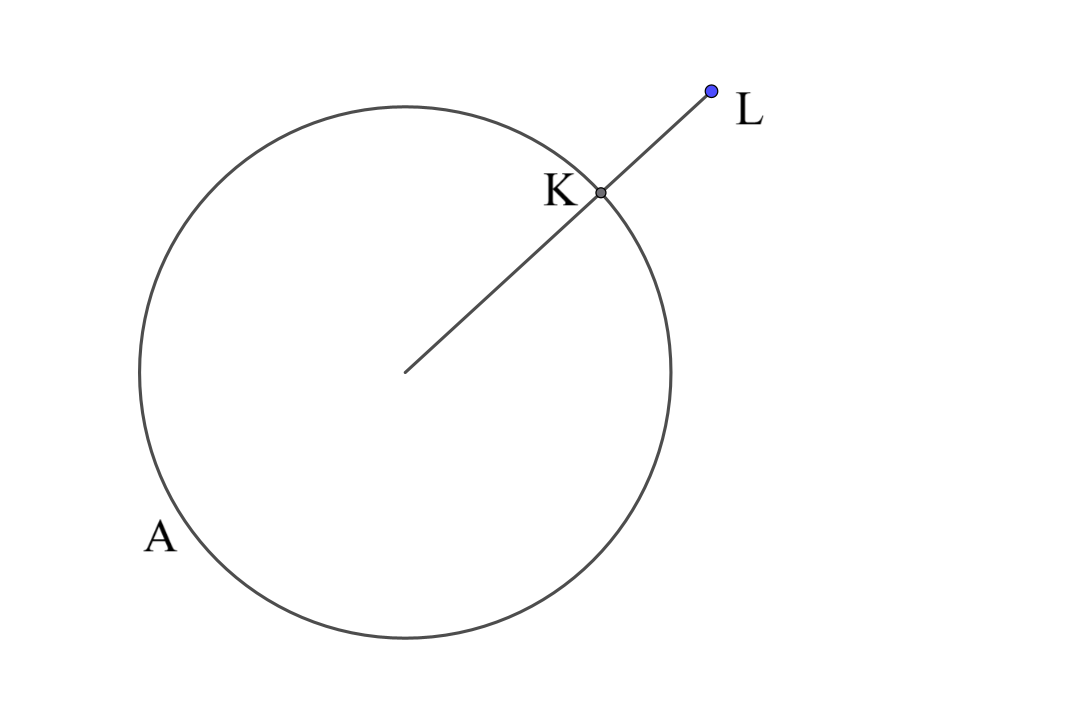幾何あるある、言葉で説明するのはだるいが図はシンプル
$A$上のすべての点に対して$L$にあたる点を取ると、円ができる。つまり、この円周上のどの点についても、「$A$上を動く点との距離の最小値が$10$である」が成り立つ。逆に、「$A$上を動く点との距離の最小値が$10$である」点は、この円周上にある（わけではない。$A$の内部にもそういう点はある。けど、そのへん書くのだるいから許して）。

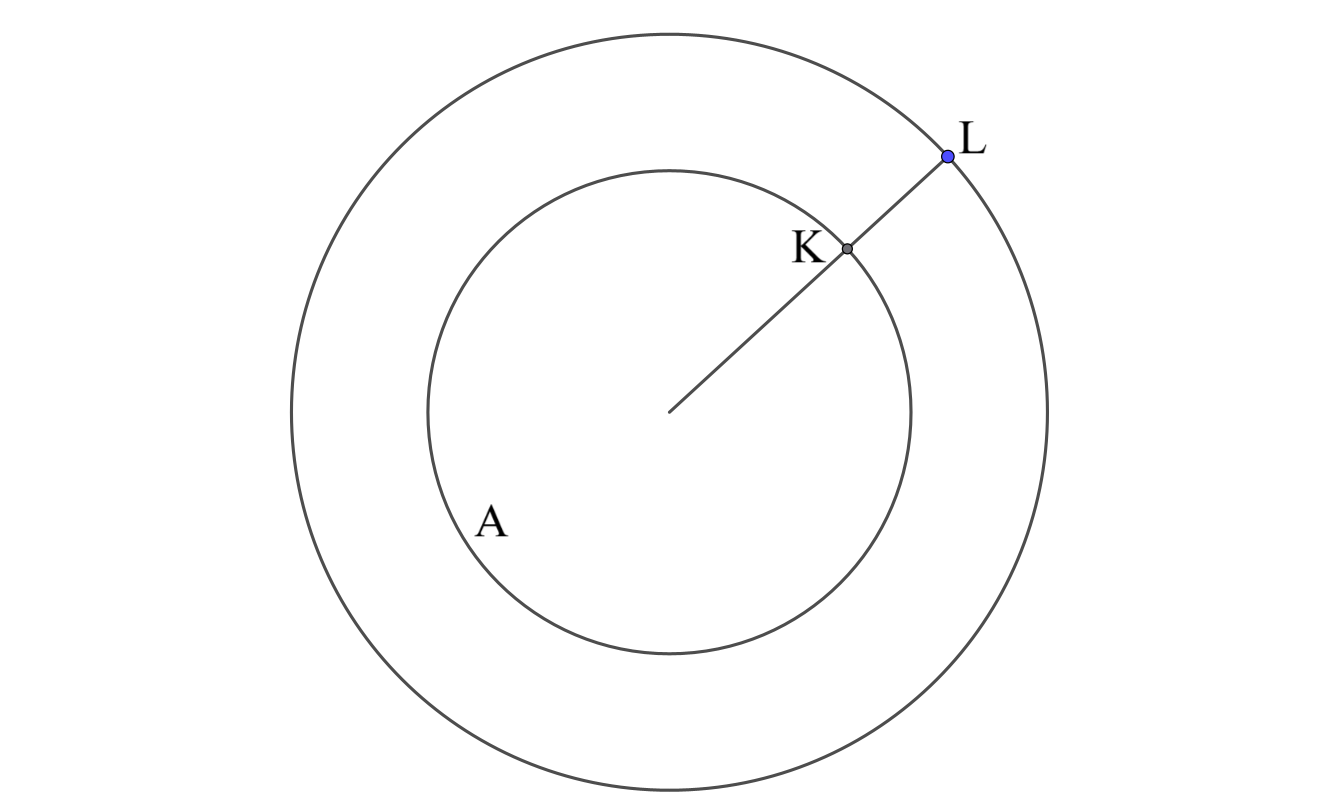
次に、最大値の方を考える。$A$の周上のある点$M$について、$A$の外部の点$N$を「点$M'$が$A$上を動くとき線分$M'N$の距離の最大値が$300$で、それは$M'=M$のとき実現される」ようにとる。$N$は$A$の中心と$M$を結ぶ直線上であって、$MN=300$を満たす点（のうち$A$に近い方）である。

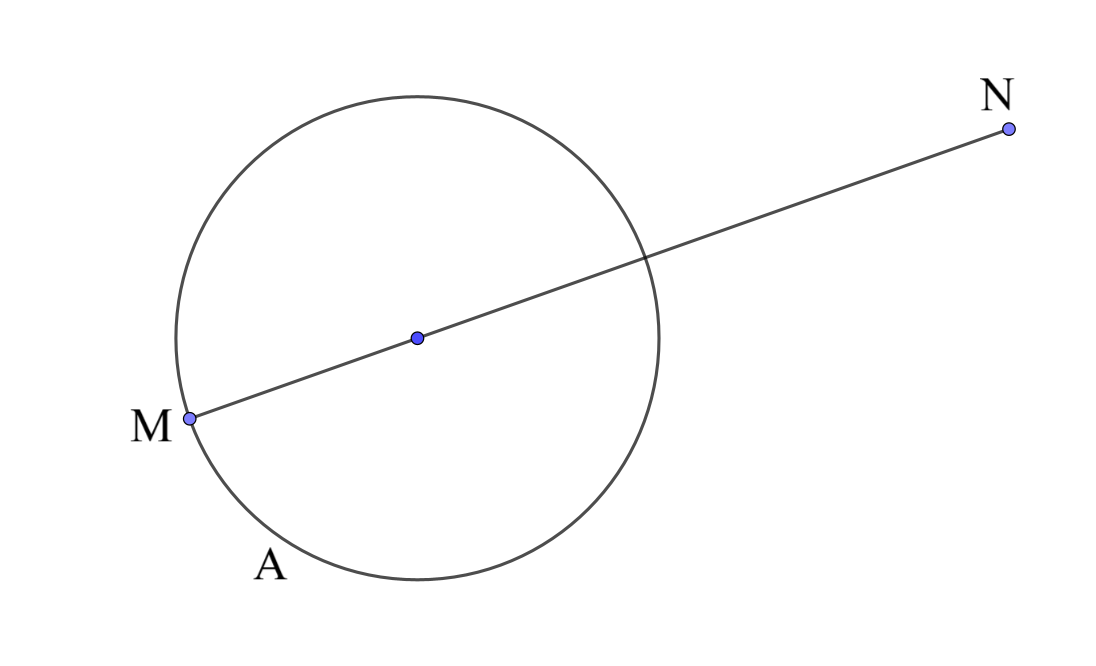
先ほどと同様に、$A$上のすべての点に対して$N$にあたる点を取ると、円ができる。つまり、この円周上のどの点についても、「$A$上を動く点との距離の最大値が$300$である」が成り立つ。逆も成り立つ。
　最小値による円($L$の円)と最大値による円($N$の円)によって囲まれる領域内の点は、$A$の周上の点との距離が$10$以上$300$以下となる。

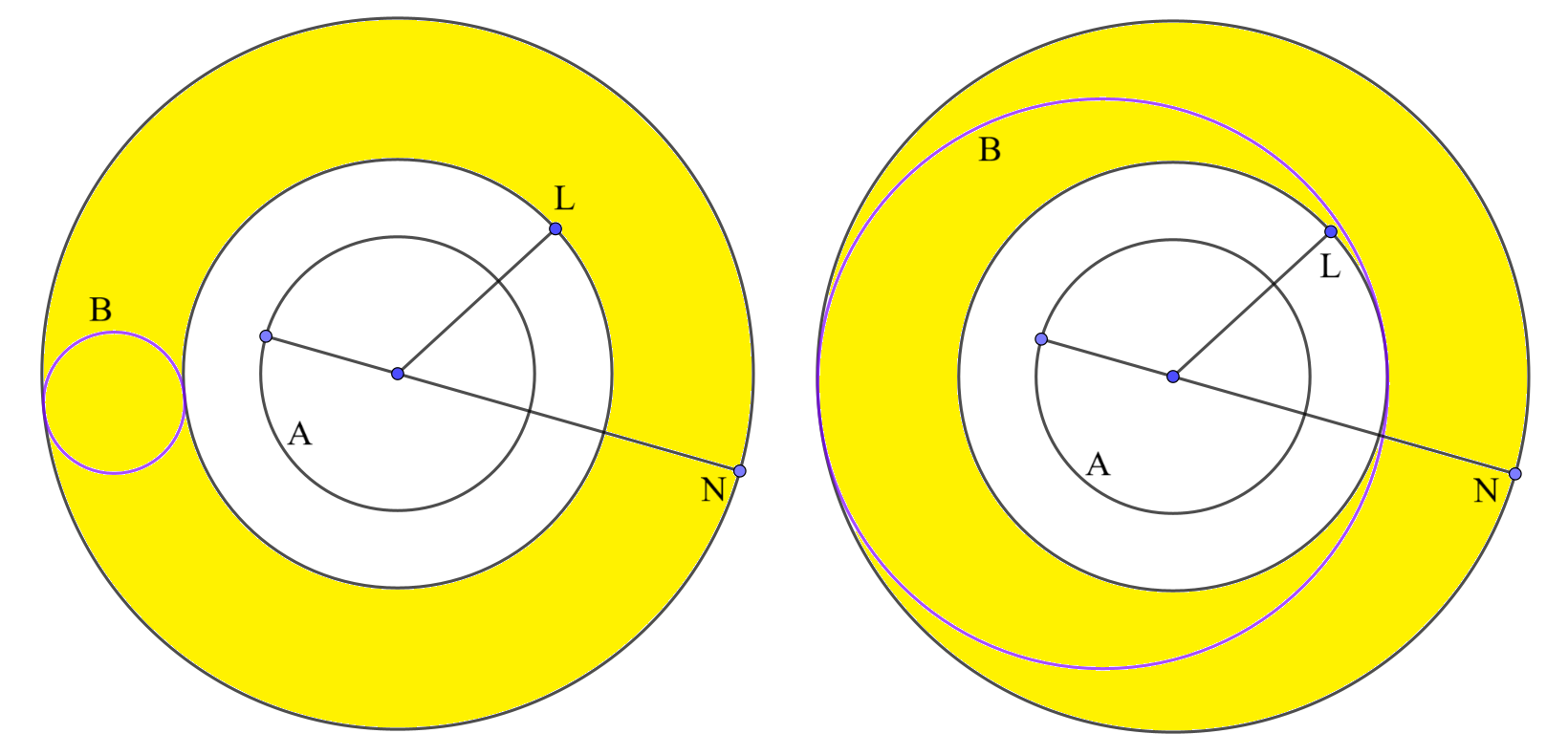
さて、ようやく円$B$について考えるときがきた。$B$の周はこの領域内に存在し、領域の境界($2$つの円)と共有点を持たなければならない。そのような円は、$L$の円との接し方で次の$2$通りがある。OMCの解説の$2$通りの場合分けと同じである。

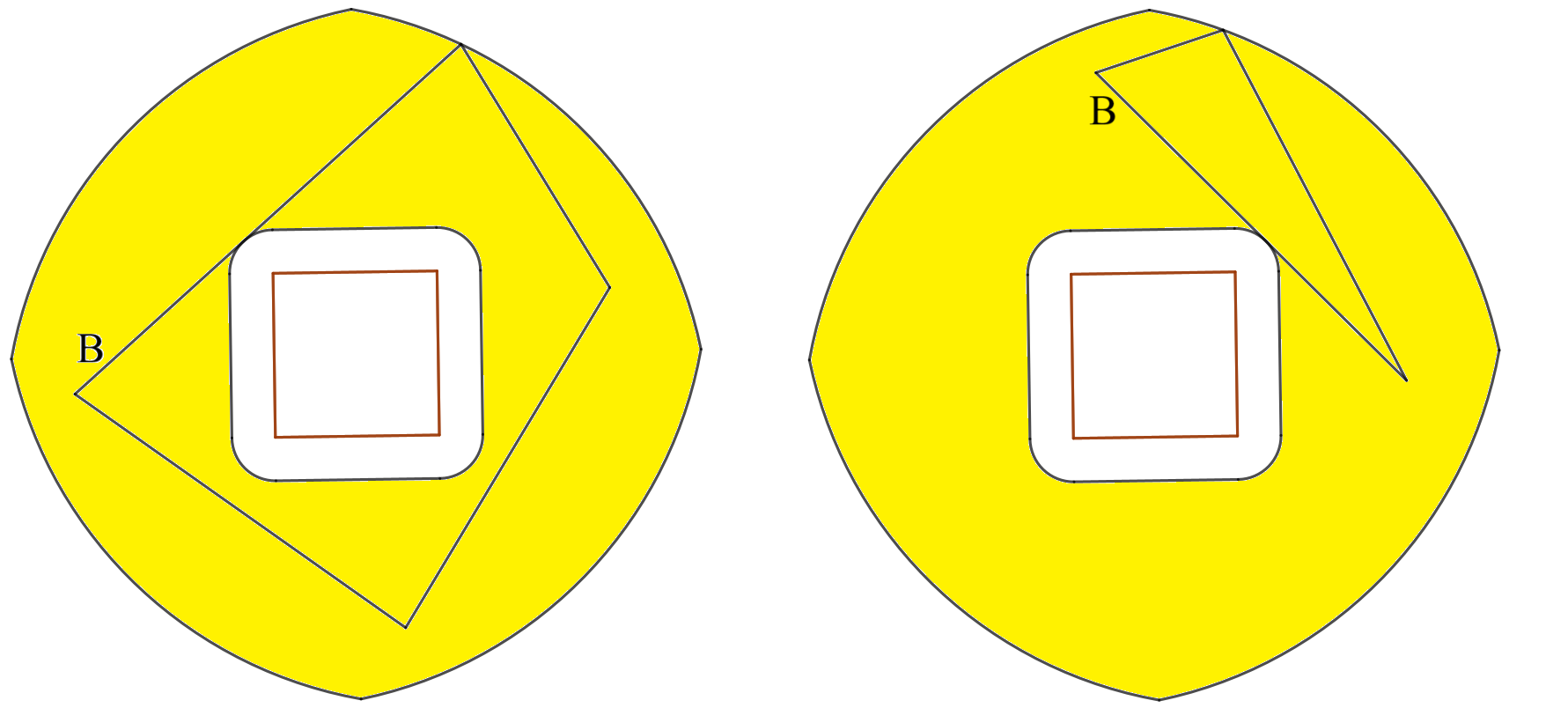
　この黄色の領域を使えば、円$B$の代わりに他の図形を考えることもできる。例えば、以下の図形$B$はどちらも「$A$の周上の点と$B$の周上の点との距離の最小値が$10$で最大値が$300$」を満たす。
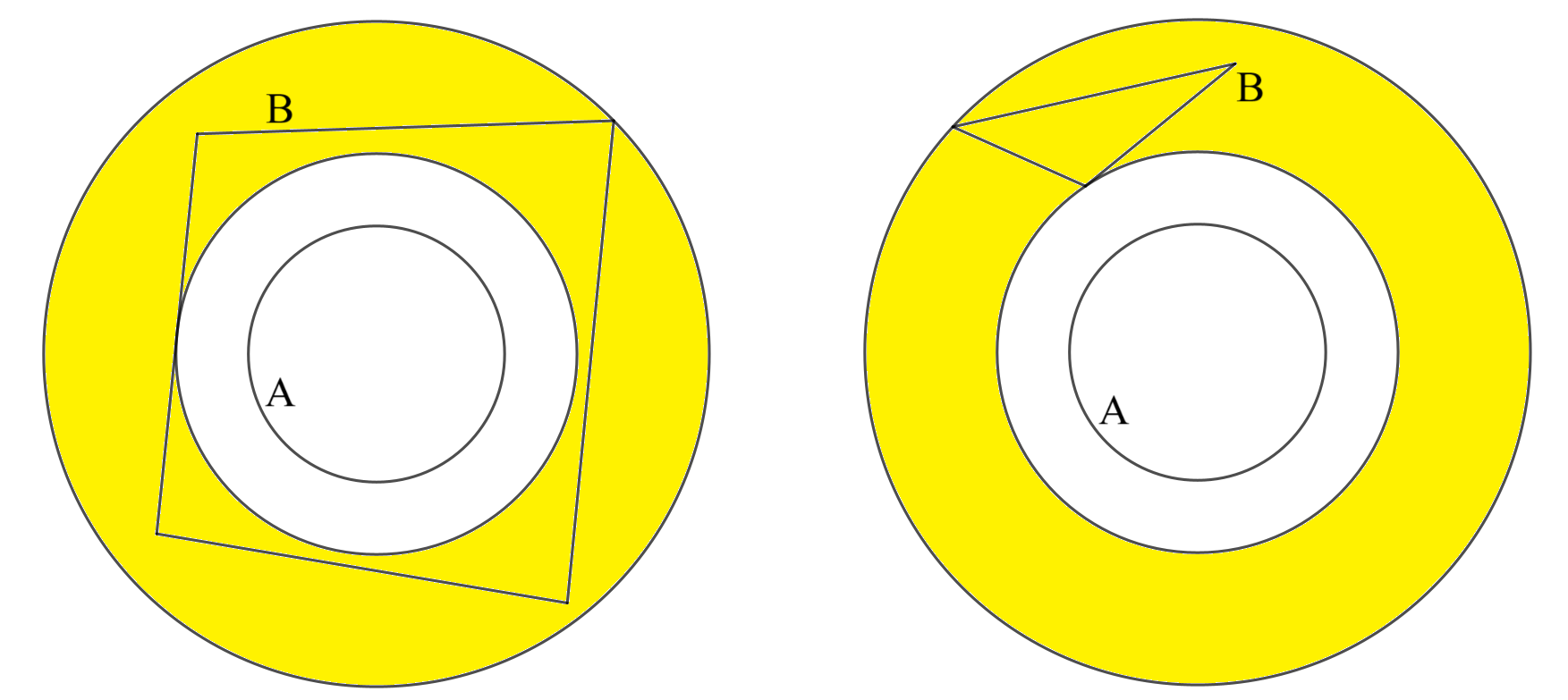四角形、三角形を描いてみた

　ちなみに、$A$の直径が$310$以上のときは内部に領域ができるが、やることは同じなので省略。

正方形のとき

　同様にして、$2$つの図形上の点の距離の最小値($p$とする)と最大値($q$とする)が与えられたとき、一方の図形を固定し、ある領域を作図することでもう一方の図形がどのような条件を満たすかを考えることができそうである。先ほどは円を固定したが、正方形を固定すると次のような領域ができる。

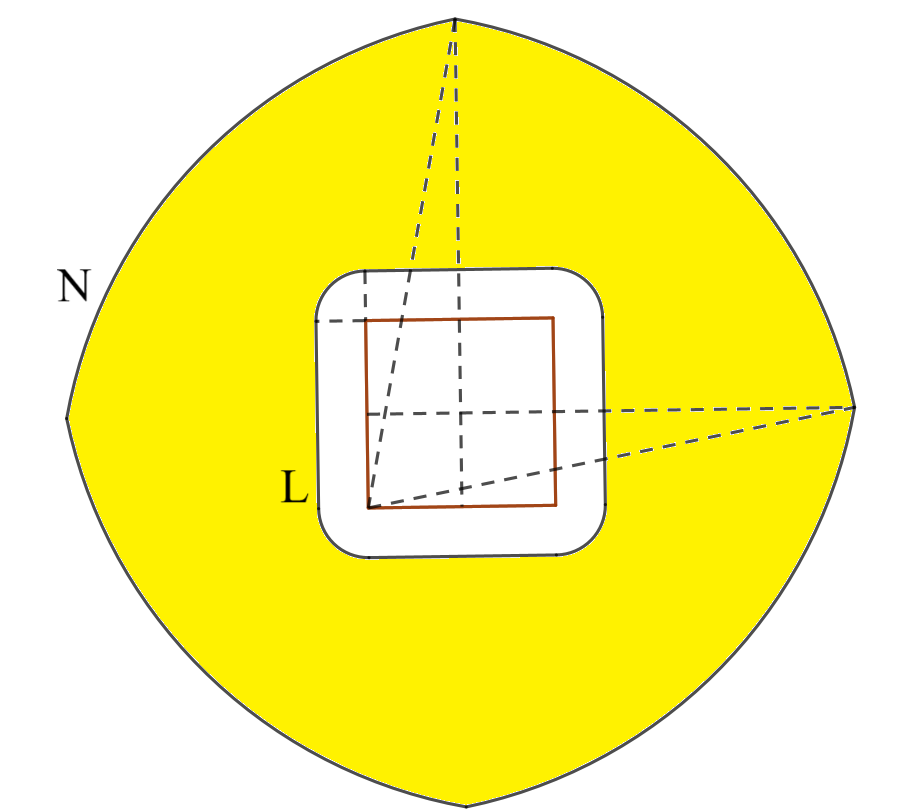
曲線$L$は、正方形の辺に平行な線分と、正方形の頂点を中心とする半径$p$の円弧を繋いだものである。曲線$N$は、正方形の頂点を中心とする半径$q$の円弧を$4$つ繋いだものである。
　黄色の領域に周が含まれ、領域の境界(外側と内側の$2$つ)と共有点を持つ図形$B$を描けば、正方形の周上の点と$B$の周上の点との距離の最小値が$p$、最大値が$q$となる。
四角形、三角形を描いてみた

終

　いろんな図形でお絵描きすると楽しそう。