Airy関数の一般化1:一般化されたAiryの微分方程式と級数解
前書き
一年ほど前に書いた現在非公開になっている記事のリメイクとして、複数の記事に分けてAiry関数の一般化について書くことにしました。
この記事では微分作用素は$D$で表します。
また、複素変数のグラフは白い所ほど絶対値が大きく、彩度が高い場所ほど絶対値が小さいです。
Airy関数とは
Airy関数とは、Airyの微分方程式
$$D^2y=xy$$
の解として定義される関数です。
通常、$s\in\mathbb{R}$に対して第一種Airy関数と第二種Airy関数を次のように定めます。
$$\Ai{s}=\frac{1}{\pi}\int_0^\infty \cos\left(\frac{x^3}{3}+sx\right)dx$$
$$\Bi{s}=\frac{1}{\pi}\int_0^\infty e^{-x^3/3+sx}dx+\frac{1}{\pi}\int_0^\infty\sin\left(\frac{x^3}{3}+sx\right)dx$$
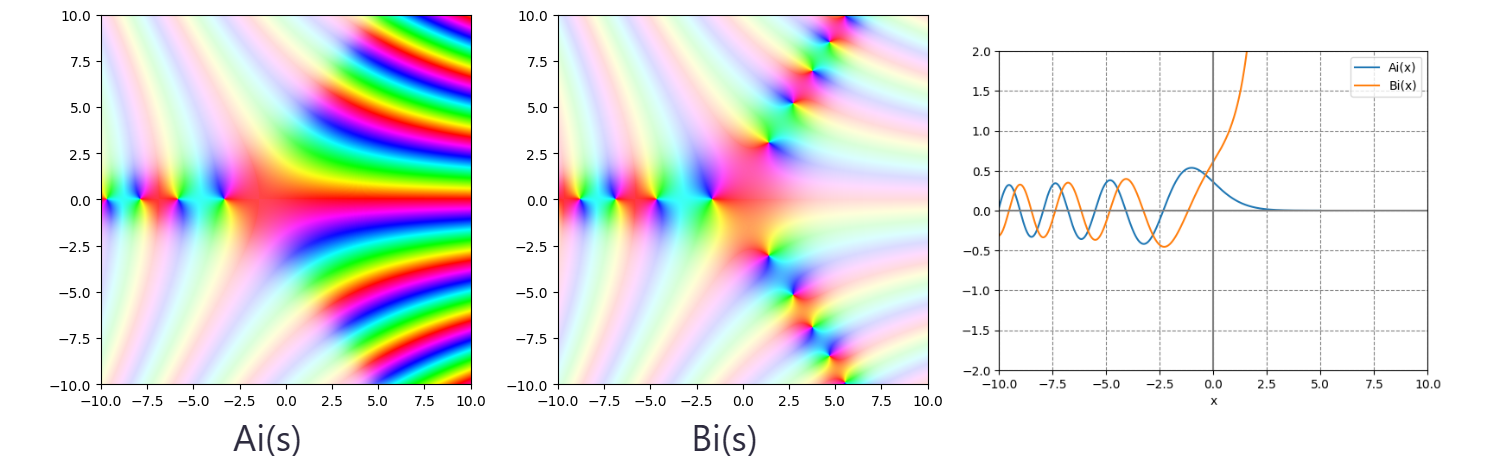 複素変数と実変数のAiry関数
複素変数と実変数のAiry関数
Airy関数はそれ自体とても興味深い関数です。いつかAiry関数に関する記事も書いてみたいですね。
一般化されたAiryの微分方程式
$\mu,\nu\in\mathbb{N}^*$に対して、一般化されたAiryの微分方程式$\Om{\mu}{\nu},\Ombar{\mu}{\nu}$を次のように定めます。
$$\Om{\mu}{\nu}:D^\mu y=x^\nu y$$
$$\Ombar{\mu}{\nu}:D^\mu y=-x^\nu y$$
$\mu,\nu$をそれぞれこの方程式の階数、次数と呼び、$\omega=\mu+\nu$を重さと呼ぶことにします。
$\mu=2,\nu=1$で通常のAiryの微分方程式に一致しますね。
定義で$\mu,\nu$をこの範囲に限定したのは、次の記事で解説する手法をうまく適応するためです。
$\nu\in\mathbb{C}$に対して考えるときも同じように$\Om{\mu}{\nu},\Ombar{\mu}{\nu}$と記すことにします。
・$\mu=0$
$\nu=0$のときあらゆる関数が解になり、そうでないとき$y=0$以外の解を持ちません。
定義から除外して正解ですね。
・$\nu=0$
これは指数関数で解を表すことができます。これらの解をcol関数と呼ぶこともあるようです。
これらも例外的にふるまうので、定義から除外しています。
・$\mu=1$
ここで紹介する例の中で最も重要です。
$\Om{1}{\nu}:Dy=x^\nu y$ですから、解は$ce^{x^\omega/\omega}$($c$は定数)となります。
同様に、$ce^{-x^\omega/\omega}$が$\Ombar{1}{\nu}$の解です。
三つ目の例は次回の要になります。
初等関数で表せる例はこれらが全てだと思っています(微分Galois理論なんかを使えば証明出来るのでしょうか…?)
以降、関数$y$がある微分方程式$E$の解であることを単に$y\in E$と書きます。
一般化超幾何級数を使った解
ひとまず、すべての解を得たいです。これは可能で、一般化超幾何級数で表すことができます。
ここでは$\nu\in\mathbb{C}$を許します。
$0\leq m<\mu$に対して、$\mu-1$の数を持つ$\mu$個のベクトルパラメータ$\omega_m$を次のように定義します。
$$\omega_0=\left(1-\frac{\mu-1}{\omega},1-\frac{\mu-2}{\omega},...,1-\frac{2}{\omega},1-\frac{1}{\omega}\right)$$
$$\omega_1=\left(1-\frac{\mu-2}{\omega},...,1-\frac{2}{\omega},1-\frac{1}{\omega},1+\frac{1}{\omega}\right)$$
...
$$\omega_m=\left(1-\frac{\mu-(m+1)}{\omega},...,1-\frac{1}{\omega},1+\frac{1}{\omega},...,1+\frac{m}{\omega}\right)\;\;\;\;\;\;(m\neq0,\mu-1)$$
...
$$\omega_{\mu-1}=\left(1+\frac{1}{\omega},1+\frac{2}{\omega},...,1+\frac{\mu-2}{\omega},1+\frac{\mu-1}{\omega}\right)$$
これを用いて解を構成することができます!
$x\in\mathbb{C}$に対して、関数$\Om{}{\mu\nu m},\Ombar{}{\mu\nu m}$を次のように定義します。
$$\Om{}{\mu\nu m}(x)=\frac{x^m}{m!}\hyF{0}{\mu-1}{-}{\omega_m}{\frac{x^\omega}{\omega^\mu}}$$
$$\Ombar{}{\mu\nu m}(x)=\Om{}{\mu\nu m}(e^{\pi i/\omega}x)$$
$\nu=0$でcol関数の定義一致することは、ガンマ関数の倍数公式を使えばわかります。
また、$\mu=1$で先ほど例にあげた関数になることもわかりますね。
次の定理は、これらの関数がある意味でもっとも基本的な解となっていることを主張しています。
$\Om{}{\mu\nu m},\Ombar{}{\mu\nu m}\;\;(m=0,...,\mu-1)$は$\Om{\mu}{\nu},\Ombar{\mu}{\nu}$の解となる。
さらに、次のなりたつ:
$$\Om{(k)}{\mu\nu m}(0)=\delta_{mk}$$
よって、これらの関数の線形結合が一般解となる。
解になっている事の証明
ここで$(\omega_m)_n$はパラメータ内の数のPocchammer記号をすべて掛け合わせたものとします。
$$\Omega_{\mu\nu m}(x)=\frac{x^m}{m!}{}_{0}F_{\mu-1}\left[\begin{matrix}-\\\omega_m\end{matrix};\frac{x^\omega}{\omega^\mu}\right]
=\sum_{n=0}^{\infty}\frac{x^{\omega n+m}}{n!m!\omega^{\mu n}(\omega_m)_n}
$$
これを$\mu$回微分します。
$$\begin{align*}D^{\mu}\sum_{n=0}^{\infty}\frac{x^{\omega n+m}}{n!m!\omega^{\mu n}(\omega_m)_n}
&=\sum_{n=0}^{\infty}\frac{x^{\omega n+m-\mu}}{n!m!\omega^{\mu n}(\omega_m)_n}\frac{(\omega n+m)!}{(\omega n+m-\mu)!} \\
&=\sum_{n=0}^{\infty}\frac{x^{\omega (n-1)+m+\nu}}{n!m!\omega^{\mu n}(\omega_m)_n}\frac{(\omega n+m)!}{(\omega (n-1)+m+\nu)!}
\end{align*}$$
ここで$n=0$のとき、$m+\nu<\omega$で$m,\mu$は正の整数なので$1/(-\omega+m+\nu)!=0$です。
よって、最初の項は消えて次のようになります。
$$\begin{align*}\sum_{n=0}^{\infty}\frac{x^{\omega (n-1)+m+\nu}}{n!m!\omega^{\mu n}(\omega_m)_n}\frac{(\omega n+m)!}{(\omega (n-1)+m+\nu)!} &=x^\nu\frac{x^m}{m!}\sum_{n=1}^{\infty}\frac{x^{\omega (n-1)}}{n!\omega^{\mu n}(\omega_m)_n}\frac{(\omega n+m)!}{(\omega (n-1)+m+\nu)!}\\
&=x^\nu\frac{x^m}{m!}\sum_{n=0}^{\infty}\frac{x^{\omega n}}{(n+1)!\omega^{\mu (n+1)}(\omega_m)_{n+1}}\frac{(\omega n+m+\omega)!}{(\omega n+m+\nu)!}\\
&=x^\nu\frac{x^m}{m!}\sum_{n=0}^{\infty}\frac{x^{\omega n}}{n!\omega^{\mu n}(\omega_m)_{n}}\frac{(\omega n+m+\omega)!}{(n+1)\omega^\mu(\omega_m+n)(\omega n+m+\nu)!}\\
\end{align*}$$
ここで$\omega_m+n$は$\left(1-\frac{\mu-(m+1)}\omega+n\right)...\left(1-\frac{1}\omega+n\right)\left(1+\frac{1}\omega+n\right)...\left(1+\frac{m}\omega+n\right) $のように、
$\omega_m$のすべての成分に$n$を足したものの積です。
これによって、
$$\frac{(\omega n+m+\omega)!}{(n+1)\omega^\mu(\omega_m+n)(\omega n+m+\nu)!}=1$$
が成立していればいいことが分かります。$\omega_m$が$\mu-1$個の数を持つことに注意すれば、
$$\begin{align*}\omega^\mu(n+1)(\omega_m+n)&=\omega^\mu(n+1)\left(1-\frac{\mu-(m+1)}\omega+n\right)...\left(1-\frac{1}\omega+n\right)\left(1+\frac{1}\omega+n\right)...\left(1+\frac{m}\omega+n\right)\\
&=(\omega n+\omega)(\omega-\mu+(m+1)+\omega n)...(\omega-1+\omega n)(\omega+1+\omega n)...(\omega+m+\omega n)\\
&=(\omega n+\omega+(m+1)-\mu)...(\omega n+\omega-1)(\omega n+\omega)(\omega n+\omega+1)...(\omega n+\omega+m)\\
&=\frac{(\omega n+\omega +m)!}{(\omega n+\nu +m)!}
\end{align*} $$
よって求めていた式は成立しているため、$\Omega_{\mu\nu m}(x)$は$\Omega^\mu_\nu$の解になっています。
厳密には$m=0,\mu-1$の時は場合分けしなければいけませんが全く同様に示せるので省略しています。
$\bar{\Omega}^\mu_\nu$の解については$\Omega_{\mu\nu m}(e^{\pi i/\omega}x)$を普通に$\mu$回微分すればわかります。
$\Om{(k)}{\mu\nu m}(0)=\delta_{mk}$の証明
$$\begin{align*}\Omega^{(k)}_{\mu\nu m}(0)&=D^{k}\sum_{n=0}^{\infty}\frac{x^{\omega n+m}}{n!m!\omega^{\mu n}(\omega_m)_n} \\
&=\sum_{n=0}^{\infty}\frac{x^{\omega n+m-k}}{n!m!\omega^{\mu n}(\omega_m)_n}\frac{(\omega n+m)!}{(\omega n+m-k)!} \\
\end{align*}$$
ここで、$m$と$k$の大小関係で場合分けします。
・$m>k$
この場合$m-k$は正の整数になるので、それを$n_+$と書くことにします。この場合、
$$
\Omega^{(k)}_{\mu\nu m}(x)
=\sum_{n=0}^{\infty}\frac{x^{\omega n+n_+}}{n!m!\omega^{\mu n}(\omega_m)_n}\frac{(\omega n+m)!}{(\omega n+n_+)!} =\frac{x^{n_+}}{n_+!}+o(x^{\omega+n_+})
$$
となるので$\Omega^{(k)}_{\mu\nu m}(0)=0$となります
・$m< k$
この場合$m-k$は負の整数になるので、それを$n_-$と書くことにします。最初の項が$1/n_-!=0$のおかげで消えることに注意すれば、
$$
\Omega^{(k)}_{\mu\nu m}(x)
=\sum_{n=0}^{\infty}\frac{x^{\omega n+n_-}}{n!m!\omega^{\mu n}(\omega_m)_n}\frac{(\omega n+m)!}{(\omega n+n_-)!} =\frac{x^{\omega+n_-}}{(\omega+n_-)!}+o(x^{2\omega+n_-})
$$
となるのでこの場合も$\Omega^{(k)}_{\mu\nu m}(0)=0$となります
・$m=k$
最後の場合です。$m-k=0$なので、
$$
\Omega^{(k)}_{\mu\nu m}(x)
=\sum_{n=0}^{\infty}\frac{x^{\omega n}}{n!m!\omega^{\mu n}(\omega_m)_n}\frac{(\omega n+m)!}{(\omega n)!} =1+o(x^{\omega})
$$
となります。よって$\Omega^{(k)}_{\mu\nu m}(0)=1$です。
この性質のおかげで、次のように任意の解をシンプルに表示できます。
また、ある解を$0$の周りで定義できれば$\mathbb{C}$全体に解析接続できます。($\nu$が正整数でなければ分岐点を持ちます)
$\Omega\in\Om{\mu}{\nu}$が$0$の周りで定義されているとする。次が成り立つ。
$$\Omega(x)=\sum_{m=0}^{\mu-1}\Omega^{(m)}(0)\Om{}{\mu\nu m}(x)$$
両辺ともに$\Om{\mu}{\nu}$の解になっていて、$\mu-1$階までの導関数の$0$での値が一致するので問題ないですね。
Wronskianもきれいに求めることができます。
$n$個の関数$f_0,f_1,...,f_{n-1}$のWronskianを次のように記すことにします。(かっこいいので)
$$ \newcommand{\opE}{\mathop{\mathcal{W}}}\begin{equation*} \opE_{m=0}^{n-1}f_m(x)\end{equation*} $$
$\mu\neq1$のとき、次が成り立つ。
$$ \newcommand{\opE}{\mathop{\mathcal{W}}}\begin{equation*} \opE_{m=0}^{\mu-1}\Om{}{\mu\nu m}(x)=1\end{equation*} $$
$\mu\neq1$のとき、$\Om{\mu}{\nu}$は$\mu-1$階微分の項を含まないので、Abelの恒等式よりWronakianは定数になります。
よって、$x=0$とすれば得られます。
他にも級数の形から直ちにわかることとして、対称性があります。
$$\Om{}{\mu\nu m}(e^{2\pi i/\omega}x)=e^{2\pi mi/\omega}\Om{}{\mu\nu m}(x)$$
以上が$\Om{}{\mu\nu m}(x)$の基本的な性質です。実際にこれらの関数を観察してみましょう。
具体例
これらは一般Airy関数と呼ばれるクラスの関数になり、Bessel関数で表すことができます。
3つ目の記事で中心的に扱います。
![!FORMULA[109][-1123759433][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F0KweIqJxR28FMfoYl1lb.png?alt=media) $\mu=2,\nu=1,2,3$
$\mu=2,\nu=1,2,3$
![!FORMULA[111][-994676714][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FnXrI9CJsEiRJFgHdqtnT.png?alt=media) $\mu=3,\nu=1,2,3$
$\mu=3,\nu=1,2,3$
![!FORMULA[113][-865593995][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FHH8LIk4b5RR4oFfXEe27.png?alt=media) $\mu=4,\nu=1,2,3$
$\mu=4,\nu=1,2,3$
対称性や零点の位数が見て取れますね。
しかし、どの関数も$+\infty$方向で発散しています!
$\mu=2$のときはかろうじていくつかの方向で消えていますが、それ以上の階数では全方向で発散していていますね...
後書き
これは困りました。第一種Airy関数は実軸上有界なのが重要でした。
積分変換を考えたりするためにも、実軸上有界な関数を得ることが大切です。
次回は、実軸上有界な関数を得る方法を確立し、実際に$\nu=1$の場合に適応していきます。
