特異点論入門〜これほど簡単な入門記事は多分ない〜part6
3次曲線の分類
こんにちは、しんぎゅらです！！
先日(たしか3月くらいだった気がする忘れた...)(忘れるくらい前って先日ではなくない？), 私の所属する数学サークルませまてぃかで数学の発表会がありましたのでその際使用したスライドを公開します
特異点論かと言われれば？？ですが, Dimcaの"Topics on Real and Complex Singularities"に記載されていたのでpart6として書きます(part5はどこ行った？？)(早く書け！！)
また今回の記事は主にpart2の内容を前提としているので、part2にお立ち寄りください
必要な定義
$\On=E_{3,1}$:正則関数芽全体とします
- $H^{3}\subset\On$：3次斉次多項式全体($0$を含む)
- $T$:$T\R f\cap H^{3}\subset H^{3}$の$\CC$-ベクトル空間としての直交補空間$\longrightarrow$(minimal slice)という
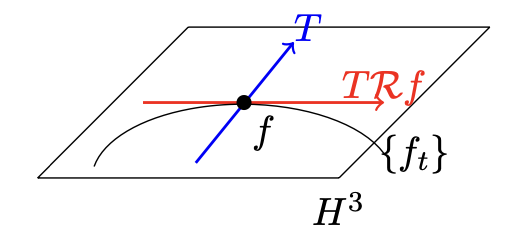minimal slice
$T$の基底$u_{1},\dots,u_{r}$と$a_{1},\dots,a_{r}\in\CC$を用いて$F=f+a_{1}u_{1}+\cdots+a_{r}u_{r}$は$\R$-同値を保たないような変形です. この意義はあとでじっくり話します
$f\in H^{3}$について，射影超平面$V(f)$を
$V(f)=\{[x,y,z]\in\mathbb{P}^{2}| f(x,y,z)=0\}$と定める．この$\R$-分類を与えようと思います.
また曲線同士の関係も知りたいですね
$H^{3}$内で$\R$-同値を考えるので，必然的に微分同相写像$h$は$h(x,y,z)=ax+by+cz$と表せる
とはいえ地道に計算するのは大変なので$f$に$T$の基底$u_{1},\dots,u_{r}$を足すことで変形を試みます
$G\times M\rightarrow M$：群作用
$x,y\in M$に対して軌道$G\cdot x,G\cdot y$を取る
$G\cdot x$が$G\cdot y$を特殊化する$\defa\ \overline{G\cdot x}\supset G\cdot y$
このとき$x\rightarrow y$または$G\cdot x\rightarrow G\cdot y$と書く
特殊化はある"図形"の極限が別の"図形"になると捉えられます.
カスプ$f(x,y,z)=zy^{2}-x^{3}$の接空間$T\R f=\igen{x^{3},y^{3},x^{2}y,xy^{2},y^{2}z,yz^{2},x^{2}z,xyz}_{\CC}$なので$T=\igen{z^{3},xz^{2}}_{\CC}$です．
$F(x,y,z):=f+az^{3}+bxz^{2}=zy^{2}-x^{3}+az^{3}+bxz^{2}$とします
このとき，$z\neq0$を仮定しても良いので$z=1$を代入して$\tF$を得る；$\tF=y^{2}-x^{3}+bx+a$
これはまさに楕円曲線(Weierstrassの標準形)，すなわち非特異
非特異曲線$\tF=0$の極限$a,b\to0$としてカスプ$f=0$が得られる！！
上手く座標変換をしてあげると，結節点の極限としてカスプが得られることもわかりますね〜〜
| 型 | 標準形 | 次元 | |
|---|---|---|---|
| $f_{1}$ | 非特異 | $x^{3}+y^{3}+z^{3}+3txyz$ ($t\in\CC$かつ$t^{3}\neq-1$) | 9 |
| $f_{2}$ | 結節 | $x^{3}+y^{3}-xyz$ | 9 |
| $f_{3}$ | カスプ | $zy^{2}-x^{3}$ | 8 |
| $f_{4}$ | 円と弦 | $x^{3}+xyz$ | 8 |
| $f_{5}$ | 円と接線 | $xy^{2}+yz^{2}$ | 7 |
| $f_{6}$ | 三角 | $xyz$ | 7 |
| $f_{7}$ | 3直線 | $x^{3}+y^{3}$ | 6 |
| $f_{8}$ | 2重線と1直線 | $x^{2}y$ | 5 |
| $f_{9}$ | 3重線 | $x^{3}$ | 3 |
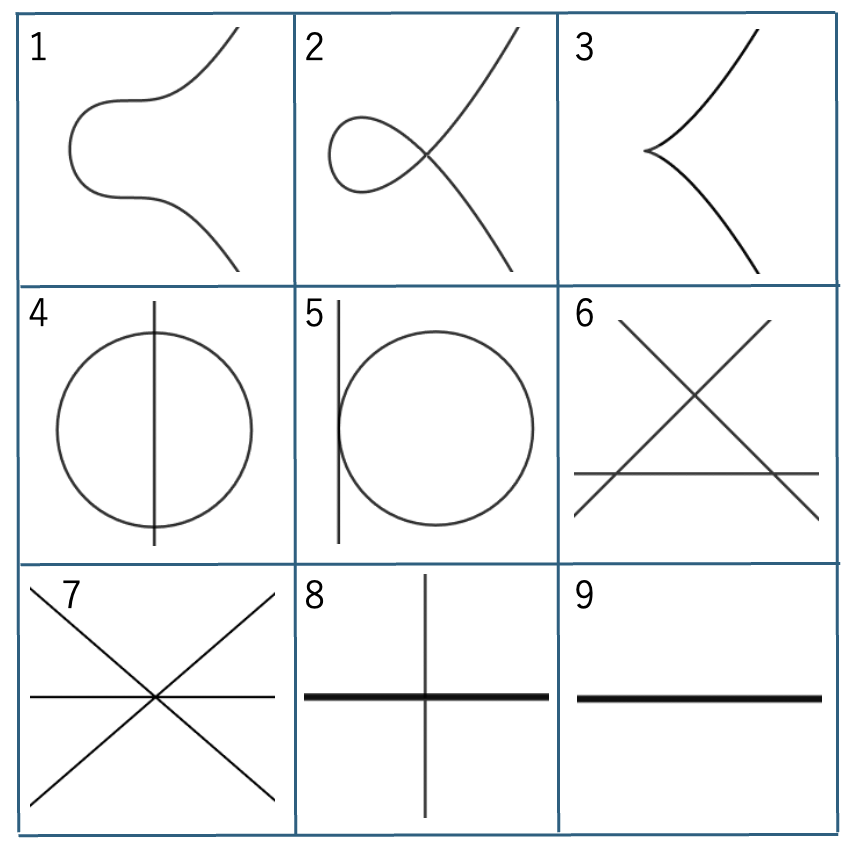曲線の形
- 図2の番号$i$は曲線$f_{i}$に対応
- 次元というのは接空間$T\R f_{i}$を$\CC$-ベクトル空間とみた時の次元$\dim T\R f_{i}$
$\dim T\R f_{i}$が大きければ大きいほど$\dim T_{i}$は小さくなるので, 変形の幅が小さくなると思えます. 下の図3を見ていただければ分かるのですが, 「円と接線」の変形『非特異, 結節, カスプ, 「円と弦」』の極限(特殊化)です. 「円と接線」の接空間の次元$\dim T\R f_{5}=7$であり, カスプの次元$\dim T\R f_{3}=8$より小さいので変形の次元$\dim T_{5}>\dim T_{3}$です. 確かにカスプは『非特異, 結節』の極限であるので, 変形の幅は「円と弦」の方が大きいですね！
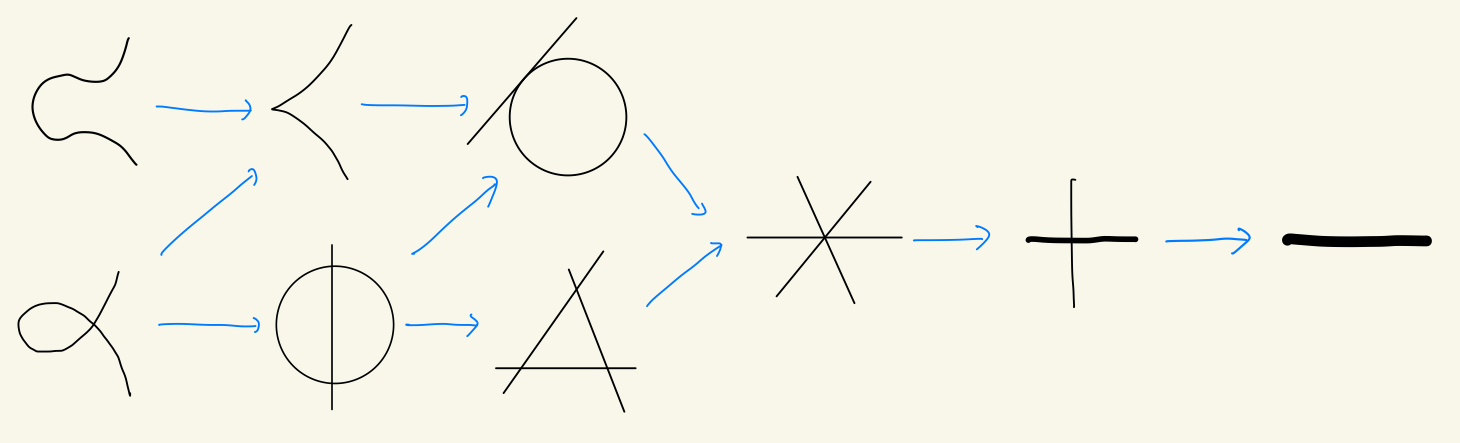曲線の移り変わり
ちなみに今は射影空間で考えています！！つまり無限遠点が備わっています！！つ〜ま〜り〜〜？？そうです！！放物線の両端は無限遠点で繋がって円になるし、カスプは無限遠点を通過して曲がってるわけです！！
(めちゃめちゃ雑な説明ですが, 通常は平面にグラフを書いてるところを, 球面にグラフを書いてるイメージです)
はいどうぞ、特殊化の詳しい説明です(詳しい、とは？)
奇跡の画力
さすがにこの説明は酷い気がしているので、以下の「ここから」から動画見てください
・結節から「円と弦」への特殊化
ここから
・円と弦から3直線
ここから
・カスプから「円と接線」
ここから
ざっくりにはなりますが, 特殊化を証明しましょう！だいぶ選りすぐって「カスプ$\rightarrow$円と接線」を証明します
※読まなくてもいいよ
円と接線$f=x^2y+y^2z$とおく. ヤコビイデアル$J_{f}=\igen{2xy,x^2+2yz,y^2}_{\On}$であるので,
$T\R f=\igen{x^2y,x^3+2xyz,xy^2,xy^2,x^2y+2y^2z,y^3,xyz,x^2z+2yz^2,y^2z}_{\On}$整理して,
$T\R f=\igen{x^2y,xy^2,xyz,x^3,y^2z,x^2z+2yz^2,y^3}_{\On}$より,$T=\igen{z^3,yz^2,xz^2}_{\CC}$
$f$の変形$F=f+az^3+byz^2+cxz^2$を考える.
($a,b,c$を適切に取れば)$F$:カスプであることを示せば$F \overset{a,b,c\rightarrow0}{\longrightarrow}f$が言える
ここで$z\neq0$($\because z=0$を仮定すると,$F=0, \frac{\partial F}{\partial w}=0$の式($w=x,y,z$)から$x=y=0$になるので射影空間の定義に反する)なので$x=\frac{x}{z},y=\frac{y}{z}$と変換して良い(射影空間なので変換できる)
得られた$\tF=x^2y+y^2+a+by+cx$について
$\begin{eqnarray}
\left\{
\begin{array}{l}
\tF=x^2y+y^2+a+by+cx＝０ \\
\tF_{x}=2xy+c=0 \\
\tF_{y}=x^2+2y+b=0
\end{array}
\right.
\end{eqnarray}$ $\cdots(\star)$
の連立方程式の解を
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=x_{0} \\
y=y_{0}
\end{array}
\right.
\end{eqnarray}$
とおくと, $(x_{0},y_{0})$が$\tF$の特異点なので, 原点へ並行移動する. 即ち
$X=x-x_{0}, Y=y-y_{0}$と座標変換して, $(\star)$の式を用いると$\tF=y_{0}X^2+2x_{0}XY+Y^2+X^2Y$が得られ, $y_{0}=x_{0}^{2}$ $(x_{0}\neq0)$とすれば, この特異点はカスプになる.
$\tF_{X}=\tF_{Y}=0$から$x_{0}=\sqrt{-\frac{b}{3}},$ $y_{0}=-\frac{b}{3},$ $c=-\frac{2b}{3}\sqrt{-\frac{b}{3}},$ $a=\frac{b^2}{3}$とすると, $b\rightarrow0$ならば$a,b,c\rightarrow0$によって, $F\rightarrow f$が示される.
$T$の基底として$\{z^3,x^2z,xz^2\}$を取ってきても, 同様のことが言えるのでチェックしてみてください！！
詳細は省略するのですが, 特殊化しない証明には$j$-不変量を用いるものがあります！詳しくは参考文献を調べてみてください.
まとめ
この話は代数曲線, 代数曲面の分類のキーが詰まっていると思います！特にminimal sliceは変形の空間を考えるという点で「うお〜特異点論やってるな！」って感じがします.
実はもう少し分類を進める(単純特異点まで)と, minimal sliceよりも少し一般のcomplete transversalという概念を使い始めます.
次回は未定です！part5も鋭意作成中です
これからもどうぞご贔屓にお願いします🙇
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
