JJMO2025を解いてみた

　解いてみました．問10から自信ないです．それ以前も含めて，間違っていたら指摘してもらえれば訂正します（たぶん）．
　あと，著作権の関係で怒られたりしたら記事は削除します．

問１

　$\gcd(m,n)=\gcd(m,m+n)=\gcd(m,2025)$
　$n>0$より$m<2025$であり，$\gcd(m,2025)<2025$．
　よって$\gcd(m,2025) \leq \dfrac{2025}{3}=675$であり，$m=675, n=675×2$のとき，実際に満たす．

問２

　下図のように$a \sim g$を定める．

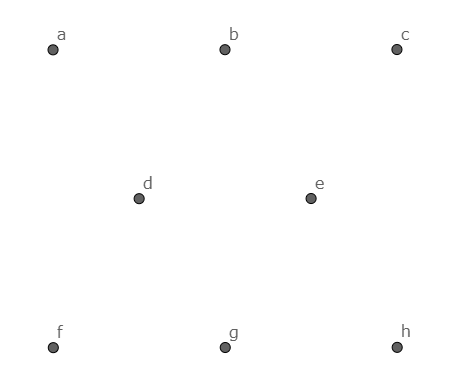
　和が$10$であることから，$a,b$が決まると$c=10-a-b$が確定する．
　同様に考えて$a,b,d$の$3$つが決まると
$$c=10-a-b, f=10-b-d, g=10-a-d, e=2a+b+d-10$$
と順次確定する．ここで$b+e=f+g$を用いて式を作ると，$a+b+d=10$を得る．
　そこで改めて，$d=10-a-b$と置き直そう．今度は
$$c=10-a-b, f=a, g=b, e=a, h=10-a-b$$
と全ての値が確定する．
　つまり$a+b+d=10$を満たすように$a,b,d$を設定すれば，残りの値は順次確定していくということである．
　そのような場合の数は，${}_9 \mathrm{C}_2=36$通りである．

問３

　$\triangle ACD \sim \triangle BED$より，$BE=\dfrac{15}{4}$を得る．
　次に$\triangle ABE \sim \triangle ADF$より，$AD=\dfrac{24}{7}$を得る．
　最後に方べきの定理$DA \cdot DE=DC \cdot DB$を用いて，$BD=\dfrac{18}{7}$．

問４

　正六角形の中心が置かれうる点は$13$点である．下図のように名前を付ける．

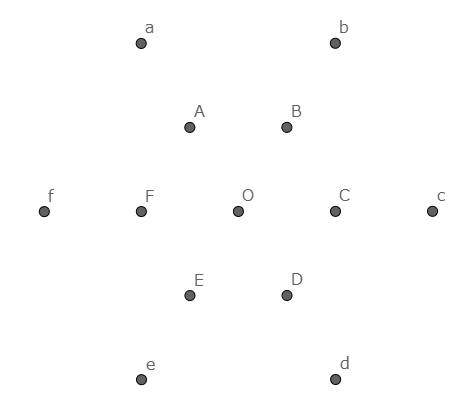
　$13$点から$6$点を選べばよい．ただし正六角形を重ならないように置くという条件は，上図において隣接する$2$点を選べないと言い換えられる．
(i)点$O$を選ぶ場合…$A,B,C,D,E,F$は選べない．$a,b,c,d,e,f$のうち$1$点を選ばなければよいので$6$通り．
　以下の場合分け(ii)~(v)は，点$O$を選ばないものとする．
　ここで隣接する$2$点を選べないことを思い出そう．$A,a$のいずれか，$B,b$のいずれか，$\cdots$，$F,f$のいずれかを$1$つずつ選んでいけばよいことがわかる．
(ii)$A,B,C,D,E,F$から$0$点を選ぶ場合…$1$通り．
(iii)$A,B,C,D,E,F$から$1$点を選ぶ場合…$6$通り．
(iv)$A,B,C,D,E,F$から$2$点を選ぶ場合…$9$通り（正六角形$ABCDEF$の対角線の本数になる）．
(v)$A,B,C,D,E,F$から$3$点を選ぶ場合…$2$通り．
　以上を足し合わせて，$24$通りである．

問５

　こういう問題は実験してみよう．見やすさのため，$N=50^{25}$とおく．何度か操作を行ってみると，次のように変化していくことがわかる．
操作$1$回目：$N-1,1$
操作$2$回目：$N-2,2$
操作$3$回目：$N-3,2,1$
操作$4$回目：$N-4,3,1$
操作$5$回目：$N-5,3,2$
操作$6$回目：$N-6,3,2,1$
操作$7$回目：$N-7,4,2,1$
操作$8$回目：$N-8,4,3,1$
操作$9$回目：$N-9,4,3,2$
操作$10$回目：$N-10,4,3,2,1$
　$1,3,6,10$回目が特徴的であり，次の仮説ができる：

　証明は後回しにする．この予想が正しいと仮定して，先に問題を解いてしまおう．
　$\dfrac{k(k+1)}{2} \fallingdotseq 50^{25}$であるような$k$を求めたい．
　$\dfrac{k(k+1)}{2} \fallingdotseq \dfrac{k^2}{2}$より$k^2 \fallingdotseq 2×50^{25}=2^{26}×5^{50}$
　よって$k \fallingdotseq 2^{13}×5^{25}$．改めて$k = 2^{13}×5^{25}$と置こう．
　$\dfrac{k^2}{2} = 50^{25}$だから，$\dfrac{(k-1)k}{2} < 50^{25} < \dfrac{k(k+1)}{2}$である．
　先ほどの仮説によれば，操作$50^{25}$回目で，石の入った箱は$k$個となるが，最初$50^{25}$個入っていた箱が空箱になることに注意して，答えは$k-1=2^{13}×5^{25}-1$個である．

　なお，仮説の証明については，以下の遷移をもとに帰納的に考えればよい．

• 石の数が$M, n, n-1, \cdots ,1 \rightarrow M-1, n+1, n-1, n-2, \cdots , 1$
• 石の数が$M, n, n-1, \cdots, n-k+1, n-k-1, \cdots, 1 \rightarrow M-1, n,n-1, \cdots, n-k , n-k-2, \cdots,1$

問６

　$2b=a+c$より$c=2b-a$．これを用いてもう一方の式を変形すると
$$b^2-b(c^2+c-1)+c(c+1)(c-1)=0$$
となる．因数分解して$\{b-c(c+1)\}\{b-(c-1)\}=0$に気付けたらあとは簡単である．
(i)$b=c-1$のとき．$a=c-2$であり，$(a,b,c)=(c-2,c-1,c)$が条件を満たすような$c$は$79998$通り．
(ii)$b=c(c+1)$のとき．$a=2c^2+c$であり，$(a,b,c)=(2c^2+2,c(c+1),c)$が条件を満たすような$c$は$199$通り（$2c^2 \fallingdotseq 80000$を解けばよい）．
　足し合わせて，$80197$通り．

問７

$$\triangle FPB:\triangle FPD=\triangle BFC : \triangle DFC =BC:CD$$
$$\triangle EAB:\triangle EAD=\triangle CAB : \triangle CAD =BC:CD$$

ここで，四角形$AEPF$の面積は，$11$であることがわかる．$\triangle BFP$の面積を$S$とおき，$BC:CD=1:k$とおくと，
$S:7=1:k$
$(S+11):13=1:k$
である．よって$k=\dfrac{6}{11}$であり，$\dfrac{BD}{DC}=\dfrac{5}{6}$である．

問８

　条件１：どのように$k$枚のカードを選んでも，選んだカードに書き込まれた整数の平均値は整数となる．
を考えよう（ただし$k < n$とする）．この条件は，次の条件と同値である．
　条件２：全てのカードを$k$で割った余りは等しい
（証明）条件１⇒条件２：任意の$2$枚のカードの置き換えが可能なため．
　　　　条件２⇒条件１：確かめよ．

　従って，問題文の条件「どのように$1$枚以上$n-4$枚以下のカードを選んでも，選んだカードに書き込まれた整数の平均値は整数となる」は，全てのカードを$lcm(1, 2,3, \cdots n-4)$で割った余りが等しい，と言い換えられる．
　この条件を満たすときに，さらに，全てのカードを$n-3, n-2, n-1,n$で割った余りも等しければよい．つまり，$n-3, n-2, n-1,n$が$lcm(1, 2,3, \cdots n-4)$の約数であればよい．
　$n-3,n-2,n-1,n$のいずれもが素数でも素べきでもなければよい．

　素数を小さい順に書いていくと，次のようになる．
$2,3,5,7,11,13,17,19,23,29,31,37,\cdots$
$(n-3,n-2,n-1,n)=(24,25,26,27),(25,26,27,28),(32,33,34,35)$は素数こそ含んでいないが素べき$25,32$を含んでいて不適．答えは$(n-3,n-2,n-1,n)=(33,34,35,36)$．すなわち$n=36$である．

問９(想定解ではない)

　$AC$と$BF$の交点を$P$，$BF$と円$ABCD$の交点を$Q( \ne B)$と置く．
　比較的見つけやすい三角形の相似として

• $\triangle ABC \sim \triangle FDE$（$DF:DE=7:6$と，内接四角形の角度の性質）
• $\triangle BCE \sim \triangle DQE$（円周角の定理）
• $\triangle BCP \sim \triangle DEQ \sim \triangle BEC,\triangle BAP \sim \triangle DFQ $（先の二つから得られる）
• $\triangle ABF \sim \triangle DQF \sim \triangle BPA$（内接四角形の性質）

　とりあえずここまでで，$BP=4, EP=5, AP=\dfrac{44}{7}, BF=\dfrac{49}{4}$などがわかる．
　ここでもう一押しほしいところである．例えば$\triangle ABD \sim \triangle PCE$でどうだろうか．

（このあと，よい解き方がわからない．)
　Stewartの定理から$CP$を求め，$CE,AD,DF,DE$の順に求めれば$CD=\dfrac{63}{8}$となることはわかったが，この方針だと
$$CP=\dfrac{-29+\sqrt{63561}}{56}$$
となるので，想定解ではないはず……．

問１０

　条件より，黒いマスの塗り分け方は大きく分けて$3$通りである．

• 左上隅から右下隅までの対角線を全て黒く塗る．
• 二つの正方形で表せる図aの型
• 三つの正方形で表せる図bの型
  図a
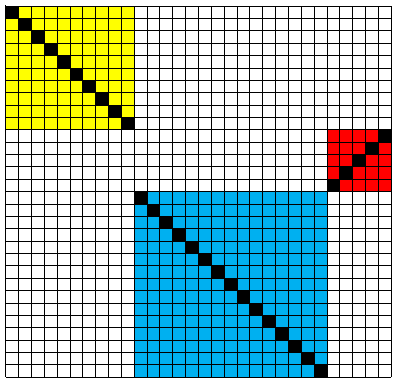  図b
  　図aの黒いマスの塗り方は，水色の正方形の辺の長さが$2 \sim 29$なので$28$通り．
  　図bの黒いマスの塗り方は，
  (i)赤色の正方形が$1$マスの場合…水色の正方形の辺の長さが$2 \sim 28$ なので$27$通り．
  (ii)水色の正方形が$1$マスの場合…$27$通り．
  (iii)赤色も水色も$2$マス以上の場合
  　黄色のマスは$1$マス以上なので，正方形の作り方が${}_{27} \mathrm{C}_2$通り．
  　それぞれに対して，赤色・水色の正方形の黒いマスの塗り方が$3$通り．
  　従って，${}_{27} \mathrm{C}_2×3=1053$通り．

以上を足し合わせて，$1+28+27×2+1053=1136$通り．

問１１（途中）

　まず，問題文の$2$個目の条件を満たすような$a_1, \cdots, a_7$ を作ってみよう．
　$a_1=1, a_2=2, a_3=3$とする．次に$a_4=4$とすると，$a_1+a_4=a_2+a_3$で条件に合致しないので，
$a_4=5$としよう．同様にして$a_5=8$で成立する．
　いきおい$a_6=13$としたくなるが，それでは$3+5+8=1+2+13$で条件に合致しない．よって$a_6=14$としよう．
　最後に$a_7=25$である．
（なお，以上の思考において，例えば$a_1+a_2+a_7>a_4+a_5+a_6$ならば$a_1+a_2+a_3+a_7>a_3+a_4+a_5+a_6$を満たすので，正解した問題数が$3$つまでの場合について考えれば十分である）
　以上で，とりあえず$(a_1,a_2,a_3,a_4,a_5,a_6,a_7)=(1,2,3,5,8,14,25)$を得る．

　このままでは問題文の$1$個目の条件を満たさないので，
$(a_1,a_2,a_3,a_4,a_5,a_6,a_7)=(x+1,x+2,x+3,x+5,x+8,x+14,x+25)$
を考えよう．条件より，

• $x+25<(x+1)+(x+2)$
• $(x+14)+(x+25)<(x+1)+(x+2)+(x+3)$
• $(x+8)+(x+14)+(x+25)<(x+1)+(x+2)+(x+3)+(x+5)$

である．これらを解いて，$x>36$を得る．よって，$(a_1,\cdots, a_7)=(38,39,40,42,45,51,62)$は条件を満たす．

　次に，$a_7 <62$となるような例が存在するか，考えなければならない．
　が……？気分的にはなさそうだが非存在のまともな証明は，私には難しそうなのでお手上げ．