薄い圏の考察(2)．薄い圏の部分圏
薄い圏C(A,{f${_i}$${_j}$}${_i}$${ _\in }$${_A}$,${_j}$${ _\in }$${_A}$}に対して Aの部分類Bによる圏C(B,{f${_i}$${_j}$}${_i}$${ _\in }$${_B}$,${_j}$${ _\in }$${_B}$)は自然に定まります。
そこでさらに{f${_i}$${_j}$}${_i}$${ _\in }$${_B}$,${_j}$${ _\in }$${_B}$の部分類Lを取ります。 ただしLには条件があって、
ⅰ． Lは空類、またはBのすべての元 i に対してf${_i}$${_i}$${ \in }$L.
ⅱ．f${_i}$${_j}$${ \in }$L かつ f${_j}$${_k}$${ \in }$L ならば f${_j}$${_k}$${ \circ }$f${_i}$${_j}$=f${_i}$${_k}$${ \in }$L となる。
をともにみたすとします。
このときLは演算${ \circ }$をもつ射の類とみなせるので、圏が導入できます。この圏C${_A}$の部分圏をC${_A}$(B,L)やC(B,L)などで表します。C${_A}$(B,L)も薄い圏です。
薄い圏C${_A}$に対して、その部分圏をすべてあつめたものを${\mathfrak{C}}$${_A}$とかきます。C${_1}$${ \in }$${\mathfrak{C}}$${_A}$、C${_2}$${ \in }$${\mathfrak{C}}$${_A}$に対してC${_1}$がC${_2}$の部分圏であることをC${_1}$${ \subset }$ C${_2}$で表します。
この圏の包含関係${ \subset }$は例5で見た条件1-3を持ちます。つまり薄い圏C(${\mathfrak{C}}$${_A}$,${ \subset }$)が定義できます。この圏での始対象はC(空圏,空集合)、終対象はC(A,{f${_i}$${_j}$}${_i}$${ _\in }$${_A}$,${_j}$${ _\in }$${_A}$)となります。
以下では、具体例としてAが基数２の集合の場合を見ておきます。すなわち A${ \simeq }${1,2}であり、hom(C${_A}$)${ \simeq }${f${_1}$${_1}$,f${_1}$${_2}$,f${_2}$${_1}$,f${_2}$${_2}$}です。
簡単のため、A={1,2},hom(C${_A}$)={f${_1}$${_1}$,f${_1}$${_2}$,f${_2}$${_1}$,f${_2}$${_2}$}とします。
①Bが空集合のとき、C(B,L)は空圏となります。
②B={1},L={f${_1}$${_1}$}のとき。 演算${ \circ }$によって、定まる関係式は自明な f${_1}$${_1}$${ \circ }$f${_1}$${_1}$ =f${_1}$${_1}$ です。
③B={2},L={f${_2}$${_2}$}のとき。 同様に、定まる関係式は自明な f${_2}$${_2}$${ \circ }$f${_2}$${_2}$ =f${_2}$${_2}$ です。
④B={1,2},L={f${_1}$${_1}$,f${_2}$${_2}$}のとき。 関係式は②と③にあらわれたものです。
⑤B={1,2},L={f${_1}$${_1}$,f${_2}$${_2}$,f${_1}$${_2}$}のとき。 関係式は④にあらわれたものとf${_1}$${_2}$${ \circ }$f${_1}$${_1}$ =f${_1}$${_2}$、f${_2}$${_2}$${ \circ }$f${_1}$${_2}$ =f${_2}$${_2}$です。
⑥B={1,2},L={f${_1}$${_1}$,f${_2}$${_2}$,f${_2}$${_1}$}のとき。 関係式は④とf${_2}$${_1}$${ \circ }$f${_2}$${_2}$ =f${_2}$${_1}$、f${_1}$${_1}$${ \circ }$f${_2}$${_1}$ =f${_2}$${_1}$です。
⑦B={1,2},L={f${_1}$${_1}$,f${_2}$${_2}$,f${_1}$${_2}$,f${_2}$${_1}$}のとき。既述以外の関係式としてf${_2}$${_1}$${ \circ }$f${_1}$${_2}$ =f${_1}$${_1}$,f${_1}$${_2}$${ \circ }$f${_2}$${_1}$ =f${_2}$${_2}$ があります。
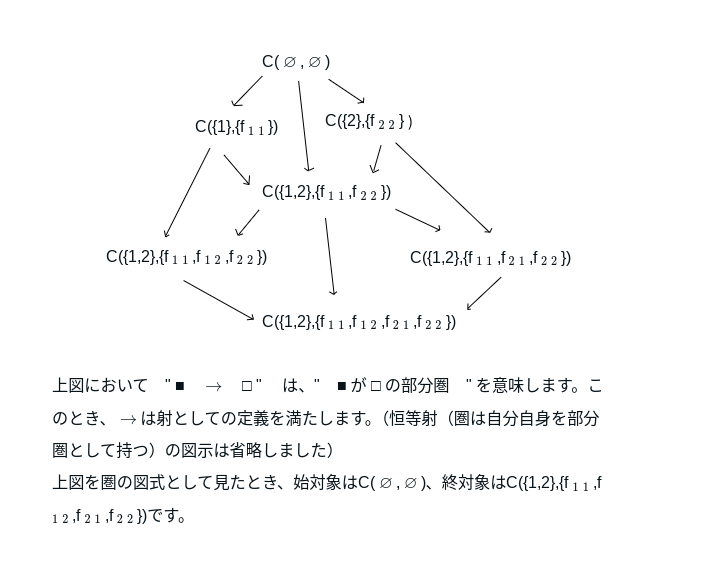①から⑦の関係
