第10回和田杯、僕の解答
ねたばれありまーす。
1
$a$を実数とする.正の整数に対して定義され実数値をとる関数$f$であって,
- 任意の正の整数$x$に対して$|f(x)|<1$
- $\displaystyle \prod_{k=1}^{\infty}f(k)=a$
をみたすものが存在するような$a$をすべて求めよ.
$\left| \displaystyle \prod_{k=1}^{\infty}f(k)\right| <|f(1)|<1$より$|a|<1$.
$f(1)=\frac{|a|}{a}\sqrt{a}$,$f(x)=\sqrt[1/2^x]{a}$とすれば構成できるので答えは$|a|<1$.
構成,結構いっぱいできるはずで,最初に思いついたのは
$f(x)=\frac{(x+k)(x+k+2)}{(x+k+1)^2}$として$f(1)$だけずらすものです.
漸化式的に値を定義していた方もいました.
2
正実数に対して定義され正実数値をとる関数$f$であって,任意の正実数$x,y$に対して
$\left (\ f^{[f(x)]}(y)\ \right )^{[f(x)]}=\left (\ [f(x)]+y\ \right )^{[x+1]}$
が成り立つようなものをすべて求めよ.
ただし正整数$k$に対して$f^k$とは$f^1(x)=f(x),f^{n+1}(x)=f(f^n(x))$で定義されたものであり,実数$r$に対して$[r]$で$r$以下の整数のうち最大のものを表すとする.
$[f(x)]=0$とすると$1=y^{[x+1]}$となり矛盾.よって$[f(x)]$は正整数.
任意の正整数$n$について$n^{1/n}\leq 3^{1/3}<2$なので任意の正整数$n$について$n^{1/n}< t<2$をみたす正実数$t$がとれるのでとる.
$n< t^n$より$y=t^{[f(x)]}-[f(x)]$とでき,すると
$f^{[f(x)]}(y)=t^{[x+1]}$となるので$[x+1]=1$となるようにすれば$f(a)=t<2$なる正実数$a$をとれることがわかる.
$x=a$とすると$f(y)=(y+1)^{[a+1]}\cdots \fbox{A}$
$\fbox{A}$の式に$y=a$を代入して$2>(a+1)^{[a+1]}\geq [a+1]^{[a+1]}$から$[a+1]=1$.これを$\fbox{A}$に当てはめると$f(y)=y+1$.
この式は十分性をみたす.
僕の原案:$f^{[f(x)]}(y)=y+[f(x)]$
を魔改造してもらってできた問題です.
$f$の肩にも,式の肩にも,両肩に荷を載せました.
3
$xy$平面上においてある点が良い点であるとは,その点の$x$座標と$y$座標が共に$1$以上$n$以下の正整数であることを指すものとする.$N$匹のウサギが$(1,1)$から$(n,n)$まで,良い点から良い点への移動のみで移動する.また,ウサギは今いる良い点より$x$座標と$y$座標の少なくとも一方が小さい点には移動できないものとする.このとき,任意の$1\leq i\leq j\leq n$,$1\leq k\leq l\leq n$,$(i,k)\neq (j,l)$をみたす整数$i,j,k,l$に対して,$(i,k)$から$(j,l)$へ移動したウサギが存在したという.ウサギの匹数としてありえる最小値を求めよ.
僕は解けてない
4
$n$を正の整数,$a$を整数としたとき,
$\displaystyle \sum_{d|n}a^d\phi \left (\frac{n}{d}\right )\equiv \sum_{d|n}a^d\mu \left (\frac{n}{d}\right )\ \ (\mathrm{mod}\ n)$
が成立することを示せ.
僕は解けてない
5
鋭角三角形$ABC$の垂心を$H$とする.$H$で$A,B,C$を対称移動させた点をそれぞれ$A',B',C'$とする.$AH$と$BC$の交点,$BH$と$CA$の交点,$CH$と$AB$の交点をそれぞれ$D,E,F$とする.点$X,Y,Z$をそれぞれ三角形$B'EF$,三角形$C'FD$,三角形$A'DE$の外心とする.このとき,
(1)三直線$AX,BY,CZ$が全てある共通の一点を通ることを示せ.
(2)(1)の点を$P$とするとき,$PO:PH$を求めよ.
訂正:(2)について,$O$は三角形$ABC$の外心.
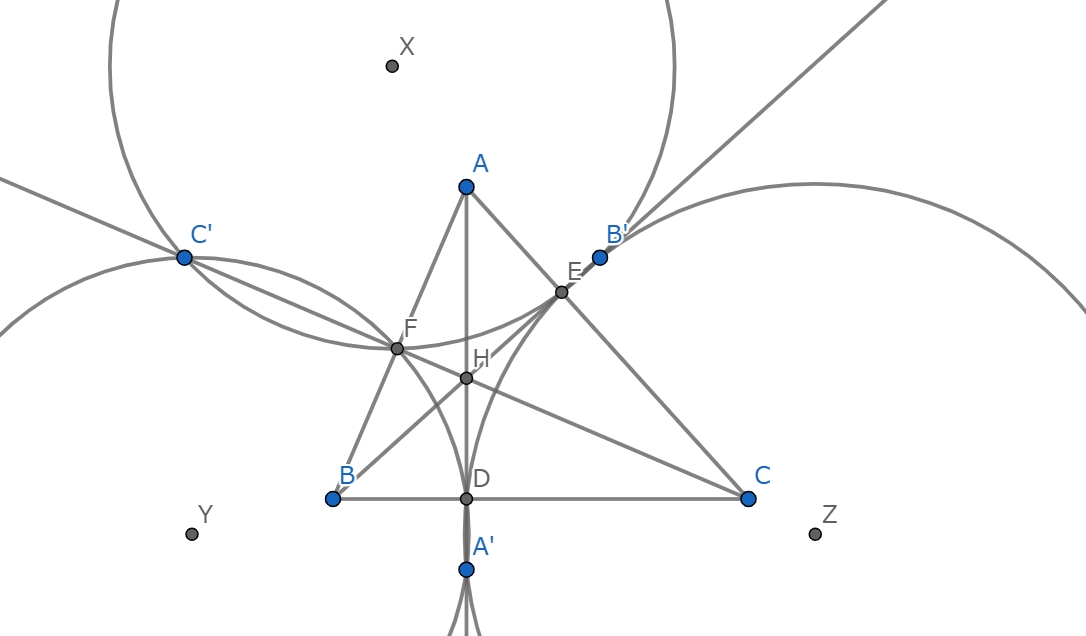
$\angle BFC=\angle BEC=90\degree$だから$B,C,E,F$は共円.
$HC'\cdot HF=HC\cdot HF=HE\cdot HB=HE\cdot HB'$より$B',C',E,F$は共円.
同様に$C',A',D,F$や$A',B',E,D$もそれぞれ共円だから,三角形$XYZ$は三つの線分$A'D,B'E,C'F$の垂直二等分線から成る三角形.
そのため$BC$と$YZ$はいずれも$AD$に垂直なので,$BC//YZ$.
同様に$XY//AB,XZ//AC$より三角形$ABC,XYZ$は相似拡大の関係にあるため(1)が示された.
ここで,辺$BC$の中点を$M$,三角形$ABC$の九点円の中心を$O'$とする.
$X,O'$は定義から線分$EF$の垂直二等分線上にあり,$ME=MB=MF$より$M$についてもそうである.$MO'//AO$より直線$XO'$は三角形$XYZ$の外心を通り,同様に直線$YO',ZO'$についてもいえるので,$O'$は三角形$XYZ$の外心.
$AB:XY=1:x$とする.
$|\triangle YHZ|=\frac{1}{2}YZ(\frac{HD+HA'}{2})=\frac{1}{2}xBC\frac{AD}{2}=\frac{x}{2}|\triangle ABC|$である.同じことを繰り返して足せば
$|\triangle XYZ|=\frac{3x}{2}|\triangle ABC|$である.ここで二つの三角形の相似比は$1:x$だから面積比が$1:x^2$になるので,$x=\frac{3}{2}$.
よって$P$は線分$O'O$を$3:2$に外分する点であるため,$PO:PH=1:2$
![!FORMULA[124][1149640][0]が!FORMULA[125][1150663][0]の中点であることは演習とします.](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FYT31Itp7wUuEnjv9uo47.jpeg?alt=media) $O'$が$OH$の中点であることは演習とします.
$O'$が$OH$の中点であることは演習とします.
他にも同じ式から$H$が三角形$XYZ$の重心だと示していく方針も
6
正実数に対して定義され正実数値をとる関数$f$であって,任意の正実数$x$に対して
$f(x)^2(2f(2f(x))+1)=2f(x)+1$
が成り立つようなものをすべて求めよ.
$f(2f(x))>0$より,$f(x)<3$.
$\displaystyle f(2f(x))=\frac{1}{2f(x)^2}+\frac{1}{f(x)}-\frac{1}{2}$
$\displaystyle f(2f(x))-1=\left ( \frac{1}{2f(x)^2}-\frac{1}{2}\right )+\left (\frac{1}{f(x)}-1\right )=(1-f(x))\left (\frac{3f(x)+1}{2f(x)^2}\right )\cdots \fbox{B}$
ここで,$f(x)\neq 1$と仮定する.
$a_1=f(x),a_{n+1}=f(2a_n)$で定義される数列を考えると,$\fbox{B}$から$\frac{a_{n+1}-1}{a_n-1}=-\frac{3a_n+1}{2a_n^2}<0$であるため,$a_1,a_2,\cdots$は$1$より大きい数と$1$より小さい数が交互に並ぶ数列である.
$\frac{3x+1}{2x^2}>2(x<1),\frac{3x+1}{2x^2}>\frac{5}{9}(1< x<3)$より,$|a_{n+2}|>\frac{10}{9}|a_n|$.
よって十分大きい$n$について$|a_n|>2024$であり,これは$0< f(x)<3$に矛盾する.
したがって$f(x)=1$.これは十分性をみたす.
7
$n$を$3$以上の整数とする.平面上の$n$個の点からなる集合$S$が以下の条件を満たす.
任意の相異なる二点$A,B\in S$に対してある$S$の要素$C$が存在し,三角形$ABC$が正三角形となる.
このとき$n$としてありえる値をすべて求めよ.
$n=3$のときは$S=\{A,B,C\}$を正三角形の頂点からなる集合とすれば条件をみたす.
以下$n\geq 4$とする.
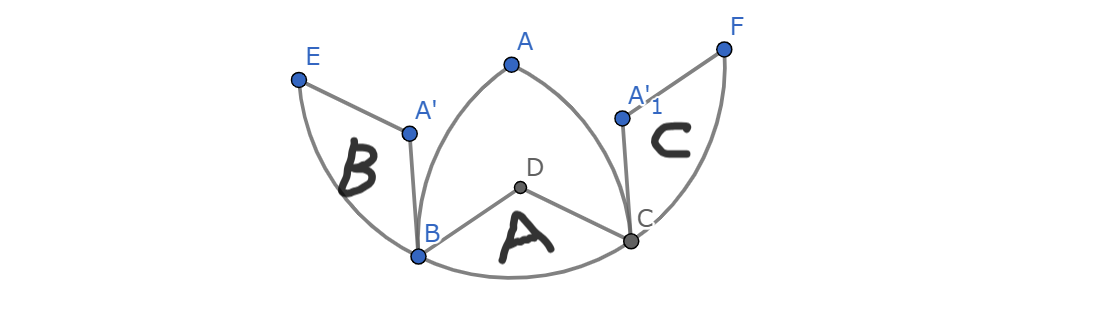
$S$の二つの要素であって,二点間の距離が最大であるような二点$A,B$をとり,三角形$ABC$が正三角形となる点$C$をとる.最大性から$A,B,C$以外の$S$の要素$P$について$AP,BP,CP\leq AB$より,$P$は正三角形$ABC$を含むルーローの三角形内にある.
対称性より$BP,CP\leq AP$とすると$P$の範囲は上図の A である.すると三角形$APQ$が正三角形になるような点$Q$の範囲は上図の B,C であるため,これはルーローの三角形外であるから矛盾する.
したがって$n=3$のみ.
自信作です!
8
$f$を正の整数に対して定義され正の整数値をとる広義単調増加関数とする.(1),(2)それぞれについて条件をみたす$f$をすべて求めよ.
(1)任意の$n\geq k$をみたす正の整数$n,k$について$f(_n\mathrm{C}_k)=\ _{f(n)}\mathrm{C}_{f(k)}$のとき
(2)任意の$n\geq k$をみたす正の整数$n,k$について$f(_n\mathrm{P}_k)=\ _{f(n)}\mathrm{P}_{f(k)}$のとき
二つの問題に特に関連はないので別々に考える.与式への$n,k$の代入をいずれも$P(n,k)$とする.
$P(n,n)$ $f(1)=1$
$P(n+1,n)$ $f(n+1)=\ _{f(n+1)}\mathrm{C}_{f(n)}$より$f(n)=1$または$f(n+1)=f(n)+1$.
- $f(2)=1$のとき
$P(n,2)$ $f(\frac{n(n-1)}{2})=f(n)$より$f(4)=f(6)=f(15)=\cdots$となるため$f(n)=Const.(n\geq 4)$.
$f(_6\mathrm{C}_4)=1$より$Const.=1$で,単調増加性から$f(n)=1$ - $f(2)>1$のとき
単調増加性から$f(n)=1$でないため$f(n+1)=f(n)+1(n\geq 2)$
$f(4)+2=f(6)=f(_4\mathrm{C}_2)=_{f(4)}\mathrm{C}_{f(2)}=_{f(4)}\mathrm{C}_{f(4)-f(2)}=_{f(4)}\mathrm{C}_2=\frac{1}{2}f(4)(f(4)-1)$
$f(4)^2-3f(4)-4=0$より$f(4)=4$
よって$f(n)=n$.
上に行っちゃったからもう一回書くと$f(_n\mathrm{P}_k)=\ _{f(n)}\mathrm{P}_{f(k)}$
$P(n,n)$ $f(n!)=f(n)!$
$P(n,n-1)$ $f(n!)=\ _{f(n)}\mathrm{P}_{f(n-1)}$より$f(n)-f(n-1)=0,1$
- $f(3)>3$
$f(6)=f(3)!$より$f(6)-f(3)=f(3)\{(f(3)-1)!-1\}\geq 4(6-1)$となってしまい矛盾. - $f(3)=3$
$f(6)=6,f(720)=720\cdots$から$f(n)=n(n\geq 3)$
$10=\ _{10}\mathrm{P}_{f(1)}$より,$f(1)=1$
$90=\ _{10}\mathrm{P}_{f(2)}$より,$f(2)=2$
よって$f(n)=n$. - $f(3)<3$
$f(3)!=f(3)$より$f(3)$以降は定数.
あり得るのは次の4つ.
$f(n)=1(n< k)$,$f(n)=2(n\geq k)$ $(k=1,2,3)$
$f(n)=1$
これら全部十分性をみたす(証明略)
9
正の整数に対して定義され正の整数値をとる関数$f$であって,任意の正の整数$a,b,c$に対して
$\displaystyle \frac{f(a)^3+f(b)^3+f(c)^3-3abc}{f(a)+f(b)+f(c)}$
が整数になるようなものをすべて求めよ.
$x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-zx)$より問題の条件は
$\displaystyle \frac{3(f(a)f(b)f(c)-abc)}{f(a)+f(b)+f(c)}$が整数になることと同値.この分数への$a,b,c$の代入を$P(a,b,c)$で表す.
$P(a,a,a)$ $f(a)$は$a^3$を割り切る.よって$f(1)=1$
$P(a,1,1)$ $f(a)+2$は$3(f(a)-a)$を割り切るので$3a+6$を割り切る.よって$5$以上の素数$p$について,$f(p)=1,p$
- $f(p)=p$をみたす素数$p$が無数に存在するとき
$P(a,p,p)$ $f(a)+2p$は$3p^2(f(a)-a)$を割り切る.$p$を十分大きくすれば$f(a)+2p$は$p$と互いに素であるから$f(a)+2p$は$3(f(a)-a)$を割り切る.
$3|f(a)-a|< f(a)+2p$より$f(a)=a$. - ある整数$M$が存在して,素数$p$が$p>M$のとき$f(p)=1$であるとき
$f(n)=1$とする.
$P(a,n,n)$ $f(a)+2$は$3(f(a)-an^2)$を割り切るので$3an^2+6$も割り切り,$f(1)=1$から$3a+6$も割り切るので,$3an^2+6n^2$を割り切るため$6(n^2-1)$を割り切る.
任意の$5$以上の素数または$16,9$である$q$について$p^2-1$が$q$で割り切れない素数は無限に存在するので(証明略)
$f(a)+2$は$6\cdot 8\cdot 3=144$を割り切る.
$f(3)=1,3,9,27$であることから$f(3)=1$であるため$f(a)+2=6(9-1)=48$を割り切る.
ここで,$a$が奇数なら$f(a)$が$a^3$を割り切ることから$f(a)+2$も奇数であるため$48$の奇約数が$1,3$であることと合わせて$f(a)=1$となる.
$P(a,a,n)$ $2f(a)+1$は$3(f(a)^2-a^2n)$を割り切るので$3(4a^2n+1)$を割り切る.ここで$n=2f(a)+1$とすると$2f(a)+1$と$4a^2n+1$は互いに素だから,$2f(a)+1$は$3$を割り切る.よって$f(a)=1$.
10
非負整数の組$(a,b,c)$であって,
$(a^b-c^{ab-a-b})(a^c-b^c)(b^b-c^a)=8abc$
をみたすものをすべて求めよ.
和田杯で唯一解答者が出なかった問題.長いので別の記事に分けて書こうと思う.
略.
$(a,b,c)$は
- $(a,b,0)$ $(a,b)=(0,0)$または$a,b\geq 2$
- $(0,0,c)$
- $(0,1,c)$ $c\neq 0$
- $(5,3,2)$
11
垂心を$H$,外心を$O$,外接円を$\Gamma$とする鋭角三角形$ABC$がある.辺$BC$の中点を$M$とし,辺$BC$の垂直二等分線が直線$AB,AC$と交わる点をそれぞれ$P.Q$とし,線分$PQ$の中点を$N$とする.直線$AH$と$\Gamma$の交点のうち$A$でない方を$D$,直線$D P$と$\Gamma$の交点のうち$D$でないものを$E$,三角形$ENP$の外接円と直線$AB$の交点を$K$とする.二つの直線$OH,KM$が点$R$で交わるとき,$OR:RH$を求めよ.
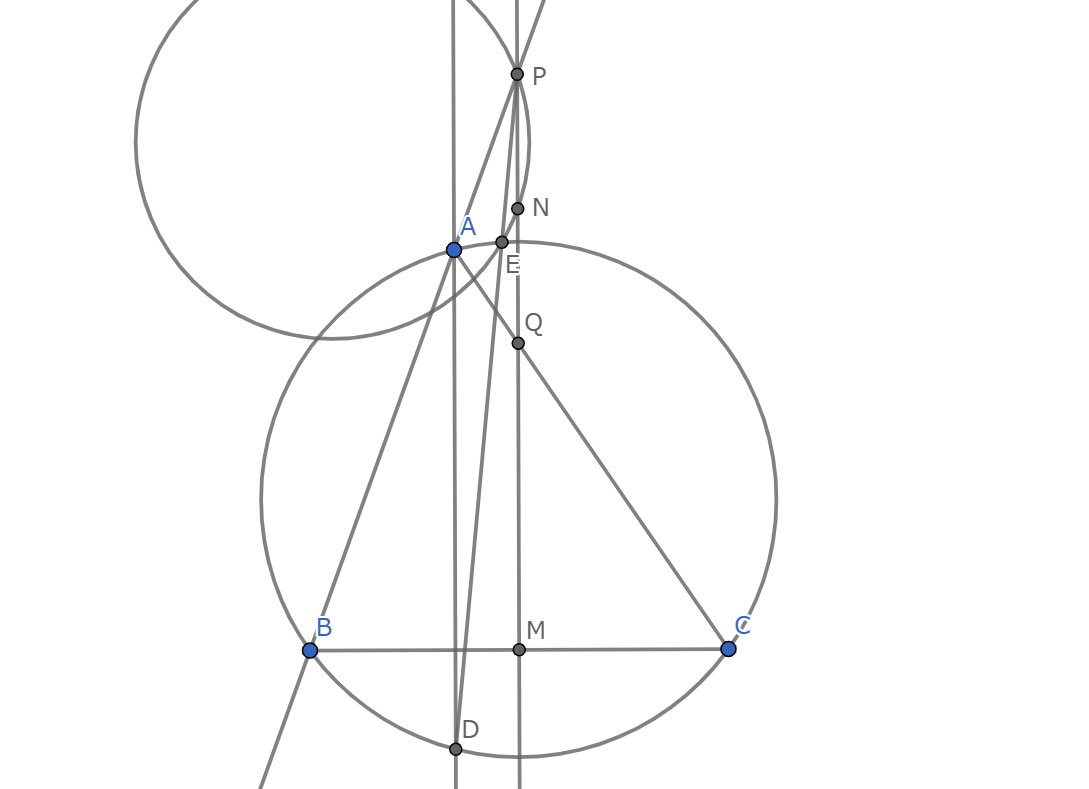
全てを知ってる作問者目線ということでめちゃくちゃ一致法をします
三角形$ABC$の九点円の中心を$R'$,重心を$G$,直線$MR'$と$AB$の交点を$K'$,半直線$MH$と直線$AB$,$\Gamma$の交点を$H',L$とする.
angle-chace(容易だから略)より$B,M,Q,K',L$は共円.$\angle PK'Q=90\degree$
$\angle NPK'=\angle NK'P$
$[H',A;K',P]=[H,G;R',O]$で$\angle ALH'=90\degree$より直線$LA$は角$K'LP$を二等分する.
$\angle ALK'=\angle ALB-\angle BLK'=\cdots =\angle K'PN$($R'M//AO$とかを使う)
よって$L,K',N,P$は共円.
典型構図(NP=NK')より三角形$PAL$の外接円は直線$PQ$に$P$で接する.この円を$\omega_1$とする.
$AD//PQ$より$\angle QPE=\angle EDA=\angle EBP$であるから三角形$EBP$の外接円は直線$PQ$に$P$で接する.この円を$\omega_2$とする.
$\Gamma,\omega_1,\omega_2$の根心は$PQ,AL$の交点$N$であるため$B,E,N$は共線.
$\angle LED=\angle LCD=\angle LMD=\angle LK'D$より$L,K',E,P$は共円.というわけで$K$と$K'$が一致して$R$と$R'$も一致するので答えは$1:1$.
$[H,G;R',O]$を使いたかった問題
12
正の整数の組$(x,y,n)$であって,
$x^{y!}+y^{x!}=2024^n$
をみたすものをすべて求めよ.
対称性から$x\leq y$とします.
$x=1$なら$y=2024^n-1$.
$x\geq 2$なら$x!,y!$はいずれも偶数だから$x^{y!}+y^{x!}$という平方数の和が$11$の倍数になるよということで$11$が$4k+3$型素数であることから$x,y$は$11$の倍数.
すると$\mathrm{mod}\ 31$(ここは$13$でも多分いい)を考えて$n$が$3$の倍数になるので,フェルマーの最終定理よりだめ.
よって解は$(x,y,n)=(1,2024^n-1,n),(2024^n-1,1,n)$
作問者による解はフェル終とかジグモンとか使ってないんですって。
13
鋭角不等辺三角形$ABC$において,内心を$I$,内接円を$\omega$とする.辺$BC,CA,AB$と$\omega$の交点をそれぞれ$D,E,F$とする.三角形$AEF$の外接円と三角形$ABC$の外接円の交点のうち$A$でないものを$A_1$,$I$を直線$BC$で対称移動させた点を$A_2$とし,三角形$DA_1A_2$の外接円を$\omega_A$とする.同様に$\omega_B,\omega_C$を定める.
(1)$\omega_A,\omega_B,\omega_C$はある共通の二点を通ることを示せ.
(2)三角形$ABC$の外心を$O$とする.(1)の二点が直線$OI$上にあることを示せ.
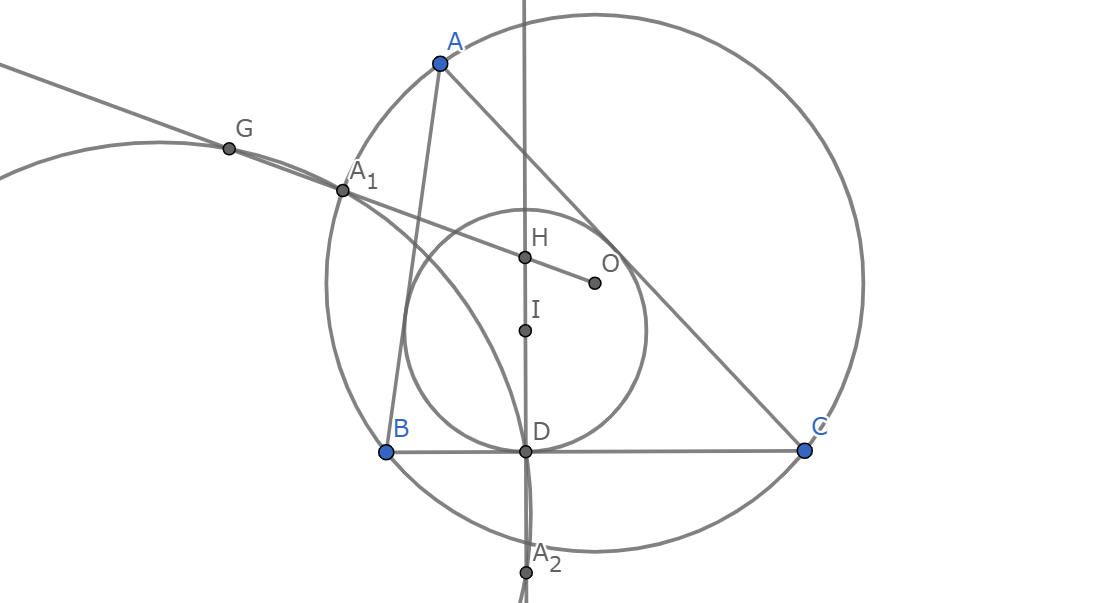
上図みたいな$G,H$と$A$を含まない弧$BC$の中点$M$をとる.
有名事実として$A_1,D,M$は共線(証明は読者への課題).
$OM//HD,OA_1=OM$より,$HA_1=HD$であるため$GA_1=DA_2=ID$
したがって三角形$ABC$の内接円の半径を$r$,外接円の半径を$R$とすると
$\mathrm{Pow}_{\omega_A}(I)=ID\cdot IA_2=2r^2$ $\mathrm{Pow}_{\omega_A}(O)=OA_1\cdot OG=R(R+r)$
これは$A,B,C$によらない値なので,直線$OI$は三円$\omega_A,\omega_B,\omega_C$の根軸.
$A_1D,B_1E,C_1F$の共点とかを使うのかと思ったらそのままいけてしまった.そっちの共点を使うルートもあるらしい.
14
鋭角三角形$ABC$において,$A$から辺$BC$に下ろした垂線の足を$D$,$D$から辺$AB,AC$に下ろした垂線の足をそれぞれ$E,F$とする.三角形$ABC$の外接円と直線$EF$との交点二つを$P,Q$とする.三角形$ABC$の外接円と直線$AD$の交点のうち$A$でない方を$X$とし,辺$BC$上に$BD=CY$をみたす点$Y$をとる.線分$XY$の中点を$M$としたとき,三角形$PQD$の外接円と三角形$BMC$の外接円は互いに接することを示せ.
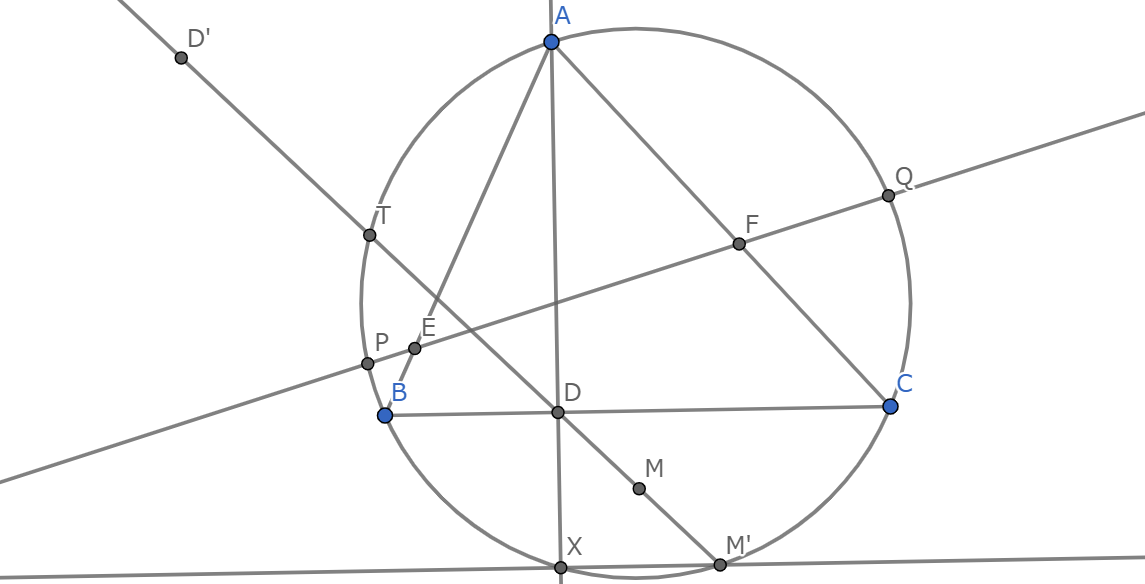
上図みたいな$T,M',D'$をとる.
中心$A$半径$AD$の円での反転で$P,Q$は不動だから$AP=AQ=AD=AD'$
$DD'\cdot DM=DT\cdot DM'=DB\cdot DC$
よって二円は$D'$で交わる.
あとは$BM=CM$に着目すれば有名な話になる.
$D'$さえとれればどうやってもできそう
15
$AB< AC$なる鋭角三角形において,内心を$I$,$I$から$BC$に下ろした垂線の足を$D$とする.直線$BC$上に$AX=XD$なる点$X$をとる.ここで,$X$から直線$AI$に下ろした垂線の足を$P$,辺$BC$の中点を$Q$としたとき,三角形$ABC$の外接円と三角形$XPQ$の根軸を$l$とする.線分$ID$の中点を$Y$としたとき,$l$が$Y$を通ることを示せ.
長さ追跡をします.座標じゃないし余弦定理とかも使わないし許されると思ってる.
$A$から$BC$におろした垂線の長さを$h$,角$A$内の内接円,外接円の半径をそれぞれ$r,R$とする.
$AI\cdot AJ=AB\cdot AC=AG\cdot AM$より$AD:DK=AI:IM=AG:GJ$であるため$BC//KJ$.
$QM=\frac{R-r}{2}$より$KM=\frac{R+r}{2}$.
$h:R=AG:GJ=AI:IM=DI:MK-DI=r:\frac{R-r}{2}$より$h=\frac{R-r}{2Rr}$.
 D',G,J,K,M,N,U,Zをとる.
D',G,J,K,M,N,U,Zをとる.
$BD\cdot DC+rQN=Rr+rQN$(三角形$BDI,JD'B$の相似から)
$=r(R+QN)=\frac{2r}{R+r}\frac{R+r}{2}KN=\frac{h}{h+R}KM\cdot KN=\frac{AD}{KA}KA\cdot KU=AD\cdot KU$
$AD\cdot DK=AD\cdot DU+AD\cdot KU=BD\cdot DC+(BD\cdot DC+rQN)=2(BQ^2-DQ^2)+rQN=2QN\cdot QM-2DQ^2+rQN=2QN(QM+\frac{r}{2})-2DQ^2$
より$\frac{1}{2}AD\cdot DK=QN(QM+\frac{r}{2})-DQ^2$
$QX=DX+DQ=\frac{DK\cdot DZ}{DQ}+DQ=\frac{DK\cdot DA}{2DQ}+DQ=\frac{QN(QM+\frac{r}{2})-DQ^2}{DQ}+DQ=\frac{QN}{DQ}(QM+\frac{r}{2})$であるため
$QX:QN=QM+\frac{r}{2}:DQ=MQ+DY:DQ$,よって$MY$と$NX$は垂直.この交点を$H$とすると,$\angle MHN=90\degree$より$H$は三角形$ABC$の外接円上にあり,$\angle XHM=\angle XPM=\angle XQM=90\degree$より$X,H,P,Q,M$は共円.そのため二円の根軸は直線$MH$であり,これは$Y$を通るので示された.
ここに乗ってないやつは後日別記事で上げようと思います.
