【自由研究】単振り子の周期の厳密解

はじめに

この実験は，「第19回全国物理コンテスト物理チャレンジ2023」の「第1チャレンジ2023実験レポート課題」の実験課題に基づき行われています．

振り子の周期を、振れ角を変えて調べてみよう
単振り子の周期を測定する実験では振れ角を小さくして行います が、振れ角を大きくしていくと周期はどうなるでしょうか。振り子の 振れ角と周期の関係について、実験を行って調べてみましょう。 周期を正確に測る工夫、減衰の小さい振り子の作製、振れ角と周期 の関係についての考察などを期待しています。

物理チャレンジについてはこちらから： 全国物理コンテスト 物理チャレンジ！

概要

参考文献1によるとによると，単振り子の周期は「振れが小さいとき，周期は振幅によらず，糸の長さと重力加速度の大きさだけで決まる．これを振り子の当時性という．」とある．つまり，
単振り子の振幅が微小のとき，周期は，
$$ T=2\pi\sqrt{\frac{l}{g}} $$
のように表されるが，振幅が一般の角のとき，周期は楕円積分を用いると，
$$ T=2\pi \sqrt {l\over g}\Bigl\{ \sum \limits _{n=0}^{\infty }\Big[{(2n-1)!!\over (2n)!!}\Big]^{2}n ^{2n}{\theta _0\over 2}\Bigr\} $$
と表される．ただし，$!!$は二重階乗．これを利用して以下の実験を行った．

実験１

上記の周期の厳密解にどれほどの正確性があるのかを，振幅$\theta_0[{\mathrm{\degree}}]$と弦の長さ$l[{\mathrm{m}}]$を変えて，カメラで単振り子が振れる様子を撮影し，周期を測定することによって調べた．

実験2

振幅$\theta_0[\degree]$を変えて，周期の変化について，カメラで単振り子が振れる様子を撮影し，周期を測定する事によって調べた．
実験2から，周期と振幅の関係について，周期が初期の振幅の六次関数として表されることを発見し，その理由を実験1と理論的考察から推測した．
また，空気抵抗と慣性モーメントについての考察も行い，単振り子の測定した周期と理論的な周期のずれについて徹底的に検証を行った．

実験の目的

今回の実験の目的を以下のように設定した．

実験手法

実験に使用したもの

実験道具（実験自体に使用したもの）

• 単振り子（島津理化機械株式会社製 TN‐3 形，ケニス株式会社製 No.110-0210 単振り
  子 SP ）．金属球：スチールボール1 5/8（直径：2a = 413mm，質量：m = 286g）．弦：
  ピアノ線（太さ：0.35mm）．
  単振り子（金属球を使用した）
  単振り子（弦を使用した）

• 鉄製スタンド

• 分度器

• C型クランプ（鉄製スタンドを机に固定するのに使用）

• 3.5ｍメジャー

• 段ボールとコピー用紙Ａ４で作成した角度確認用分度器
  角度確認用分度器

• ペン

• 卓上ボール盤（段ボールに穴をあけるのに使用）

測定道具（実験の測定及び解析に使用したもの）

• iPhoneXR（撮影用）
• 三脚
• パソコン（ストップウォッチ用と解析用）

実験原理

以下，単振り子の弦の長さを$l[\mathrm{m}]$（この節では，単振り子のおもりを質点として扱うが，実験においては，おもりの半径を加えた長さを弦の長さ$l$とする．），振幅を$\theta[\mathrm{rad}]$（$\theta$は振り子が振れ始めてからの経過時間$t[\mathrm{s}]$の関数），周期を$T[\mathrm{s}]$，小球の質量を$m[\mathrm{kg}]$，重力加速度を$g[\mathrm{m/s^{2}}]$，最下点の位置を$O$，$O$点から円弧に沿った変位を$x[\mathrm{m}]$と表す．
振幅が非常に小さいとき，単振り子の周期は以下のように表される．
\begin{equation} T=2\pi\sqrt{\frac{l}{g}} \tag{1}\label{period_approximation} \end{equation}

なお，周期がこのように表される理由は以下のようである．

円弧の接線方向の運動方程式を解く．
\begin{split} m\frac{d^2x}{dt^2}=-mg\sin\theta & \Longleftrightarrow \frac{d^2x}{dt^2}=-g\sin\theta \end{split}
$x=l\theta$であるので，
\begin{align} l\frac{d^2\theta}{dt^2}=-g\sin\theta\Longleftrightarrow \frac{d^2\theta}{dt^2}=-\frac{g}{l}\sin\theta \tag{2}\label{theta_function} \end{align}
$\theta$が十分に小さいとき，$\sin\theta\simeq\theta$として考えられるので，
\begin{split} \frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta \end{split}
この二階微分方程式を解くと，
\begin{split} \theta(t)=C\sin(\sqrt{\frac{g}{l}} t+\phi) \end{split}
ただし，$C,\phi$は任意定数．そしてこの式は単振動を表すので，角速度$\omega$は，$\omega=\sqrt{\dfrac{g}{l}}$となり，周期$T$は，
\begin{equation} T=\frac{2\pi}{\omega}=\frac{2\pi}{\sqrt{\frac{g}{l}}}=2\pi\sqrt{\frac{l}{g}} \end{equation}
となる．

では，$\theta$を任意の大きさの角として，厳密解を求めるとどうなるのか．以下，簡略化のために$\theta$の時間一階微分を$\dot{\theta}$，時間二階微分を$\ddot{\theta}$と記す．式\eqref{theta_function}の両辺に$\dot{\theta}$をかけて，右辺を左辺に移行する．
\begin{equation} \ddot{\theta}\dot{\theta}+\frac{g}{l}\dot{\theta}\sin\theta=0 \Longleftrightarrow \frac{d}{dt}\biggl[\frac{1}{2}\dot{\theta}^2-\frac{g}{l}\cos\theta\biggl]=0 \end{equation}
よって，$\dfrac{1}{2}\dot{\theta}^2-\dfrac{g}{l}\cos\theta$は定数となるので，定数$E$と置く．（$E$はEnergyの頭文字である．実際，位置エネルギーの基準点を最下点に置くと，振り子の持つ力学的エネルギー（位置エネルギーと運動エネルギーの和）は，$\dfrac{1}{2}ml^2\dot{\theta}^2+mgl(1-\cos\theta)$となり，上の式と対応している．）
$\theta(0)=\theta_0$のとき，$\dot{\theta}=0$だとすると，
\begin{equation} E=-\frac{g}{l}\cos\theta_0 \end{equation}
よって，
\begin{equation} \frac{1}{2}\dot{\theta}^2-\frac{g}{l}(\cos\theta-\cos\theta_0)=0 \Longleftrightarrow \dot{\theta}^2=\frac{2g}{l}(\cos\theta-\cos\theta_0) \end{equation}
いま，$\theta=\theta_0$から$\theta=0$までの運動を考えると，
\begin{equation} \dot{\theta}=-\sqrt{\frac{2g}{l}(\cos\theta-\cos\theta_0)} \end{equation}
さらに，$\theta=\theta_0$から$\theta=0$までの運動にかかる時間は$\dfrac{T}{4}$であるので，
\begin{split} \therefore T&=4\int_0^{\frac{T}{4}} dt \\ &=4\int_{\theta_0}^0\frac{1}{-\sqrt{\frac{2g}{l}(\cos\theta-\cos\theta_0)}}d\theta \quad(\because\dot{\theta}=\frac{d\theta}{dt}\Longleftrightarrow\dot{\theta}dt=d\theta) \\ &=2\sqrt\frac{2l}{g}\int_0^{\theta_0}\frac{1}{\sqrt{\cos\theta-\cos\theta_0}}d\theta \end{split}
ここで，$\sin\dfrac{\theta}{2}=\sin\dfrac{\theta_0}{2}\sin\phi$を満たす$\phi$に変数変換すると，
\begin{equation} T=4\sqrt{\frac{l}{g}}\int_0^{\frac{\pi}{2}}\frac{d\phi}{\sqrt{1-\sin^2\frac{\theta_0}{2}\sin^2\phi}} \end{equation}
となり，第一種完全楕円積分（楕円積分の節を参照）の形となる．よって楕円積分の節で求めた結果を用いて計算すると，
\begin{align} T&=4\sqrt {l\over g}\int _{0}^{\pi \over 2}{1\over \sqrt {1-\sin ^{2}{\theta _0\over 2}\sin ^{2}\phi }}d\phi \\ &=4\sqrt {l\over g}K(\sin{\theta_0\over 2}) \\ &=2\pi \sqrt {l\over g}\Bigl\{ \sum \limits _{n=0}^{\infty }\Big[{(2n-1)!!\over (2n)!!}\Big]^{2}\sin ^{2n}{\theta _0\over 2}\Bigr\} \tag{3}\label{period_exact} \end{align}
となる。ただし，$!!$は二重階乗．

なお、簡略化のため、関数$\sigma(\theta_0)$を以下のように定める．
\begin{equation} \sigma(\theta_0)=\sum \limits _{n=0}^{\infty }\Big[{(2n-1)!!\over (2n)!!}\Big]^{2}\sin ^{2n}{\theta _0\over 2} \end{equation}

Pythonを利用した級数の計算方法

前節から$T$の厳密解\eqref{period_exact}が分かったが，無限級数の形で表されているため，実際に計算しつくすことは不可能である．そのため，できるだけ理論値の正確性を向上させるために，プログラミング言語Pythonを利用して，$T$の数値計算を行う．以下のコードを使用する．ただし定数aは角度であり，常々設定する．
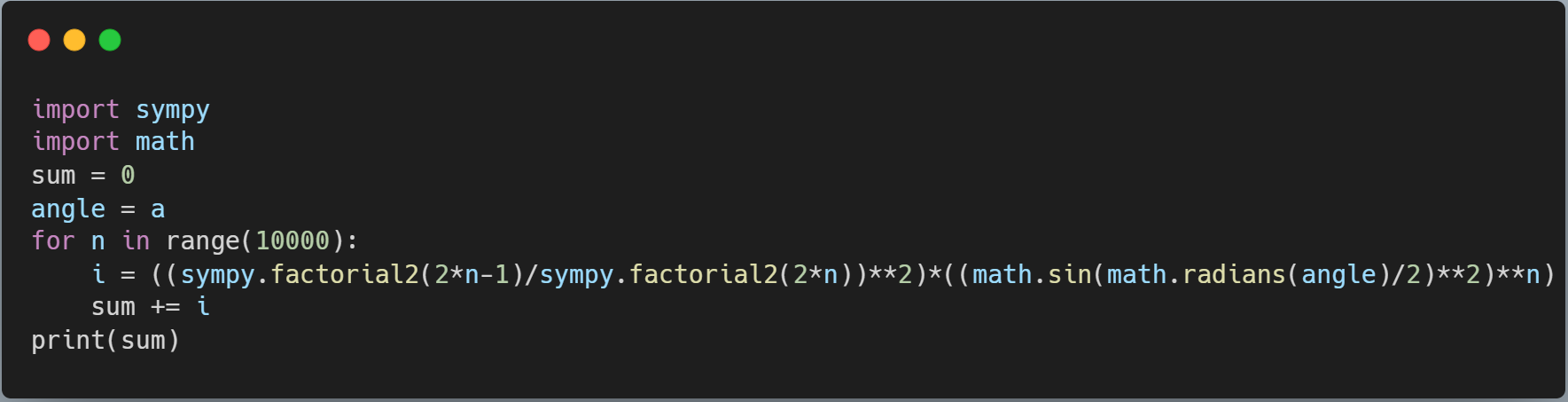使用したソースコード
これによって得られた，$\sigma(\theta_0)$の値は以下の表の通りである
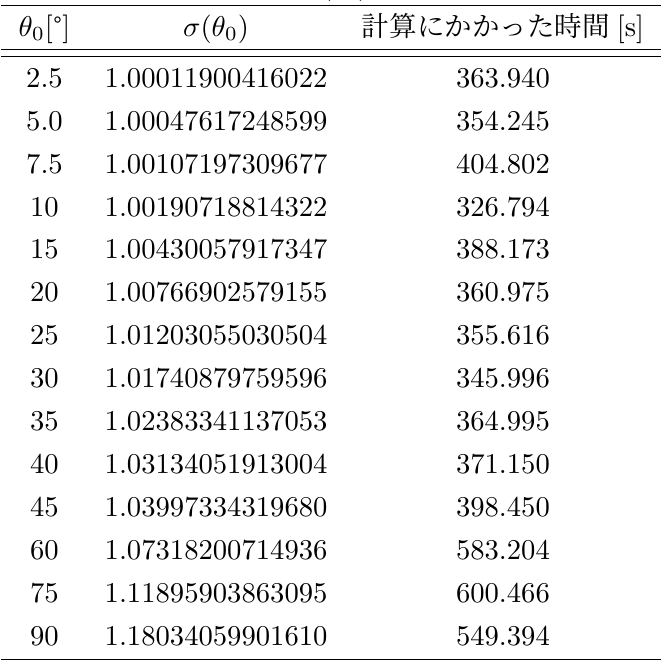得られた値
一個の角度あたり、300～600秒くらいの計算時間がかかった．

実験に使用した値

• 測定場所における重力加速度　$g_s=9.796895\mathrm{m/s^2}$^[1]
• 円周率　$\pi=3.1415926535$

実験手順

大まかな実験手順は以下の通りである．実験ごとの細かい解析手順についてはその下で示す．

1. 弦の長さ（金属球の中心から弦についたリングと支持棒の接点までの長さ）を調べる対象に合わせて測り，固定．
2. 実験装置を図のようにセットする．
3. 鉄製スタンド横に設置したパソコンのストップウォッチをスタートさせておく．
4. 実験者Aが振り子の位置を調節し，実験者BがiPhoneのカメラから振り子の位置を確認し，適切な位置を指示する．
5. 実験者BがiPhoneのスローカメラ^[2]をスタートさせ，実験者Aが振り子をそっと放し，振り子が5回以上振れたときに実験者Bがカメラを止める．
6. 撮影した動画を確認し，振り子が静止した状態で振り子の中心を通るように鉛直方向に引いた線（線$I$とする．）を利用して，初めの時間（振り子が線$I$を初めて通過したときの時間．）と終わりの時間（振り子が5回振れたときに線$I$を通過した時間．）を計測することによって，その差から5回振れる間にかかった時間（$5T$）を測定する．
   実験装置

実験１

実験1では，目的1のため，以下の表のような場合について実験を行う．それぞれの場合について，5回ずつ行う．その後の手順は以下の通りである．
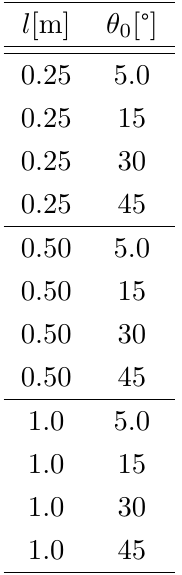実験１の実験対象

1. 式\eqref{period_exact}について，$\sigma(\theta_0)=\sigma$として，変形すると，
   \begin{equation} T=2\pi \sqrt {l\over g}\sigma(\theta_0) \Longleftrightarrow g=\frac{4\pi^2l\sigma^2}{T^2} \tag{4}\label{g_e} \end{equation}
   となる．
2. また，式\eqref{period_approximation}について，変形すると，
   \begin{equation} T=2\pi\sqrt{\frac{l}{g}} \Longleftrightarrow g=\frac{4\pi^2l}{T^2} \tag{5}\label{g_a} \end{equation}
   となる．
3. 測定した周期$T$から，上の式により，重力加速度を算出する．ここでは，式\eqref{g_e}から算出した重力加速度を$g_e$，式\eqref{g_a}から算出した重力加速度を$g_a$と記す．（添え字の$e$はexactの頭文字，$a$はapproximateの頭文字．）
4. 実際の重力加速度$g_s$と算出した重力加速度$g_e$，$g_a$の相対誤差から，厳密解の正確性を考察する．

実験２

実験2では，目的2のため，以下の表のような場合について実験を行う．それぞれの場合について，5回ずつ行う．（なお，実験1で計測済みの値についてはその値を使用した．）その後の手順は以下の通りである．
実験２の実験対象

1. 計測した周期から，縦軸が周期，横軸が初期の振幅のグラフを作成する．
2. 近似曲線をExcelの機能を用いて作成．
3. 振幅と周期の関係について考察する．

誤差を少なくするための実験方法の工夫

$T$の測定誤差について

測定した$T$の値が実際の値とずれていたら，もちろんそれだけの誤差が生じる．よって，測定した$T$の値と実際の値との測定誤差を小さくするために，スローカメラを利用し，できるだけ誤差が生じないようにした．

$l$の測定誤差について

測定した$l$が計算に用いた値とずれていたら，もちろんそれだけの誤差が生じる．よって，$l$による測定誤差を小さくするために，金属球の直径とリングの大きさを差し引いた値でピアノ線の長さを測定した．

円錐振り子による誤差について

単振り子が円錐振り子になってしまえば，もちろんそれだけの誤差が生じる．よって，円錐振り子による誤差を小さくするために，実験者Aが振り子の振れる面からずれないように，真横から手を放した．

減衰による誤差について

単振り子が振れるうちに，減衰し，周期の測定誤差が生じる可能性がある．しかし，実験を進める過程で，5回振れる間ならほとんど無視していいほど減衰も少ないとわかった．（5回振れてすぐ後の$\theta$の最大角を見ると，初期の振幅とほぼ変わらないとわかった．）よって，減衰による誤差を小さくするために，周期を測定する際，単振り子が5回振れるときの時間を測定した．

金属球の回転による誤差

ピアノ線がねじれたままの状態で金属球を放すと，金属球が回転しながら振れて，周期の測定誤差が生じる可能性がある．よって，手を放した状態で金属球の回転が止まったところから，初期の振幅を合わせた．

カメラの固定位置による誤差について

カメラの画面から実験者Bは初期の振幅を合わせるわけだが，カメラの位置により，実際は違う振幅に合わせられる可能性がある．よって，カメラの固定位置による誤差を小さくするために，支持棒の奥行きが見えなくなるように，つまりカメラの画面に支持棒の側面の円の部分しか見えないようにカメラを固定した．

スタンドの棒の揺れによる誤差

鉄製スタンドの棒が単振り子の弦に引っ張られることにより，横に揺れ，単振り子の周期に測定に影響することが想定されたので，鉄製スタンドをC型クランプにより机に固定し，スタンドの棒が揺れないようにした．

実験結果

実験１の結果

以下，実験1の結果を示す．縦軸は実際の重力加速度$g_s$と算出した重力加速度$g_e$，$g_a$の相対誤差，横軸は初期の振幅である．青色でプロットしてある点が、計測した値である．

実験1 $g_e$ 相対誤差（$l$=0.25m）

実験1 $g_a$ 相対誤差（$l$=0.25m）

実験1 $g_e$ 相対誤差（$l$=0.50m）

実験1 $g_a$ 相対誤差（$l$=0.50m）

実験1 $g_e$ 相対誤差（$l$=1.0m）

実験1 $g_a$ 相対誤差（$l$=1.0m）

実験２の結果

以下，実験2の結果を示す．縦軸が周期，横軸が初期の振幅である．青色でプロットしある点が計測した周期，緑色の線が線形近似した直線，オレンジ色の線が6次関数で多項式近似した曲線である．
実験2 振幅と周期の関係（$l=1.0m$）

考察

周期の厳密解の妥当性について

まず，実験1について考察する．実験1から作成したグラフより，厳密解（式\eqref{period_exact}）で算出した重力加速度$g_e$は実際の重力加速度$g_s$との相対誤差がどの弦の長さにおいても$1\%$以内に抑えられている．一方，近似解（式\eqref{period_approximation}）で算出した重力加速度$g_a$は実際の重力加速度$g_s$との相対誤差がどの長さにおいても初期の振幅が大きくなるにつれ大きくなり，$\theta_0=45\degree$においては$8\%$となっている．しかし，近似解も初期の振幅が小さいときには厳密解と同程度の正確性を持っていると言える．

振幅と周期の関係について

次は，実験2について考察する．実験2から作成した図15より，周期$T$は初期の振幅$\theta_0$の6次関数のように表現できることを発見した．ここで，厳密解（式\eqref{period_exact}）の式についてもう一度見てみると，
\begin{align} T&=2\pi \sqrt {l\over g}\Bigl\{ \sum \limits _{n=0}^{\infty }\Big[{(2n-1)!!\over (2n)!!}\Big]^{2}\sin ^{2n}{\theta _0\over 2}\Bigr\} \\ &=2\pi \sqrt {l\over g}\Bigl\{ 1+{1\over 4}\sin ^{2}{\theta_0 \over 2}+{9\over 64}\sin ^{4}{\theta_0 \over 2}+{225\over 2304}\sin ^{6}{\theta_0 \over 2}+\cdots \Bigr\} \end{align}
となり，$\sin{\dfrac{\theta_0}{2}}$の6次関数となっている．では，$\theta_0$と$\sin{\dfrac{\theta_0}{2}}$の関係はどうなっているだろうか．
$\theta$と$\sin{\dfrac{\theta_0}{2}}$の関係
図16は，青色の点で$\theta_0$と$\sin{\dfrac{\theta_0}{2}}$の関係をプロットしてある．また，オレンジ色の直線はプロットした青色の点の線形近似である．すると，$\theta_0$の一次関数的に$\sin{\dfrac{\theta_0}{2}}$が表現できていることがわかる．
実験1から，厳密解（式\ref{period_exact}）がある程度の妥当性を持っていることがわかっているから，つまり，周期が振幅の6次関数のように表現できることが正しいと言える．ということは，無限級数の6次の項までの影響がそれほど大きいということだろうか．実際，以下のPythonのコードを利用して計算してみると，
使用したソースコード
$\sigma(\theta_0)$の6次の項までの値
となる．ただし，表の左から3つ目の「$\sigma(\theta_0)$における$\sigma(\theta_0)$の6次の項までの値の割合$[\%]$」とは，表の左から2つ目の「 $\sigma(\theta_0)$の6次の項までの値」を「$\sigma(\theta_0)$」で割り，100を掛けた値である．

重力加速度の真の値とのずれについて

考察の周期の厳密解の妥当性についての節で，厳密解（式\eqref{period_exact}）で算出した重力加速度は，実際の重力加速度との相対誤差が1$\%$に抑えられていると述べた．しかし，やはり，誤差が生じてしまっている．なぜだろうか．その可能性は主に5つ考えられる．

$T$の測定誤差により誤差が生じた可能性

$T$の測定誤差はかなり大きな影響を与える．実際には，$\Delta T=\pm0.015\mathrm{s}$程度の誤差が生じていた可能性が疑われる（スローカメラで測定した際，一コマ$\pm0.015\mathrm{s}$程度だとわかった．）．改善方法としては，撮影に使用したカメラを高性能なものにして，パソコンの編集機能を利用する方法である．ただ，今回予算的に行うことができなかった．今後の改善点である．

ピアノ線のねじれ及びリングと支持棒の接触部分の干渉により誤差が生じた可能性

今回実験に使用した，ピアノ線はかなり古いものであったので，少しねじれており，実験を行う際は延ばしてから使用したが，残っていた小さなねじれから誤差が生じた可能性がある．また，弦に取り付けたリングは，$\theta_0=40{\degree}$までなら，支持棒に干渉せずにおもりが振れることができる．しかし，$\theta_0=40{\degree}$以上においては，リングが支持棒に干渉してしまう場合があった．これにより，誤差が生じた可能性がある．

実際の重力加速度がずれている可能性

実験場所の重力加速度$g_s$を参考文献GSI，GPSを使用して設定したが，実験場所が地上5階であったので高さを$15{m}$としたが，これが実際とは違い，誤差が生じた可能性がある．この議論については，後で詳しく考察するが，結果的には，ほとんど無視していいほどの誤差であると結論付ける．

空気抵抗により誤差が生じた可能性

厳密解を導く過程で，速度に比例する抵抗力を一切無視して，計算を行った．しかし，実際は空気抵抗により，測定した周期に誤差が生じていた可能性がある．これについては，後で詳しく考察する．

単振り子の慣性モーメントにより誤差が生じた可能性

厳密解を導く過程で，おもりを単なる質点として，計算を行った．しかし，実際は単振り子の慣性モーメントにより，測定した周期に誤差が生じていた可能性がある．これについては，後で詳しく考察する．

国土地理院の重力値測定サービスと単振り子による重力加速度の測定について

参考文献GSI2によると，「国土地理院は、全国で重力測量を実施し、国際的な基準に整合した重力値を提供しています。重力値は、正確な標高を決めるために必要であるほか、地下の活断層や資源の探査、計量機器の較正などに広く利用されています。日本の標高の基準は、測量法で平均海面と定められており、この平均海面を陸域にまで仮想的に延長した面をジオイドといいます。国土地理院では、重力測量や水準測量の結果などから、ジオイド・モデルを作成し、提供しています。ジオイド・モデルは、衛星測位で標高を求めるために使用されています。」とある．地上での測定方法について詳しく調べてみると，「重力の測定は、絶対的な重力値を正確に測定する「絶対重力測定^[3]」と、相対的な重力の差を求める「相対重力測定^[4]」に分けられます。国土地理院では、全国に重力の基準となる3種類の重力点（基準重力点、一等重力点、二等重力点）を設置しており、基準重力点の重力を絶対重力測定で、一等重力点及び二等重力点の重力を基準重力点からの相対重力測定でそれぞれ測定しています。」とある．また，それによって得られる絶対的な重力加速度は，「有効数字9桁」とある．つまり，相対的な重力加速度としては，「有効数字7桁」となる．

一方，今回，実験1で周期の厳密解により測定した重力加速度$g_e$の$g_s$との相対誤差は，弦の長さ$l=0.25\mathrm{cm}$，初期の振幅$\theta_0=5.0{\degree}$においては，$0.20\%$程度に抑えることができた．つまり，算出した重力加速度$g_e$は，有効数字2桁程度までなら信頼できると言える．実際には，重力値は，大気圧や潮汐力などによっても変化するため，国土地理院の測定方法ほどの精度とは言えないが，ある程度の精度を持って，単振り子の周期の測定により重力加速度を算出することができる．

また，国土地理院による重力値測定は，「測定する高さを$1\mathrm{m}$高くすると、重力値の7桁目が3程度減少する。」とあるので，真の値とのずれについての可能性3つ目「実際の重力加速度がずれている可能性」は，ほぼ否定できる．

空気抵抗が与える影響について

空気抵抗が与える影響はどれほどのものなのだろうか．単振り子のおもりに物体の速度に比例する抵抗力がはたらくとする．そのとき，空気抵抗$f_v$は，Stokesの抵抗法則（詳しくは，参考文献Tatsumiを参照．）より，
\begin{equation} f_v=6\pi\eta a v \end{equation}
である．ただし，おもりの半径を$a$，空気の粘性率を$\eta$とする．この空気抵抗による項を単振り子における運動方程式に加えると，
\begin{equation} m\frac{d^2x}{dt^2}=-6\pi\eta a\frac{dx}{dt}-mg\sin\theta \Longleftrightarrow m\frac{d^2x}{dt^2}+6\pi\eta a\frac{dx}{dt}+mg\sin\theta=0 \end{equation}
ここで，$\theta$が十分小さいとすると，$\sin\theta\simeq\dfrac{x}{l}$より，上の式は，
\begin{equation} m\frac{d^2x}{dt^2}+6\pi\eta a\frac{dx}{dt}+mg\frac{x}{l}=0 \Longleftrightarrow \frac{d^2x}{dt^2}+\frac{6\pi\eta a}{m}\frac{dx}{dt}+\frac{g}{l}x=0 \end{equation}
となる．これは，二階の線形常微分方程式となっているので，一般解は，
\begin{equation} x=C_1e^{\lambda_1t}+C_2e^{\lambda_2t} \end{equation}
と書ける．ただし，$C_1,C_2$は定数であり，$\lambda_1,\lambda_2$は特性方程式$\lambda^2+\dfrac{6\pi\eta a}{m}\lambda+\dfrac{g}{l}=0$の解である．$\lambda_1>\lambda_2$のとき，$\lambda_1,\lambda_2$を求めると，
\begin{align} \lambda_1&=-\frac{3\pi\eta a}{m}+\sqrt{(\frac{3\pi\eta a}{m})^2-\frac{g}{l}}\\ \lambda_2&=-\frac{3\pi\eta a}{m}-\sqrt{(\frac{3\pi\eta a}{m})^2-\frac{g}{l}} \end{align}
となり，よって，一般解は，
\begin{align} x=&C_1\exp{\left(-\frac{3\pi\eta a}{m}t\right)}\exp{\left(t\sqrt{\left(\frac{3\pi\eta a}{m}\right)^2-\frac{g}{l}}\right)}\\ &+C_2\exp{\left(-\frac{3\pi\eta a}{m}t\right)}\exp{\left(-t\sqrt{\left(\frac{3\pi\eta a}{m}\right)^2-\frac{g}{l}}\right)} \end{align}
となる．しかも，実験から，単振り子は加減衰ではなく，減衰振動であるので，$\left(\dfrac{3\pi\eta a}{m}\right)^2-\dfrac{g}{l}<0$である．この条件の下，Eulerの公式$e^{i\theta}=\cos\theta+i\sin\theta$より，解は下のように書き換えられる．
\begin{equation} x=C\exp{\left(-\frac{3\pi\eta a}{m}t\right)}\sin{\left(t\sqrt{\frac{g}{l}-\left(\frac{3\pi\eta a}{m}\right)^2}\right)} \end{equation}
ここで，$C$は任意定数．よって，周期は，
\begin{equation} T=2\pi\sqrt{\frac{l}{g}}\left(\sqrt{1-\frac{l}{g}\left(\frac{3\pi\eta a}{m}\right)^2}\right) ^{-1} \tag{6}\label{T_r} \end{equation}
となる．
この式により導き出された空気抵抗を考慮した理論的な周期を$T_r$と記す．（添え字の$r$はresistanceの頭文字．）また，近似解（式\eqref{period_approximation}）の周期を$T_a$と記す．この式を実験を行った状況に適用する．参考文献Tatsumiによると，室温（約20℃），圧力1気圧において，空気の粘性率は$\eta=1.809\mathrm{g/(cm\cdot s)}$である．また，$2a=413\mathrm{mm}$，$m=286\mathrm{g}$である．単位に気を付けて適用する．実際の周期との差について見ると，以下の表のようになる．表から，空気抵抗を考慮せず初期の振幅を微小とした近似解$T_a$と空気抵抗を考慮し初期の振幅を微小とした解$T_r$の差は，周期の測定誤差である$\Delta T=\pm0.015\mathrm{s}$よりも小さい．
また，初期の振幅を一般の角だとして，空気抵抗を考慮した解を導出すれば，より厳密解（式\eqref{period_exact}）に近づくと推測される．
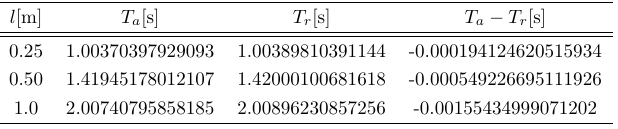空気抵抗を考慮した周期について
つまり，空気抵抗を考慮したところで，それによって生まれる差はほとんど無視していいほどのものであるということである．すなわち，真の値とのずれについての可能性4つ目「空気抵抗により誤差が生じた可能性」は，ほぼ否定できる．

単振り子の慣性モーメントが与える影響について

単振り子の慣性モーメントが周期に与える影響はどれほどのものなのだろうか．おもりの質量を$m$，おもりの半径を$a$とすると，おもり（球）の中心周りの慣性モーメント$I_w$は，
\begin{equation} I_{w}=\frac{2}{5}ma^{2} \end{equation}
となる．（補足を参照）よって，平行軸の定理（補足を参照）により，単振り子の慣性モーメント$I$は，
\begin{equation} I=ml^{2}+\frac{2}{5}ma^{2} \end{equation}
である．ここで，$l$は弦の長さ（支点からおもりの中心までの長さ．）である．振り子が受ける力のモーメント$N$は，振り子が$\theta$だけ振れた位置では，
\begin{equation} N=-mgl\sin\theta \end{equation}
となるので，$\theta$が十分小さいとすると，$\sin\theta\simeq\theta$より，運動方程式は，
\begin{equation} m\left(l^{2}+\frac{2}{5}a^{2}\right)\ddot{\theta}=-mgl\theta \end{equation}
と書ける．これを整理すると，
\begin{equation} \ddot{\theta}=-\frac{g}{l}\cdot\frac{1}{1+\frac{2}{5}\frac{a^{2}}{l^{2}}}\theta \end{equation}
となり，これは単振動の方程式であるから，角振動数を$\omega$とすれば，
\begin{equation} \omega^{2}=\frac{g}{l}\cdot\frac{1}{1+\frac{2}{5}\frac{a^{2}}{l^{2}}} \end{equation}
であるから，周期$T$は，
\begin{equation} T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{l}{g}\left(1+\frac{2}{5}\frac{a^{2}}{l^{2}}\right)} \end{equation}
となる．

この式により導き出された単振り子の慣性モーメントを考慮した理論的な周期を$T_{B}$と記す．^[5]この式を実験を行った状況に適用する．$2a=413\mathrm{mm}$，$m=286\mathrm{g}$である．単位に気を付けて適用する．実際の周期との差について見ると，以下の表のようになる．表から，単振り子の慣性モーメントを考慮せず初期の振幅を微小とした近似解$T_a$と単振り子の慣性モーメントを考慮し初期の振幅を微小とした解$T_B$の差は，周期の測定誤差である$\Delta T=\pm0.015\mathrm{s}$よりも小さい．
また，初期の振幅を一般の角だとして，単振り子の慣性モーメントを考慮した解を導出すれば，より厳密解（式\ref{period_exact}）に近づくと推測される．
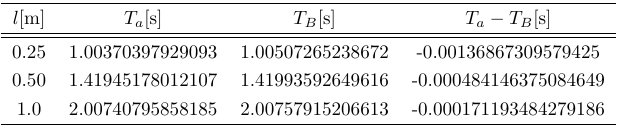単振り子の慣性モーメントを考慮した周期について
つまり，単振り子の慣性モーメントを考慮したところで，それによって生まれる差はほとんど無視していいほどのものであるということである．（しかし，今回の実験とは違って，おもりの半径が弦の長さに比べて，ほぼ同じくらいの大きさとなるとさすがに無視できないほどの差が生まれるはずである．）すなわち，真の値とのずれについての可能性5つ目「単振り子の慣性モーメントにより誤差が生じた可能性」は，ほぼ否定できる．

結論

今回，2つの実験と考察から，以下，4つの事がわかった．

補足

補足では，楕円積分の概要とその応用及び慣性モーメントに関する捕捉事項について述べる．

楕円積分

一般に，$\displaystyle \int_c^xf(x,\sqrt{p(x)})dx(c=\text{const.},p\text{は3次か4次の多項式},f\text{は有理式})$という形の積分のことを楕円積分（Elliptic integral）という．その中でも，第一種完全楕円積分と第二種完全楕円積分と呼ばれるものを導入する．

ここで，$K(m)$について考えると，この積分は解析的に解くことはできない．そのため解析的な積分ではなく，級数展開によってアプローチする．ここで，$\dfrac{1}{\sqrt{1-x}}=\displaystyle\sum _{n=0}^{\infty }\dfrac{(2n-1)!!} {(2n)!!}x^n$を利用すると，
\begin{align} (1-m^2\sin^2\theta)^{-\frac{1}{2}}&=1+{1\over 2}m^2\sin ^{2}\theta +{3\over 8}m^{4}\sin ^{4}\theta +{15\over 48}m^{6}\sin ^{6}\theta +\cdots \\ &=\sum _{n=0}^{\infty }{(2n-1)!!\over (2n)!!}m^{2n}\sin ^{2n}\theta \end{align}
となる．ただし，$!!$は二重階乗．この級数は$m<1$の範囲で一様収束するので，和と積分の順序を入れ替えることが許される．よって，
\begin{align} \displaystyle \int _{0}^{\pi \over 2}\displaystyle (1-m^2\sin ^{2}\theta )^{-{1\over 2}}d\theta &=\int _{0}^{\pi \over 2}\sum _{n=0}^{\infty }{(2n-1)!!\over (2n)!!}m^{2n}\sin ^{2n}\theta d\theta \\ &=\sum _{n=0}^{\infty }{(2n-1)!!\over (2n)!!}m^{2n}\int _{0}^{\pi \over 2}\sin ^{2n}\theta d\theta \\ &={\pi \over 2}\Bigr\{ \sum \limits _{n=0}^{\infty }\Big[{(2n-1)!!\over (2n)!!}\Big]^{2}m^{2n}\Bigr\} \tag{7}\label{wallis_1} \end{align}
\eqref{wallis_1}では，以下のWallisの公式（参考文献wiki2を参照）を利用した．
\begin{equation} \displaystyle \int _{0}^{\pi \over 2}\sin ^{2n}\theta d\theta ={(2n-1)!!\over (2n)!!} \cdot {\pi \over 2} \end{equation}

楕円の周を求める

まず，$x=a\sin\theta,y=b\cos\theta(a>b)$で表される楕円の周の長さを求める．曲線の微小要素の長さ$ds$は，三平方の定理から$ds=\sqrt{dy^2+dx^2}$と表せるので，$dx=a\cos\theta d\theta,dy=-b\sin\theta d\theta$に留意すると，
\begin{align} \displaystyle L &=\intop \limits ds \\ &=\intop \limits \sqrt {dy^{2}+dx^{2}} \\ &=4\int _{0}^{\pi \over 2}\sqrt {b^{2}\sin ^{2}\theta +a^{2}\cos ^{2}\theta }d\theta \\ &=4a\int _{0}^{\pi \over 2}\sqrt {1-\sin ^{2}\theta +{b^{2}\over a^{2}}\sin ^{2}\theta }d\theta \\ &=4a\int _{0}^{\pi \over 2}\sqrt {1-m^2\sin ^{2}\theta }d\theta \ \ \ (0\leq m={\sqrt{a^{2}-b^{2}}\over a}\leq 1) \end{align}
となり，第一種楕円積分の時と同様に級数展開して，
\begin{align} \displaystyle (1-m^2\sin ^{2}\theta )^{1\over 2} &=1-{1\over 2}m^2\sin ^{2}\theta -{1\over 8}m^{4}\sin ^{4}\theta -{3\over 48}m^{6}\sin ^{6}\theta -... \\ &=1-\sum _{n=1}^{\infty }{(2n-1)!!\over (2n)!!}{m^{2n}\over 2n-1}\sin ^{2n}\theta \end{align}
Wallisの公式を適用すると，
\begin{align} \displaystyle L &=4a\int _{0}^{\pi \over 2}\sqrt {1-m^2\sin ^{2}\theta }d\theta \\ &= 4a\int _{0}^{\pi \over 2}\Bigl\{1-\sum _{n=1}^{\infty }{(2n-1)!!\over (2n)!!}{m^{2n} \over 2n-1}\sin ^{2n}\theta d\theta \Bigr\} \\ &= 4a\int _{0}^{\pi \over 2}d\theta-\sum _{n=1}^{\infty }{(2n-1)!!\over (2n)!!}{m^{2n}\over 2n-1}4a\int _{0}^{\pi \over 2}\sin ^{2n}\theta d\theta \\ &= {2a\pi}\Bigl\{ 1-\sum \limits _{n=1}^{\infty }\Big[{(2n-1)!!\over (2n)!!}\Big]^{2}{m^{2n}\over 2n-1}\Bigr\} \end{align}
となる．ただし，$m=\dfrac{\sqrt{a^2-b^2}}{a}$．実際，$a=b=r$とすると，$m=0$となるので，円周の長さ$L=2\pi r$に帰着する．

単振り子の周期の近似解と厳密解の差について

周期の近似解（式\eqref{period_approximation}）と厳密解（式\eqref{period_exact}）の相対差（近似解と厳密解の比から1を引き，100を掛けた．）は，図４のソースコードを利用して求めると以下の表のようになる．
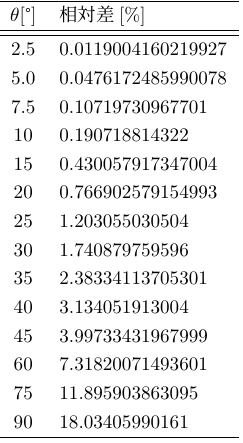近似解と厳密解の相対差
明らかに，角度が大きくになるにつれ厳密解と近似解の差が大きくなるのがわかる．

おもり（球）の中心周りの慣性モーメントについて

まず，半径$a$，高さ$h$の一様な円柱について考える．この円柱について，円柱の軸に関する慣性モーメントを計算する．円柱の軸を$z$軸とする円柱座標系$(r,\theta,z)$をとる．円柱の密度を$\rho$とすれば，$z$軸に関する慣性モーメント$I_z$は，
\begin{equation} I_{z}=\iiint\rho r^{2}dV=\rho\int_{0}^{a}r^{3}dr\int_{0}^{2\pi}d\theta\int_{0}^{h}dz=\frac{\pi}{2}\rho a^{4}h \end{equation}
に等しい．円柱の全質量を$M$とすれば，$M=\pi\rho a^{2}h$であるから，
\begin{equation} I_{z}=\frac{1}{2}Ma^{2} \tag{8}\label{I_z} \end{equation}
となる．
ここで，半径$a$の球体の中心周りの慣性モーメントについて考える．
1つの直径を選んでそれを$z$軸とする．球を$Z$軸に垂直な薄い円盤に分割したとすると，求める慣性モーメントはこれらの円盤の慣性モーメントの総和である．
密度を$\rho$とすれば，$z$の位置にある厚さ$dz$の円盤の質量は$\pi\rho(a^{2}-z^{2})dz$であるから，式\eqref{I_z}により，求める慣性モーメント$I_w$は，
\begin{align} I_{w}&=\int_{-a}^{a}\frac{1}{2}\pi\rho(a^{2}-z^{2})dz\cdot(a^{2}-z^{2})\\ &=\frac{1}{2}\pi\rho\int_{-a}^{a}(a^{2}-z^{2})^{2}dz\\ &=\frac{8}{15}\pi\rho a^{5}=\frac{2}{5}ma^{2} \end{align}
となる．ここでは，球体の全質量$m=\rho\dfrac{4}{3}\pi a^{3}$を使った．

平行軸の定理

単振り子のおもりの慣性モーメントを計算するために以下の定理を導入する．

付録

pdfはこちらから

楕円積分と Python を用いた単振り子の周期の検証とExcel を用いた振幅との関係についての考察