OMC対策（G分野：角度追跡）
本記事の前提知識
外心，内心，垂心と，円周角の定理を知っておけば十分である．
角度追跡とは
競技数学のG分野における，基本中の基本技が角度追跡である．高校数学のカリキュラムの中では「角度追跡」という名称では出現しないし，受験数学でも見かけたことがないので，競技数学に限る技だと言っていいだろう．角度追跡は基本技でありながら，国際数学オリンピックの問題を解く際にもよく用いられる．G分野に取り組むためには，まず身につけなければならない技だと言えよう．
ここまでの前置きをすると，どんなにすごい技かと思われるかもしれない．しかし何ということはない，名前の通り，角度を追いかけていくだけである．
具体例を示そう．
$△ABC$の外心を$O$，垂心を$H$とするとき，$\angle OAC=\angle HAB$を示せ．
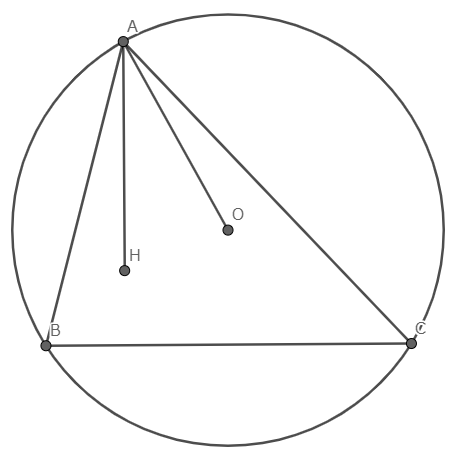
略解
$\angle OAC=\angle HAB=90°-\angle ABC$となる．
$△ABC$の辺$BC$上に点$D$を取ったところ，以下が成立した．
$AB=AC=CD, AD=BD$
このとき$AB:BC$を求めよ．
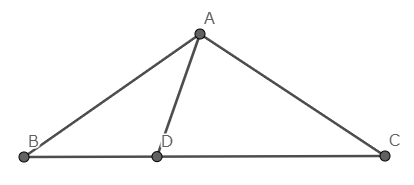
略解
$\angle ABC=\theta$とおいて角度追跡すれば$△ABC \sim △DAB$を得る．よって$BD:AB=AB:BC$である．
$AB=1,BC=x$とおいて二次方程式を解けば，$AB:BC=1:\dfrac{1+\sqrt{5}}{2}$を得る．
重要なのは例題２だろう．角度追跡によって，二等辺三角形や相似に気付いて展望が開けることは，ままあるのだ．
角度追跡の重要性を感じるには，やはりいくつか問題を解いてみるのがいいだろう．
角度追跡から得られる重要な性質
最後に，角度追跡によって得られる重要な性質を二つ紹介しておく．どちらも，競技数学ではよく使われる性質であり，G分野が得意な人は間違いなく覚えているものだ．
角度追跡の練習問題として，実際に証明してみるとよいだろう．
$△ABC$の内心を$I$とし，$AI$と外接円$ABC$の交点を$M(\neq A)$とするとき，$MB=MC=MI$．
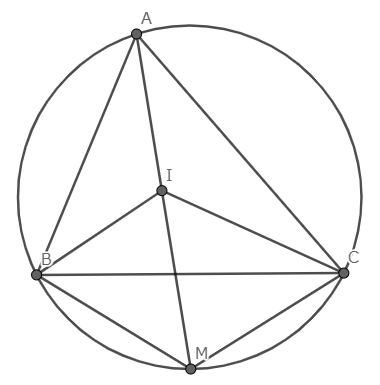
略証
$\angle BIM=\angle BAI+\angle IBA$，$\angle IBM=\angle MBC+\angle IBC=\angle MAC+\angle IBC$より示せる．
$△ABC$の垂心を$H$とする．
- $AH$と$BC$の交点を$D$，$AH$と外接円$ABC$の交点を$X(\neq A)$とするとき$BH=BX,DH=DX$．
- $BC$の中点を$M$とし，$AY$が外接円$ABC$の直径であるとき$MH=MY$．
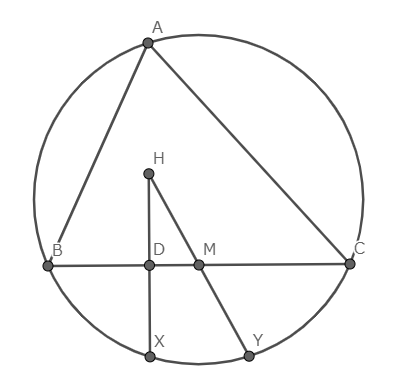
略証
$\angle HBC=\angle DAC=\angle XAC=\angle XBC$より$△BHD \equiv △BXD$．
$\angle HDM=\angle HXY=90°$より$△HDM \sim △HXY$．よって$DH=DX$から$MH=MY$．
この記事を高評価した人
この記事に送られたバッジ
投稿者
