組み合わせとmnCnの形式的冪級数

455

今回示したい式

$\sum_{n = 0}^{\infty} (\binom{m n}{n}) x^{n} = \frac{1}{1 - m x (\sum_{n = 0}^{\infty} \frac{1}{(m - 1) n + 1} (\binom{m n}{n}) x^{n})^{m - 1}}$

まず以下の補題を示します.

$(0, 0)$ から次の図のように対角線 $(m - 1) y = x$ を跨がずに $((m - 1) n, n)$ へと $x, y$ いずれかの正方向に $1$ だけ進み得られる経路の数は $\frac{1}{(m - 1) n + 1} (\binom{m n}{n})$ .
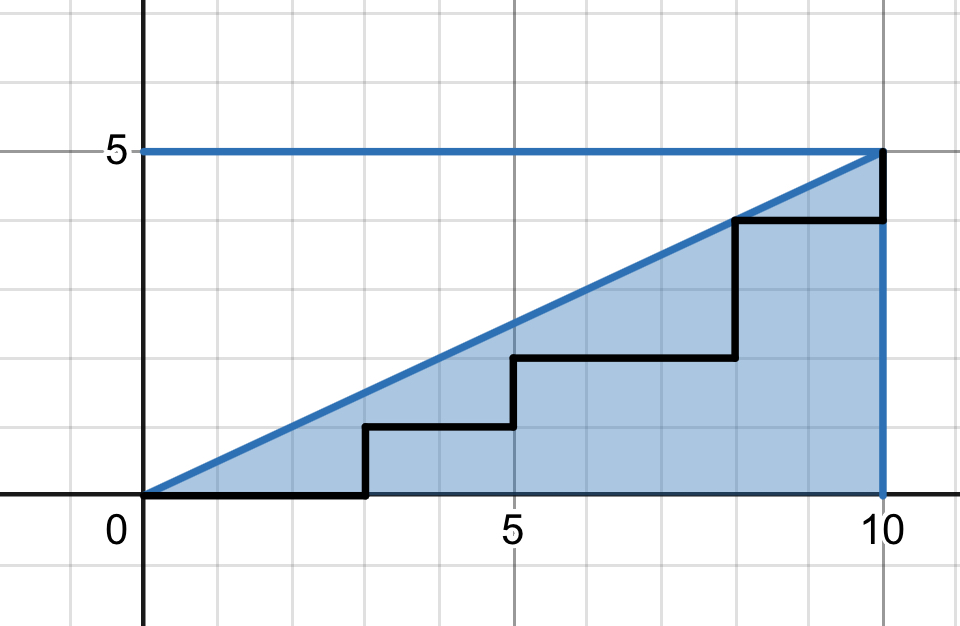m=3,n=5の例

　 $(0, 0)$ から $((m - 1) n, n)$ へと向かう経路のうち対角線を跨ぐ経路の総数を求める.
　今、図のように $(- 1, 1)$ から $((m - 1) n, n)$ へ向かう経路 $ℓ$ を考える.

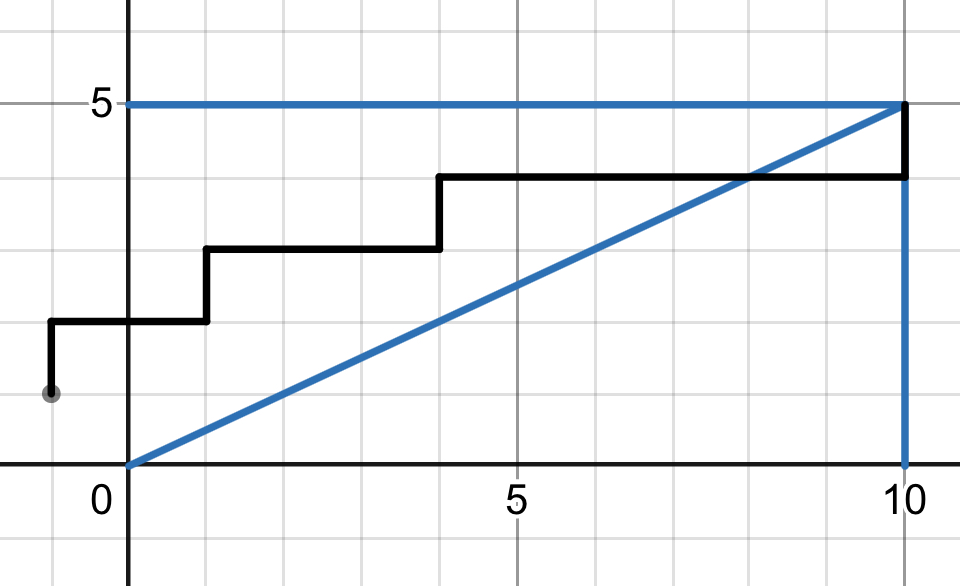
$k = 1, 2, \dots, m - 1$ について $ℓ$ が初めて直線 $(m - 1) y - x = k$ に触れる下図の赤点についてそのひとつ手前までの経路を $180$ 度回転させた経路を図のように赤点のひとつ下に挿入すれば
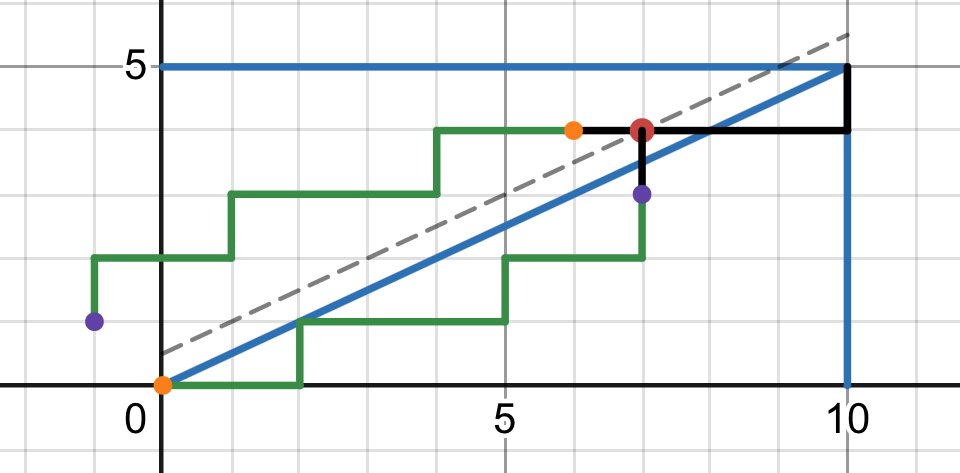k=1 k=1
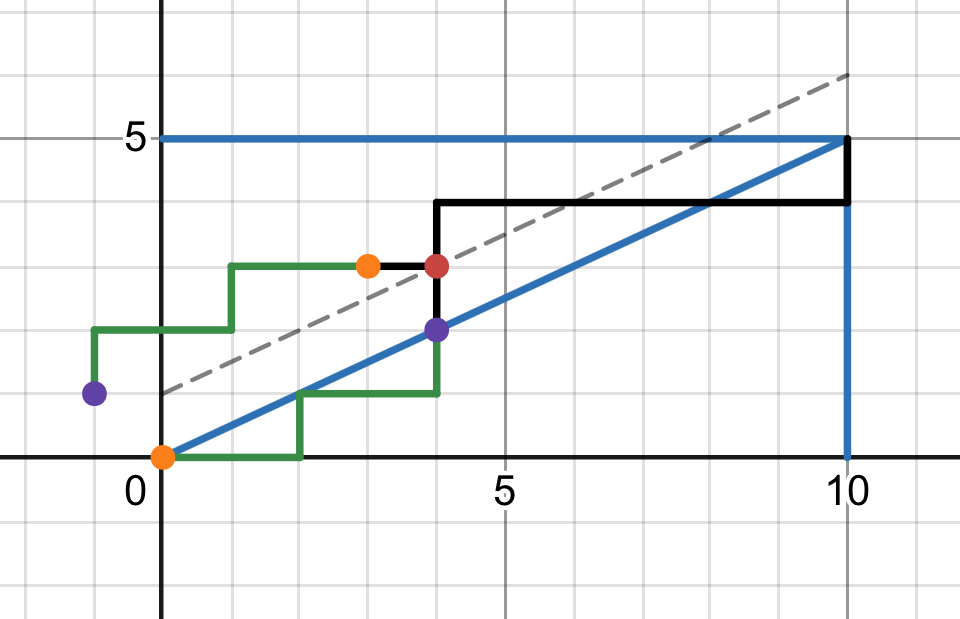k=2 k=2
経路 $ℓ$ から『対角線を跨ぐ経路』に $1$ 対 $m - 1$ の対応を取ることができる. 逆に『対角線を跨ぐ経路』からも一意に対応を取ることができるから, 対角線を跨ぐ経路の総数は $ℓ$ として考えられる経路の $m - 1$ 倍である. したがって, 対角線を跨がない経路の総数は
$(\binom{m n}{n}) - (m - 1) (\binom{m n}{n - 1}) = \frac{1}{(m - 1) n + 1} (\binom{m n}{n}) .$

$(0, 0)$ から直線 $(m - 1) y = x$ 上の点 $((m - 1) n, n)$ へと進み得られる経路の数のうち $((m - 1) n, n)$ 以外の直線 $(m - 1) y = x$ 上の格子点を通らない経路の総数は
$m \times \sum_{n_{1} + n_{2} + \dots + n_{m - 1} = n - 1} \frac{1}{(m - 1) n_{1} + 1} (\binom{m n_{1}}{n_{1}}) \cdot \frac{1}{(m - 1) n_{2} + 1} (\binom{m n_{2}}{n_{2}}) \dots \frac{1}{(m - 1) n_{m - 1} + 1} (\binom{m n_{m - 1}}{n_{m - 1}})$

　以下の画像( $m = 4$ の場合)のように $m$ パターンに分けることができ,画像のように経路を分割(一意性はある)することで,それぞれのパターンで
$\sum_{n_{1} + n_{2} + \dots + n_{m - 1} = n - 1} \frac{1}{(m - 1) n_{1} + 1} (\binom{m n_{1}}{n_{1}}) \cdot \frac{1}{(m - 1) n_{2} + 1} (\binom{m n_{2}}{n_{2}}) \dots \frac{1}{(m - 1) n_{m - 1} + 1} (\binom{m n_{m - 1}}{n_{m - 1}})$
とおりの経路数があることがわかる.
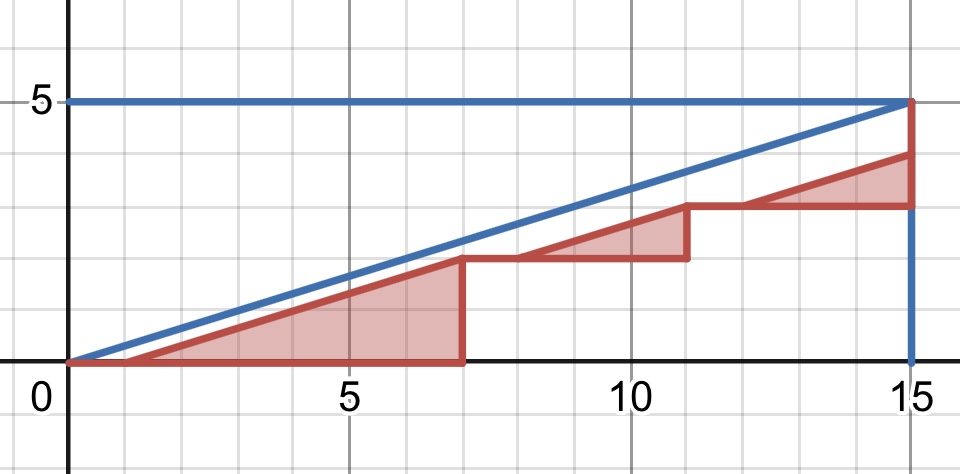パターン1
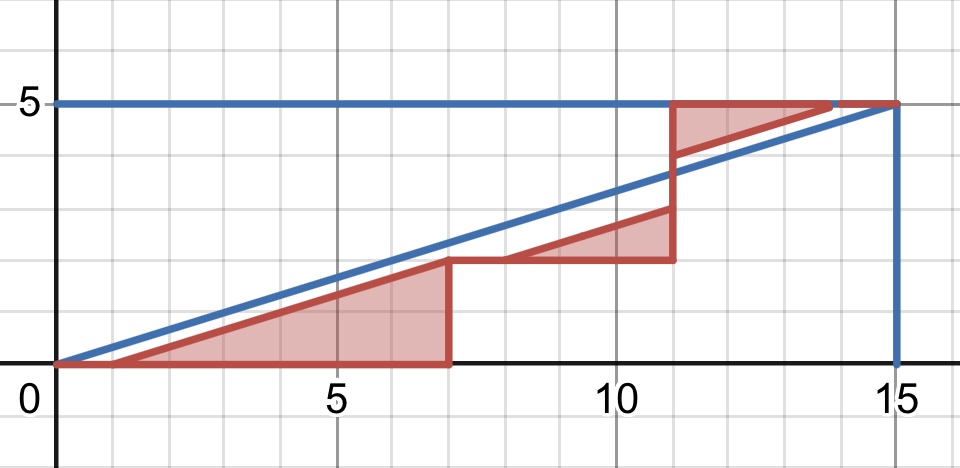パターン2
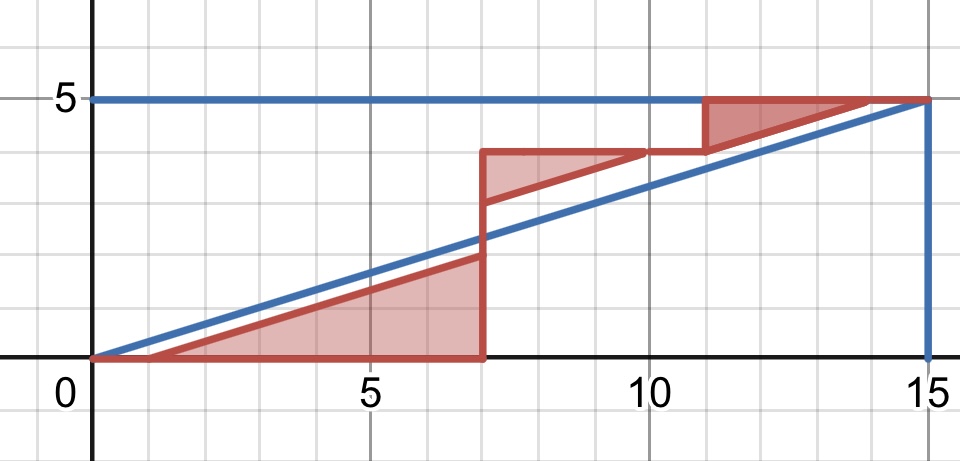パターン3
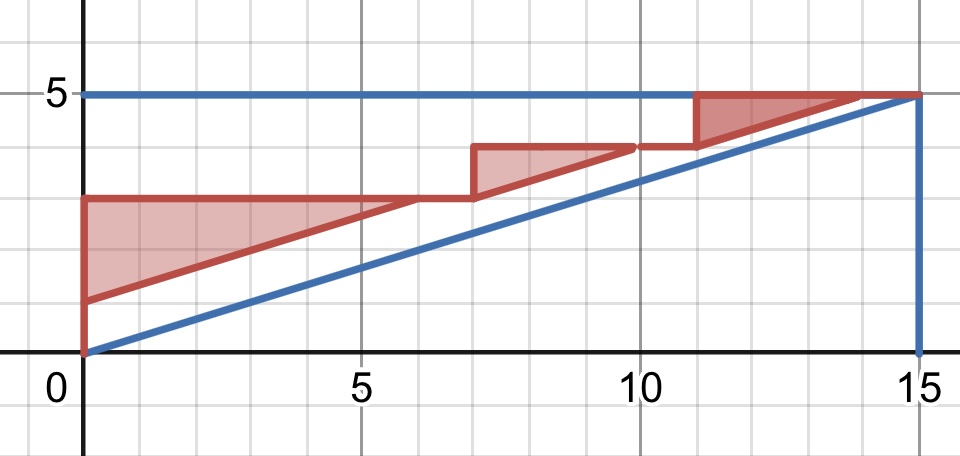パターン4

ラストパート

補題2の式を
$a_{n} := m \times \sum_{n_{1} + n_{2} + \dots + n_{m - 1} = n - 1} \frac{1}{(m - 1) n_{1} + 1} (\binom{m n_{1}}{n_{1}}) \cdot \frac{1}{(m - 1) n_{2} + 1} (\binom{m n_{2}}{n_{2}}) \dots \frac{1}{(m - 1) n_{m - 1} + 1} (\binom{m n_{m - 1}}{n_{m - 1}})$
とすると, 直線 $(m - 1) y = x$ 上の格子点を $(0, 0)$ を除いてちょうど $k$ 回通り, $((m - 1) n, n)$ へと進む経路数の総数は
$\sum_{n_{1} + n_{2} + \dots + n_{k} = n} a_{n_{1}} a_{n_{2}} \dots a_{n_{k}} = [x^{n}] (\sum_{i = 0}^{\infty} a_{i} x^{i})^{k}$
であるから, $k = 0, 1, \dots$ で総和を取ることで, $(0, 0)$ から $((m - 1) n, n)$ への経路の総数について以下の等式を得る.
$\begin{aligned} (\binom{m n}{n}) & = \sum_{k = 0}^{\infty} [x^{n}] (\sum_{i = 0}^{\infty} a_{i} x^{i})^{k} \\ = [x^{n}] \sum_{k = 0}^{\infty} (\sum_{i = 0}^{\infty} a_{i} x^{i})^{k} \\ = [x^{n}] \frac{1}{1 - (\sum_{i = 0}^{\infty} a_{i} x^{i})} \end{aligned}$
補題2より,
$\sum_{i = 0}^{\infty} a_{i} x^{i} = m x (\sum_{i = 0} \frac{1}{(m - 1) i + 1} (\binom{m i}{i}) x^{i})^{m - 1}$
したがって,
$\sum_{n = 0}^{\infty} (\binom{m n}{n}) x^{n} = \frac{1}{1 - m x (\sum_{n = 0}^{\infty} \frac{1}{(m - 1) n + 1} (\binom{m n}{n}) x^{n})^{m - 1}}$
が成立.

投稿日：1月1日

更新日：1月1日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

MARTH

3796

OMC黄

他の人のコメント

コメントはありません。

読み込み中

MARTH

組み合わせとmnCnの形式的冪級数