近畿大学数学コンテストA-5の途中を組み合わせ的に

　MARTH氏が Xで提起した問題 の組み合わせ的解釈についての自案を提示する．かなり無理矢理な解釈（と言うか計算多め）なので納得できておらず，さらなる上位解釈が現れることに期待して拙作を出しておこう，と言うやつです．
　なお問題の大元は 近畿大学の数学コンテスト の令和7年のA-5のようです．他の問題も要チェック．

　MARTH氏の解説は上述のポストもしくは こちら から確認されたし．

　組み合わせっぽい解釈に移る前に
$\displaystyle A(n)=\sum_{k=0}^{n}(-1)^k { 3n+1-2k \choose n-k } { 2n+1-k \choose k } $
$\displaystyle B(n)=\sum_{k=0}^{n-1}(-1)^k { 3n-2k \choose n-1-k } { 2n-k \choose k }$
として$A(n)$を少し計算してから解釈を与えて$B(n)$を考えていく．

• $A(n)$を少し変形する
  $\displaystyle \begin{align*} { 3n+1-2k \choose n-k } { 2n+1-k \choose k } &= \dfrac{(3n+1-2k)!}{(n-k)!(2n+1-k)!}\dfrac{(2n+1-k)!}{k!(2n+1-2k)!}\\ &=\dfrac{(3n+1-2k)!}{(2n+1-2k)!n!}\dfrac{n!}{k!(n-k)!}\\ &={ 3n+1-2k \choose n } { n \choose k } \end{align*}　$
  より，
  $\displaystyle A(n)=\sum_{k=0}^{n}(-1)^k { 3n+1-2k \choose n } { n \choose k } $
  を求めれば良い．

• $A(n)$に解釈を与える
  　理解しやすいように具体例として$n=3$の場合を考える．すなわち
  $\displaystyle A(3)={ 10 \choose 3 }{ 3 \choose 0 }-{ 8 \choose 3 }{ 3 \choose 1 }+{ 6 \choose 3 }{ 3 \choose 2 }-{ 4 \choose 3 }{ 3 \choose 3 }$
  を求めてみたい．
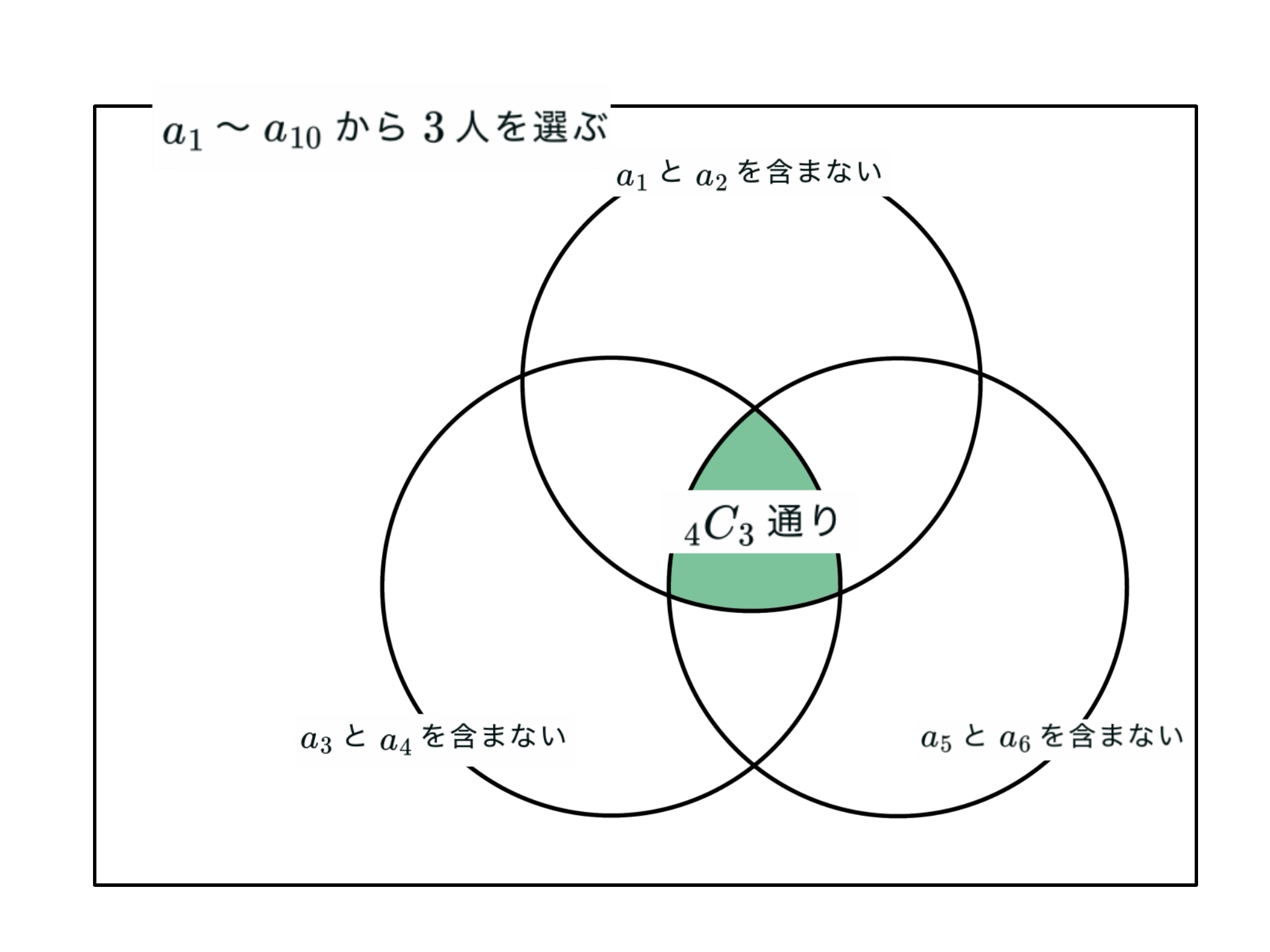
  　ここで，$a_1$〜$a_{10}$の$10$人から$3$人を選ぶ方法を考える．さらに$a_1$と$a_2$，$a_3$と$a_4$，$a_5$と$a_6$が順にカップル$1,2,3$であるとする．
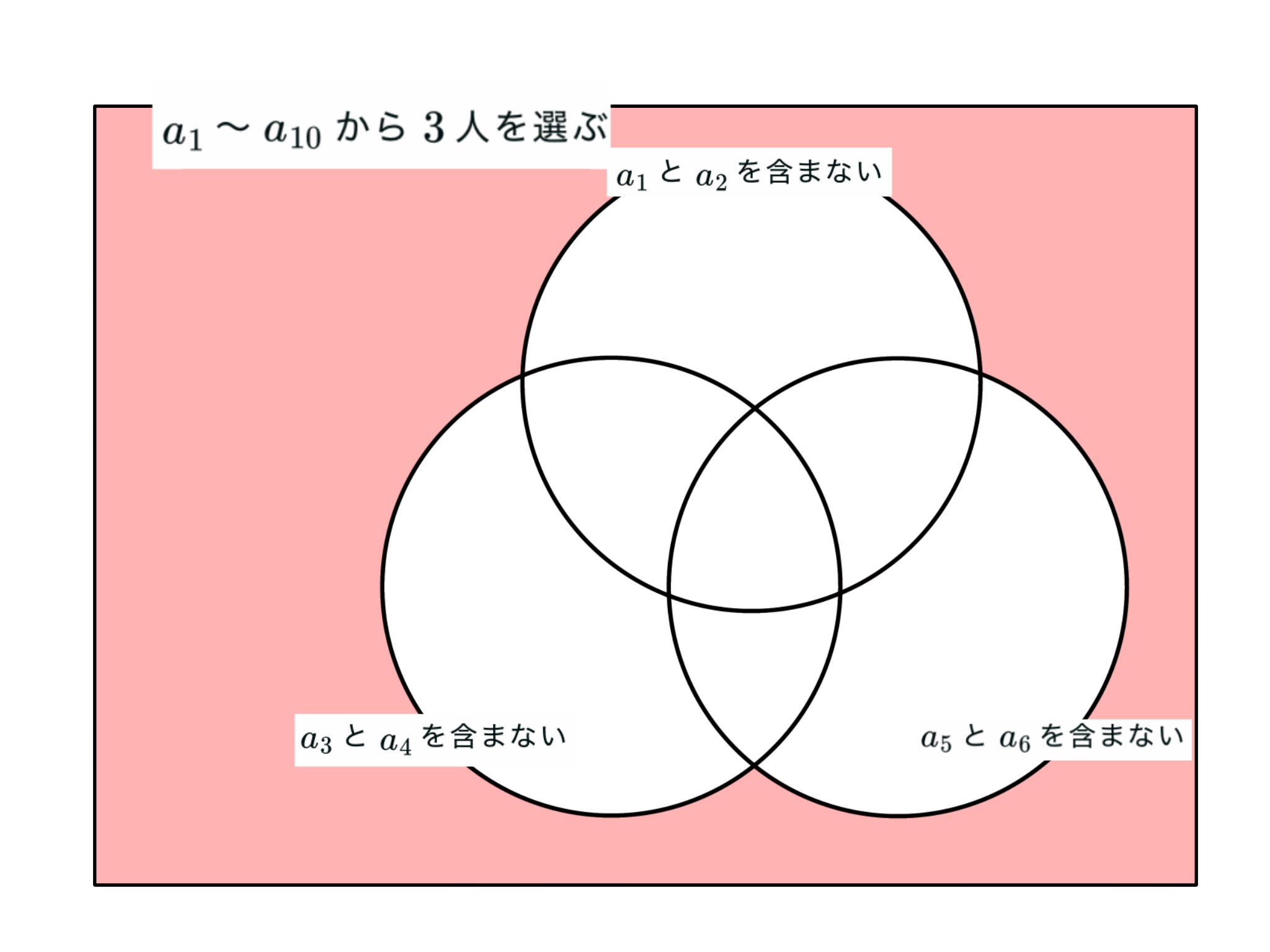  カップルの設定要らなかったか
  　上図の色がつている部分の場合の数を二通りの方法で求めたい．
  　まずは全体からド・モルガンの法則を考慮して引き算して求める．全体の場合の数はカップル$3$組から$0$組除外して残りの$10$人から選ぶ方法であり，$\displaystyle { 10 \choose 3 }{ 3 \choose 0 }$通りである．
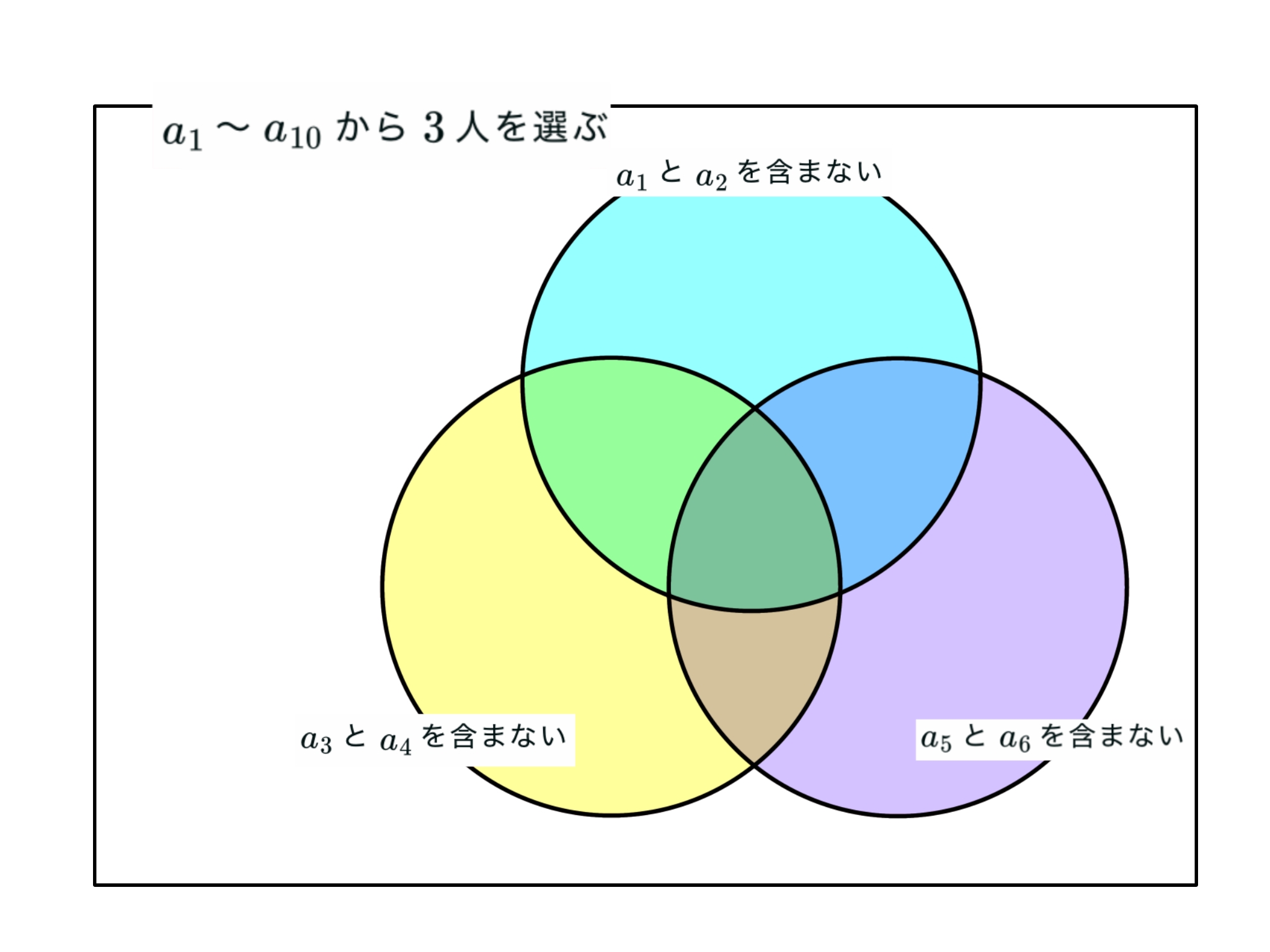  引き算する部分である和集合を考えよう
  　引き算すべき場合の数はド・モルガンの法則から，$k=1$〜$3$について除外するカップル$k$組を選び，残りの$10-2k$人から$3$人選ぶ方法を順に足し引きすることになる．したがって図$1$の領域の場合の数は$\displaystyle { 10 \choose 3 }{ 3 \choose 0 }-{ 8 \choose 3 }{ 3 \choose 1 }+{ 6 \choose 3 }{ 3 \choose 2 }-{ 4 \choose 3 }{ 3 \choose 3 }$となる．
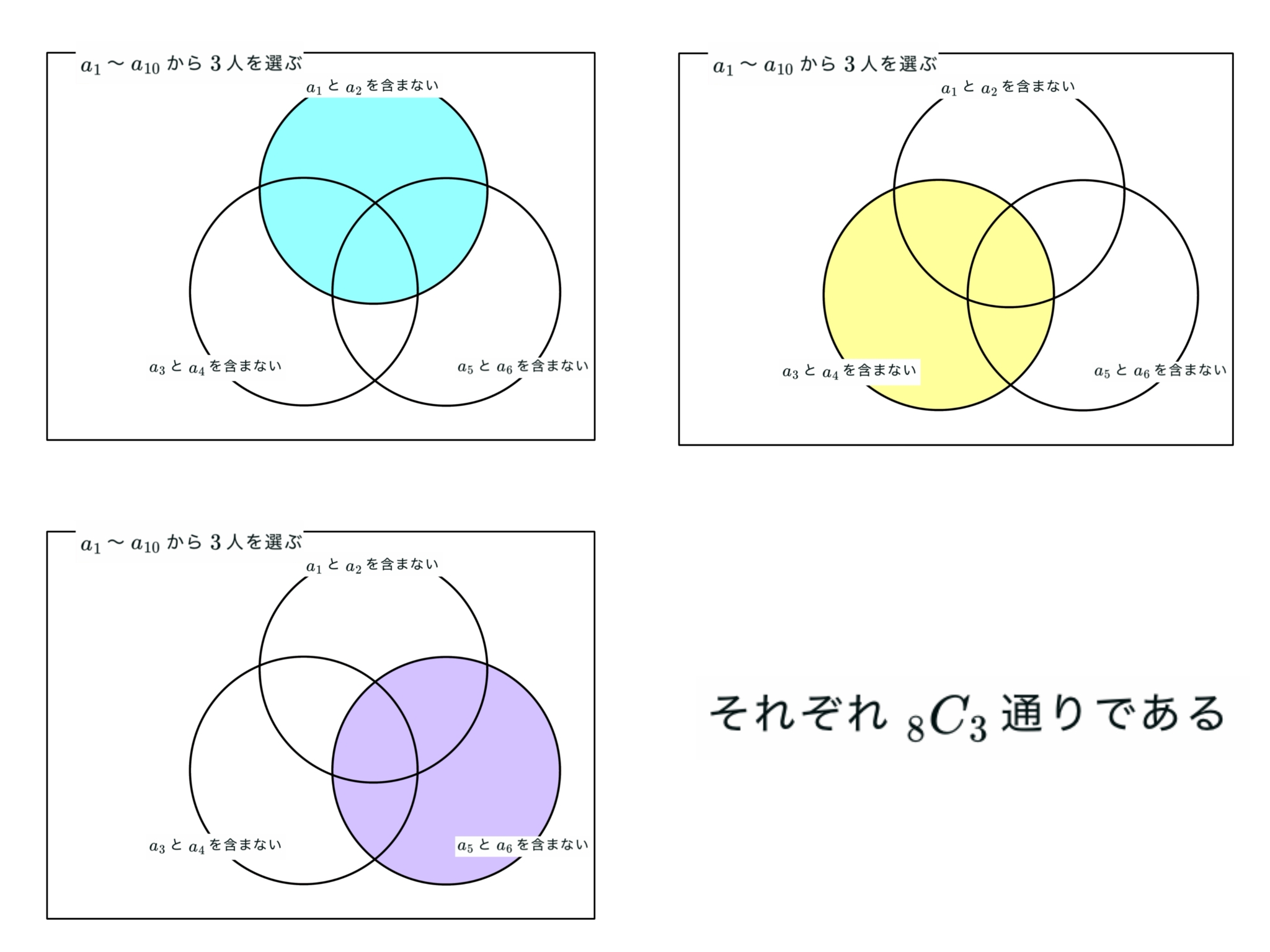  全体からこれらを引いて
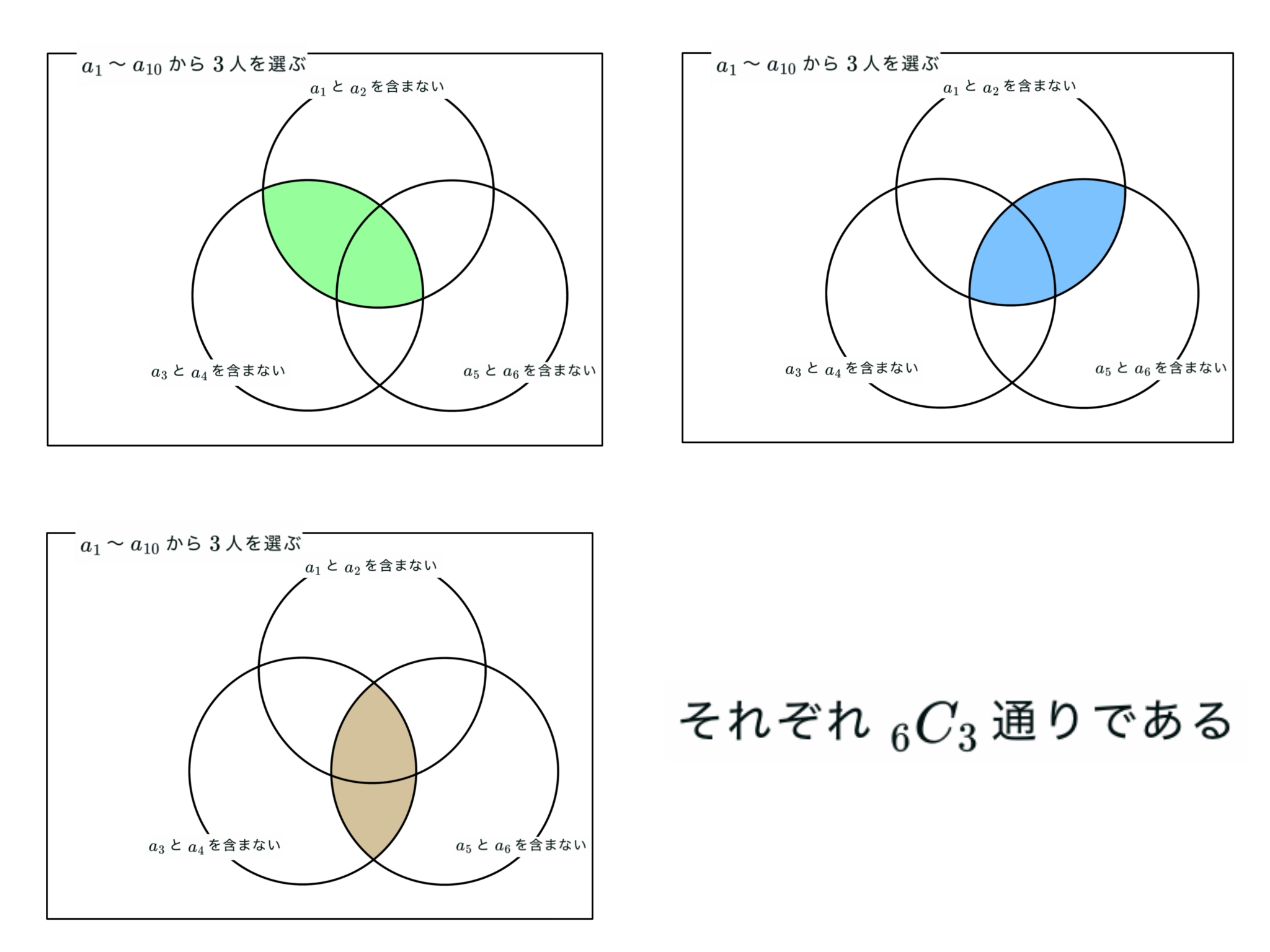  これらを足して
  これを引く

　ところで，図$1$の領域は「カップル$1$から$1$人以上」「カップル$2$から$1$人以上」「カップル$3$から$1$人以上」で計$3$人選ぶ方法なので，それぞれ$2$人のうちどちらを選ぶかで$2^3$通りとなる．したがって$\displaystyle { 10 \choose 3 }{ 3 \choose 0 }-{ 8 \choose 3 }{ 3 \choose 1 }+{ 6 \choose 3 }{ 3 \choose 2 }-{ 4 \choose 3 }{ 3 \choose 3 }=2^3$
であり，同様の議論から
$\displaystyle A(n)=\sum_{k=0}^{n}(-1)^k { 3n+1-2k \choose n } { n \choose k }=2^n $
となる．

• $B(n)$を求める
  　具体例として$n=4$の場合を考える．これは解釈というより二項係数の計算で詰めていく．
  $\displaystyle B(n)=\sum_{k=0}^{n-1}(-1)^k { 3n-2k \choose n-1-k } { 2n-k \choose k }$より$n=4$では
  $\displaystyle B(4)={ 12 \choose 3 }{ 8 \choose 0 }-{ 10 \choose 2 }{ 7 \choose 1 }+{ 8 \choose 1 }{ 6 \choose 2 }-{6 \choose 0 }{ 5 \choose 3 }$
  $\displaystyle =({ 11 \choose 3 }+{ 11 \choose 2 }){8 \choose 0 }-({ 9 \choose 2}+{ 9\choose 1 }){7 \choose 1})+({ 7 \choose 1 }+{ 7\choose 0 }){6\choose 2}-{5 \choose 0 }{ 5 \choose 3 }…①$
  ここで
  $\displaystyle {11 \choose 3 }{ 8 \choose 0 }-{9 \choose 2 }{ 7 \choose 1 }+{7 \choose 1 }{ 6 \choose 2 }-{5 \choose 0 }{ 5 \choose 3 }$
  $\displaystyle ={11 \choose 3 }{ 3 \choose 0 }-{9 \choose 3 }{ 3 \choose 1 }+{7 \choose 3 }{ 3 \choose 2 }-{5 \choose 3 }{ 3 \choose 3 }$
  は$A(3)$と同様の議論から$2^3$であり，これを繰り返せば
  $\displaystyle ①=2^3+ {11 \choose 2 }{ 8 \choose 0 }-{9 \choose 1 }{ 7 \choose 1 }+{7 \choose 0 }{ 6 \choose 2}$
  $\displaystyle =2^3+ ({10 \choose 2 }+{10 \choose 1 }){ 8 \choose 0 }-({8 \choose 1 }+{8 \choose 0 }){ 7 \choose 1 }+{6 \choose 0 }{ 6 \choose 2}$
  $\displaystyle =2^3+({10 \choose 2 }{ 2 \choose 0 }-{8 \choose 2 }{ 2\choose 1 }+{6\choose 2 }{ 2 \choose 2 })+({10 \choose 1 }{ 8 \choose 0 }-{8\choose 0 }{ 7 \choose 1 })$
  $\displaystyle =2^3+2^2+({9 \choose 1 }+{9 \choose 0 }){ 8 \choose 0 }-{7\choose 0 }{ 7 \choose 1 }$
  $\displaystyle =2^3+2^2+{9 \choose 1 }{1 \choose 0 }-{7\choose 1}{1 \choose 1 }+{9\choose 0 }{ 8 \choose 0 }$
  $\displaystyle =2^3+2^2+2^1+2^0=2^4-1$
  となり，同様の議論から$B(n)=2^n-1$が求まる．

　以上の議論から，$A(n)-B(n)=1$となる．
　もう少し直接的な組み合わせの解釈が得られたら追記していきたい．