n乗根の小数部分について

どすこい！yokodunaです。この記事は AMC2023(Advent Math Calender) の19日目の記事となっています。他の人の記事もとてもおもしろいので、ぜひ読んでください。

今回は「$n$乗根の小数部分について」というテーマで記事を書きました。私ははじめてMathlogで記事を書いたので、ところどころ見づらい点もあったかもしれませんが、どうか温かい目で見ていただけると幸いです。

1,$n$乗根の小数部分について

まず、下の問題を考えてみてください。

行間を取ります。
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
下に続きがあります。
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
答え:存在する

ここで、お気づきの人もいるかと思いますが、上のような議論で、どんな桁数のどんな並びも自然数の平方根に出てくるとわかります。また、$3$乗根でも$100$乗根でも、上の議論は適切にできることがわかると思います。
なので、下のような命題が成り立ちます。

2,$n$の$n$乗根の小数部分について

次に、下の問題を考えてみてください。

再び行間を取ります。
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
下に続きがあります。
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
$\newline$
答え:存在しない

ここで、$y$は極大値を取ったあと、単調減少するので、たとえば、$\sqrt[3]{3} \fallingdotseq1.442 $、$\sqrt[4]{4}\fallingdotseq1.414$より、$\sqrt[n]{n}=1.42\cdots$となるような自然数$n$もないとわかります。
ここで、先程の1番の議論では、$\sqrt{n}$の小数点部分は何にでもなりうるという話でしたが、$\sqrt[n]{n}$の小数点部分は限られたものにしかなり得ないという結論に至りました。形は似ているのになぜでしょう。

3,グラフの形状について

先程の疑問を、視覚的に解決させるのがグラフです。 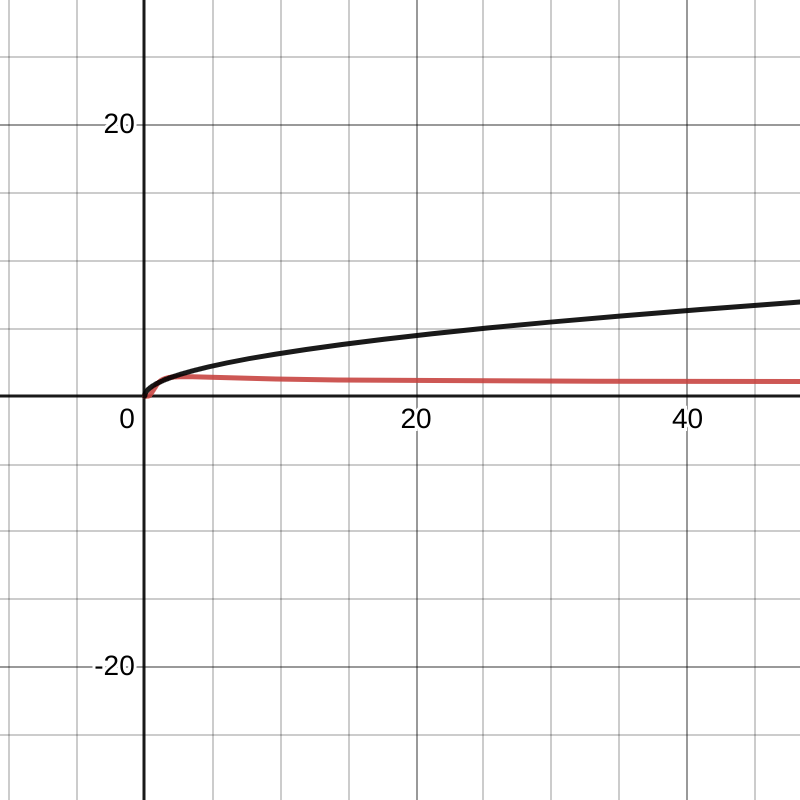それぞれの問題を表したグラフ
上の黒いグラフは、$y=\sqrt{x}$で、赤いグラフは$y=\sqrt[x]{x}$を表しています。
形状は、黒いグラフは上に向かって緩やかに伸び続けているような感じで、赤いグラフは、あるところを境に下に下がっていっていて、だんだんx軸と平行になってきているような感じです。これはまず、極大値の有無を表しており、黒い方は極大値がなく、赤い方は極大値があります。また、赤いグラフは、$x$が1以上のときに$y$も1以上になることがわかるので、赤いグラフは、いわば押しつぶされているような形状だと言えます。
ここから、黒いグラフは、上にただ伸びているグラフなので、あまり制限はないが、赤いグラフは、押しつぶされているグラフなので、$\sqrt[2]{2}$,$\sqrt[3]{3}$,$\cdots$の整数部分がすべて同じで、しかも途中からその値が小さくなり続けるというふうな制限がつくというふうに考えて、感覚的に問題の結論の違いが体感できると思います。また、下に記すグラフソフトをいじると、$\sqrt[n]{n}$は何倍しても小数部分は限られて、指数のところを何倍してもそれは同じだということがわかると思います。
https://www.desmos.com/calculator/wj27zebz1h

4,おわりに

ここまで読んでいただいた皆様へ大変感謝いたします。
なにか意見などがあれば、ぜひコメントに書いてください。(特に、最初の問題1の具体的な$n$の値などがわかった方がいらしたら、ぜひ書いていただきたいです。)