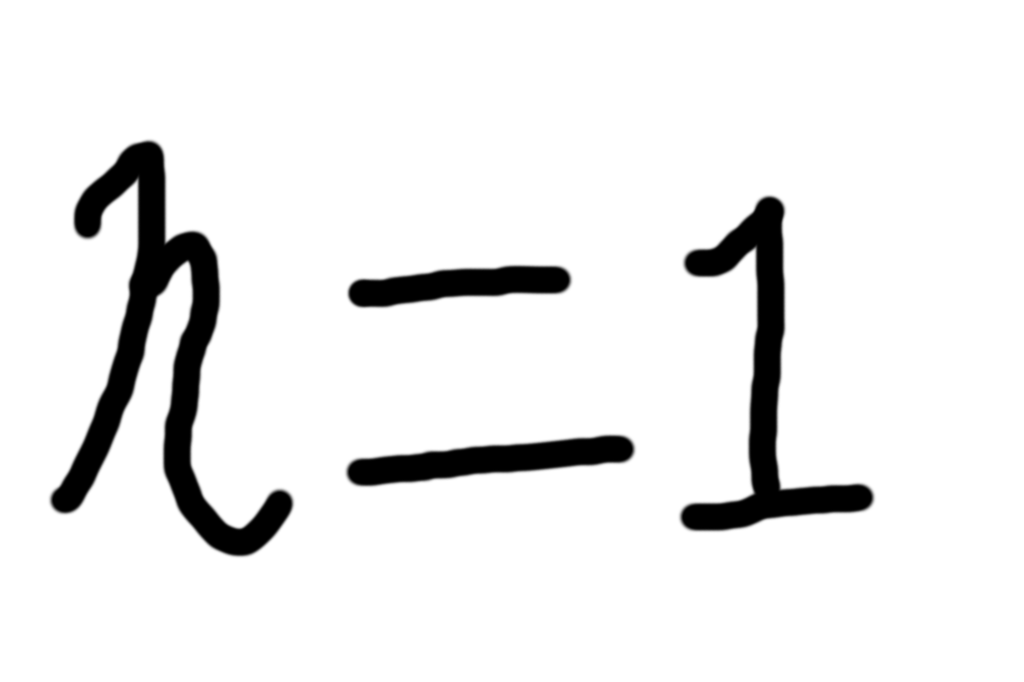0~1の総和

はじめに

　こんにちはn=1です。今回は、積分しているときに思いついた0~1の総和について書いていきます。

0~1の総和について

　今回の記事では0～1の総和を$0+1$ではなく、0～1の間の有理数すべての和とします。

準備

　まずは0~1の和を数を分割して求めます。0,0.5,1の三分割で考えるとまず0を考えずに
$0+0.5+1=0.5+1$
最小の有理数の分母をかけると全部整数になり楽なのでかけ元に戻すと
$0.5+1=\frac{1}{2}+1=\frac{1}{2}(1+2)= \frac{3}{2}$
同じように四分割も
$0+\frac{1}{3}+\frac{2}{3}+1=\frac{1}{3}(1+2+3)=2$
　以上よりn+1分割の時は
$0+\frac{1}{n}+\frac{2}{n}+\cdots+ \frac{n-1}{n}+1= \sum_{k=0}^{n} \frac{k}{n}= \frac{1}{n} \sum_{k=1}^{n}k= \frac{n(n+1)}{n\cdot2}= \frac{n+1}{2}$
となります。

本題

　では本題の0～1の総和ですが、0～1を無限分割した和と考えられるので
$ \lim_{n \to \infty}0+\frac{1}{n}+\frac{2}{n}+\cdots+ \frac{n-1}{n}+1=\frac{n+1}{2}=\infty$
となるので0～1の総和は$\infty$という結果が得られました。

最後に

　今回の記事を書いて0～1の有理数をとると、当然有理数は可算無限なので当たり前なことに気づきました。そして総和の$k$を関数$f(k)$という風にすればその関数の0～1の総和が求まり($⌊x⌋$など一部以外は発散する)、$f(\frac{k}{n})$にすれば積分になるなーと思いました。
　以上で今回の0~1の総和は終わりです。一部不適当な表現が含まれており、誠に申し訳ございませんでした。投稿を見てくださりありがとうございました。