重みつきカタラン数の不思議な性質とその応用
はじめに
こんにちは。Hiroです。今回はPhysics Lab.アドベントカレンダーの記事として重みつきカタラン数に関する性質について紹介しようと思います。
重みつきカタラン数って何だよって感じですが、これは僕の勝手な命名です。カタラン数のそれぞれの経路にその階層に付随した重みをつけてあげて足し合わせると、とても綺麗な構造が現れることに気がつき、今回の記事を書きました。主張自体は小学生でも理解できるくらいの内容ですので、様々な方に見ていただけると嬉しいです。
またPhysics Lab.なのに算数じゃん!って思う方もいるかもですが、このトリックが実は量子力学のいくつかの場面で有効活用できることを紹介したいと思います。
モチベーションと命題
今回考えたいのは以下のような図形を、回り道をせずに左から右に動いていく状況です。その時に以下のように各格子点にそこまでの経路の数を記録していくことにします。
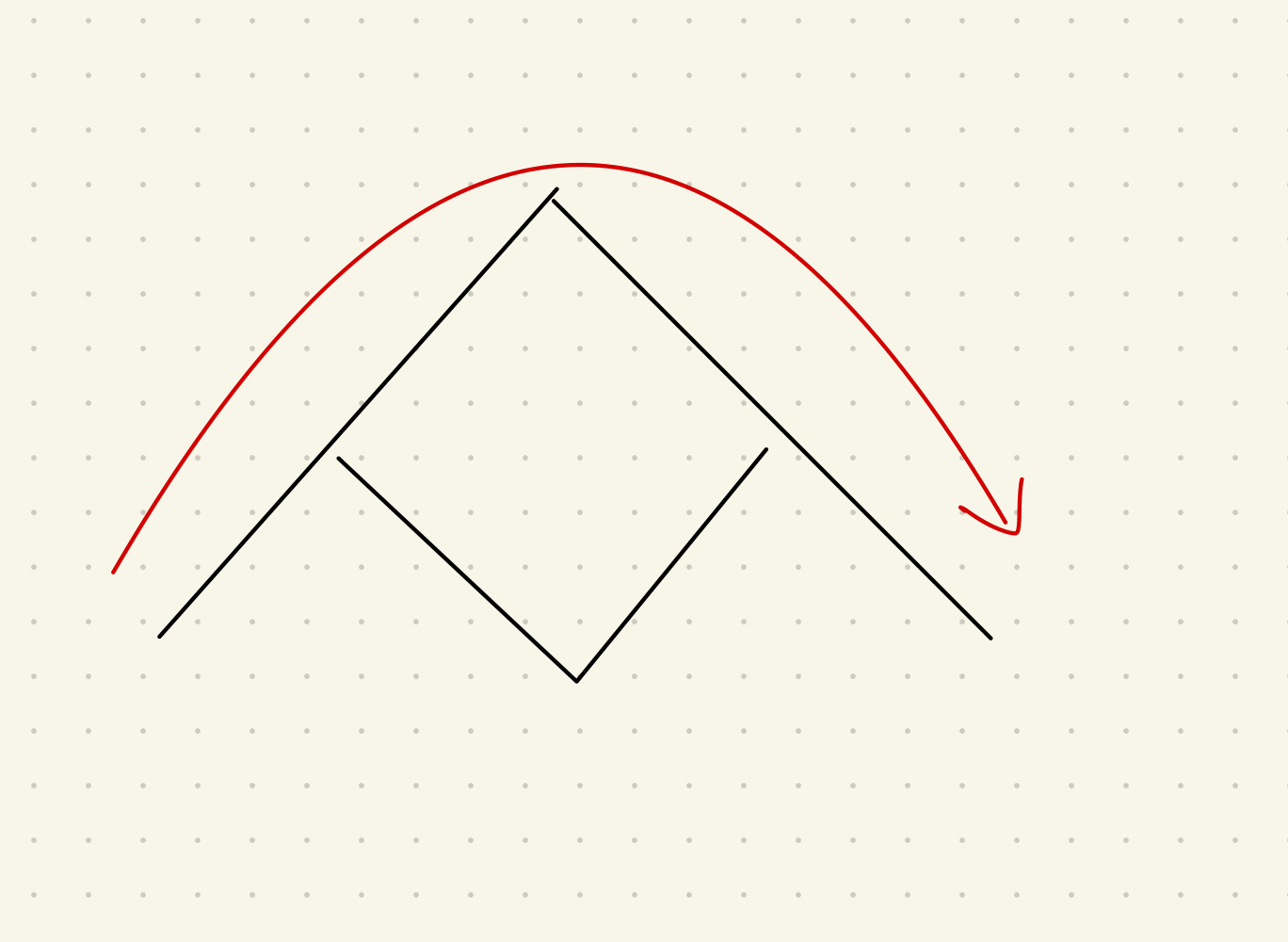 セッティング
セッティング
普通にこの経路のパターンを足し合わせていくと、いわゆるカタラン数になるのは皆さんご存知だと思います。
(wikipediaのカタラン数のページ)
ではここに以下のようなルールを付け足してみましょう。
上に登るときに、そこまでの経路の数に、段数を掛け算した値を進んだ先に記録する。
先ほどの例にこれを適用すると以下のようになります。
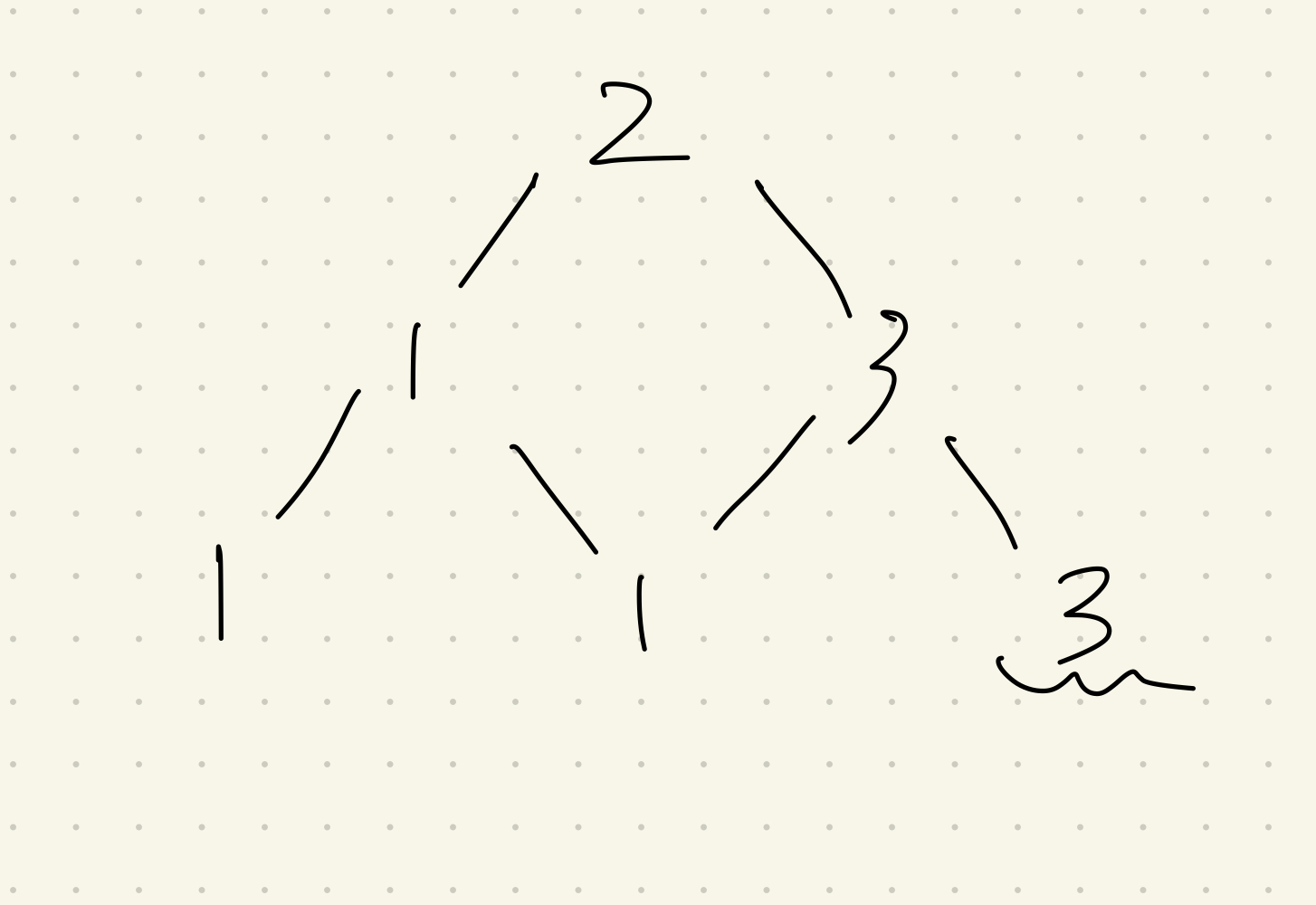 数を書き込むとこう
数を書き込むとこう
他の段数ではどうなのでしょうか?試しに$1\sim 4$で書き下してみると...?
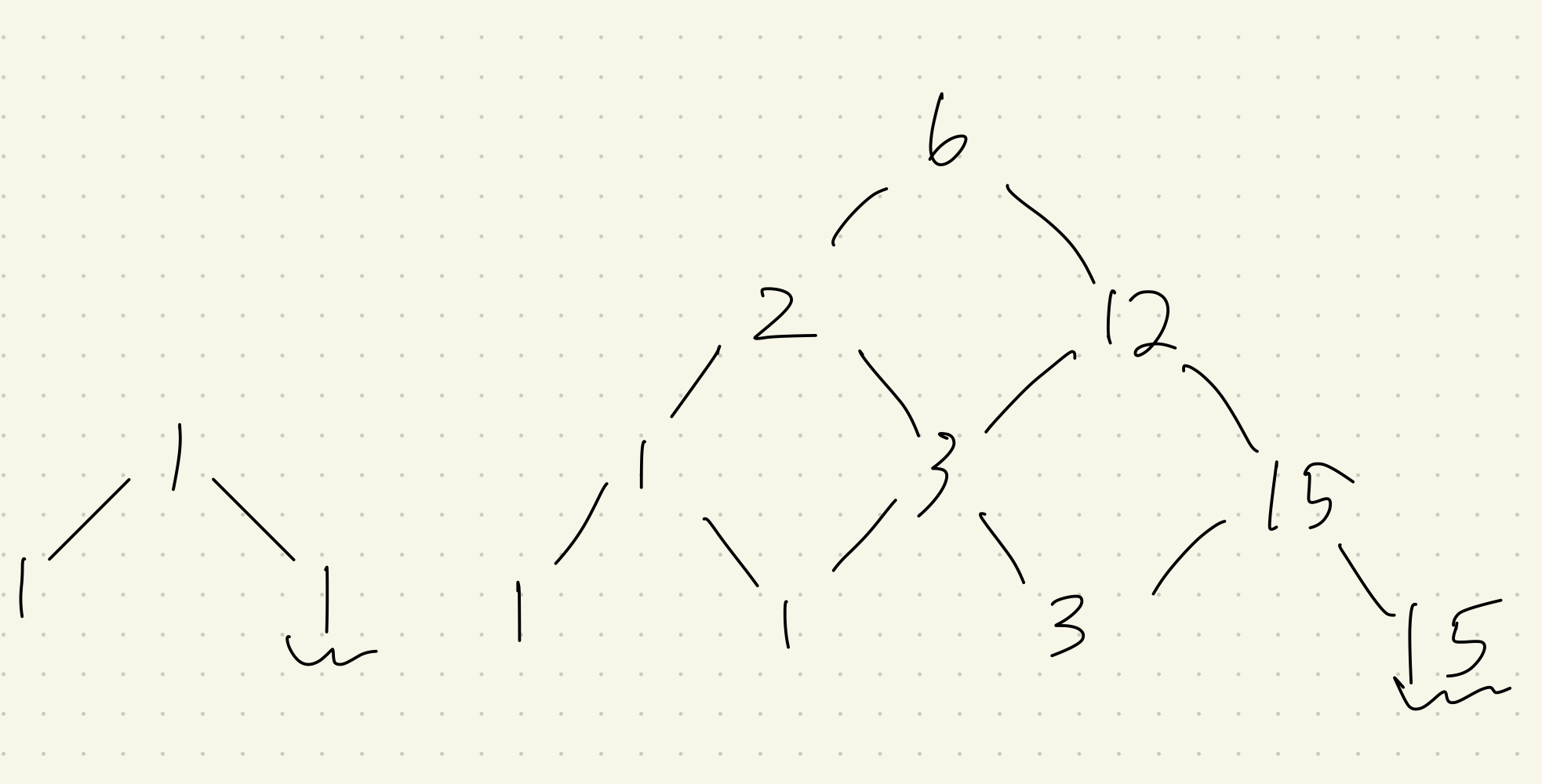 段数が1,3
段数が1,3
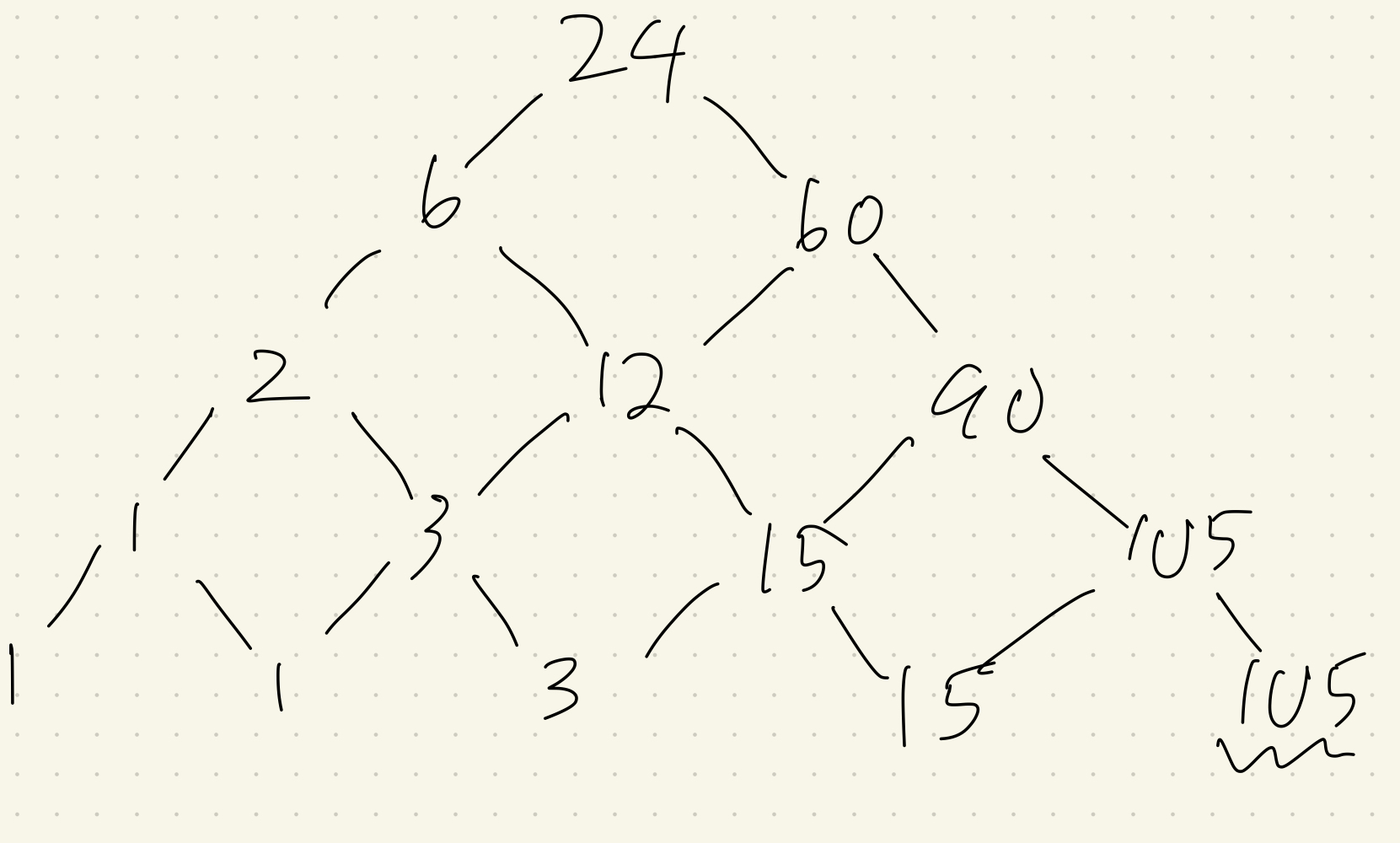 段数が4
段数が4
ぱっと見ですが、奇数のみの掛け算になっていそうです。
実は、この値は段数を$n$とした時に$(2n-1)!!$になります。以下で、初等的な帰納法を用いてこれを証明していきます。
証明のアプローチ
頂点のグループ分けと重み付け
経路の各時点 $m$ ($m=1 \sim 2n+1$) における状態によって頂点をグループ分けする。
表記として、$\{a_n\}_m$ を「$n$ ステップ目において、高さが$m$の状態にある経路の重みの和」のような量として定義する。
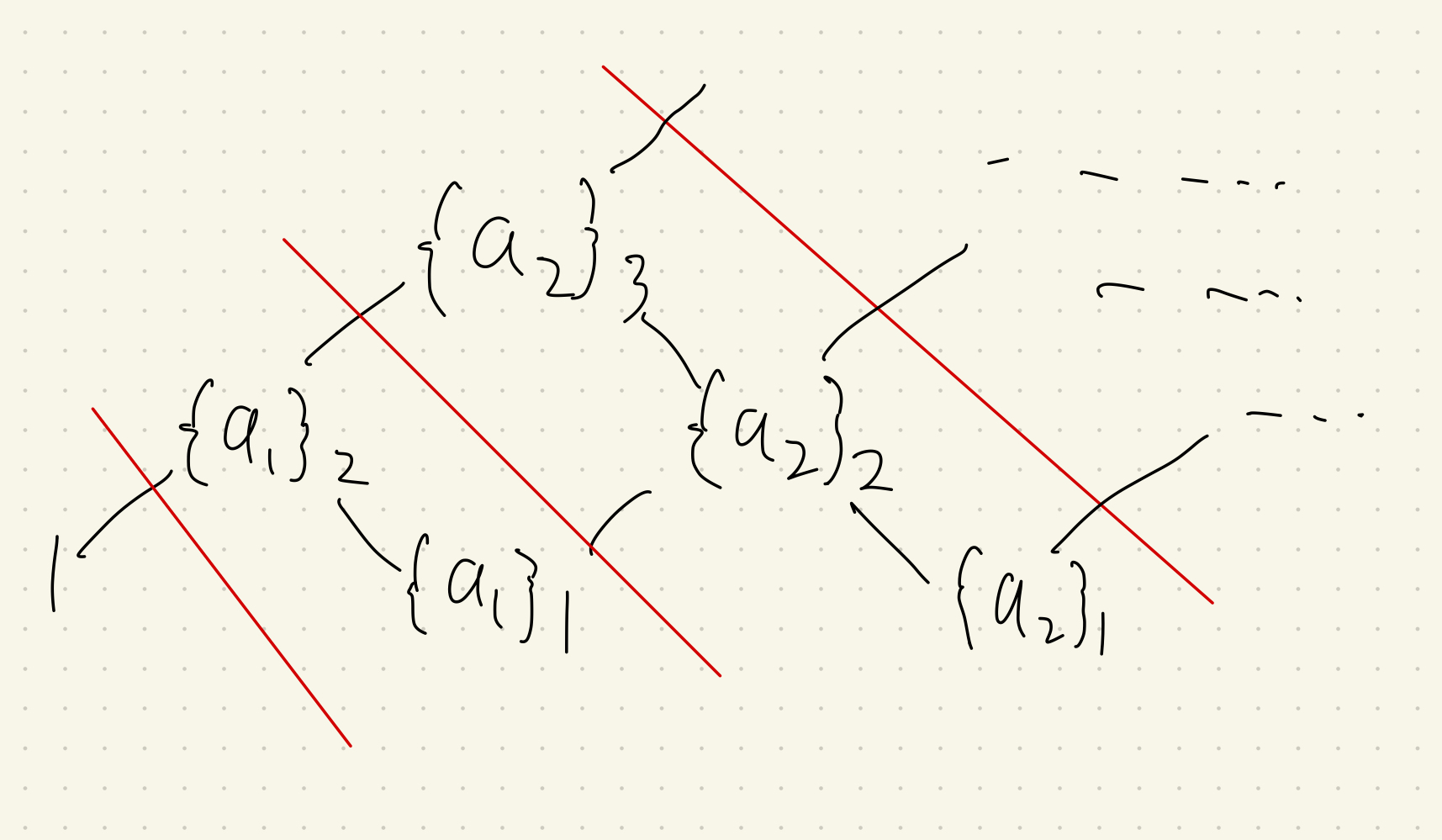 命名ルール
命名ルール
$\{a_n\}_1=(2n-1)!!$
証明
以下の再帰的なルールが成立することが簡単にわかる。
$N\geq1$について
- $\{a_1\}_1=\{a_1\}_2=1$
- $\{a_{N+1}\}_{N+2}=(N+1)\{a_{N}\}_{N+1}$
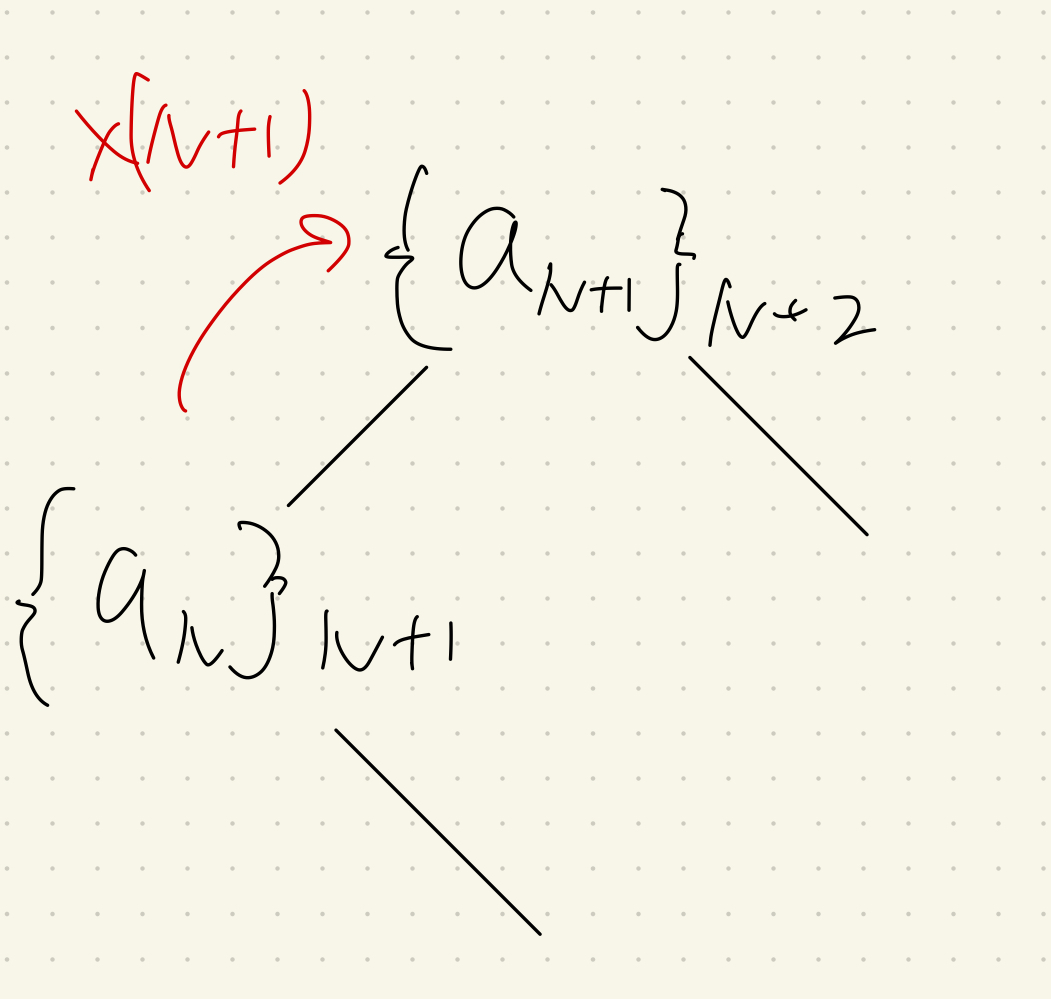 ルール2
ルール2
- $\{a_{N+1}\}_{k(\neq N+2,1)}=(k-1)\{a_{N}\}_{k-1}+\{a_{N+1}\}_{k+1}$
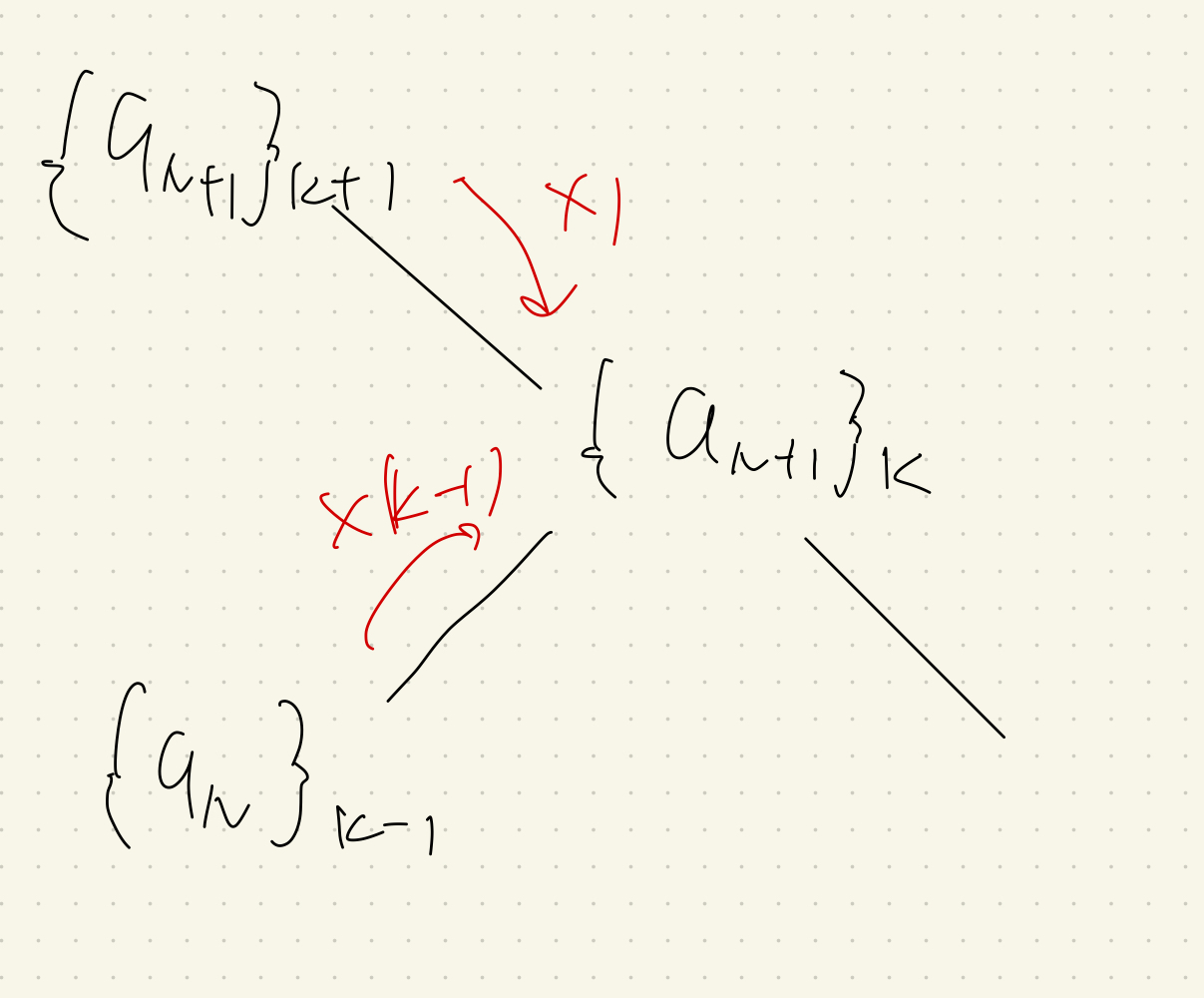 ルール3
ルール3
- $\{a_{N+1}\}_1=\{a_{N+1}\}_2$
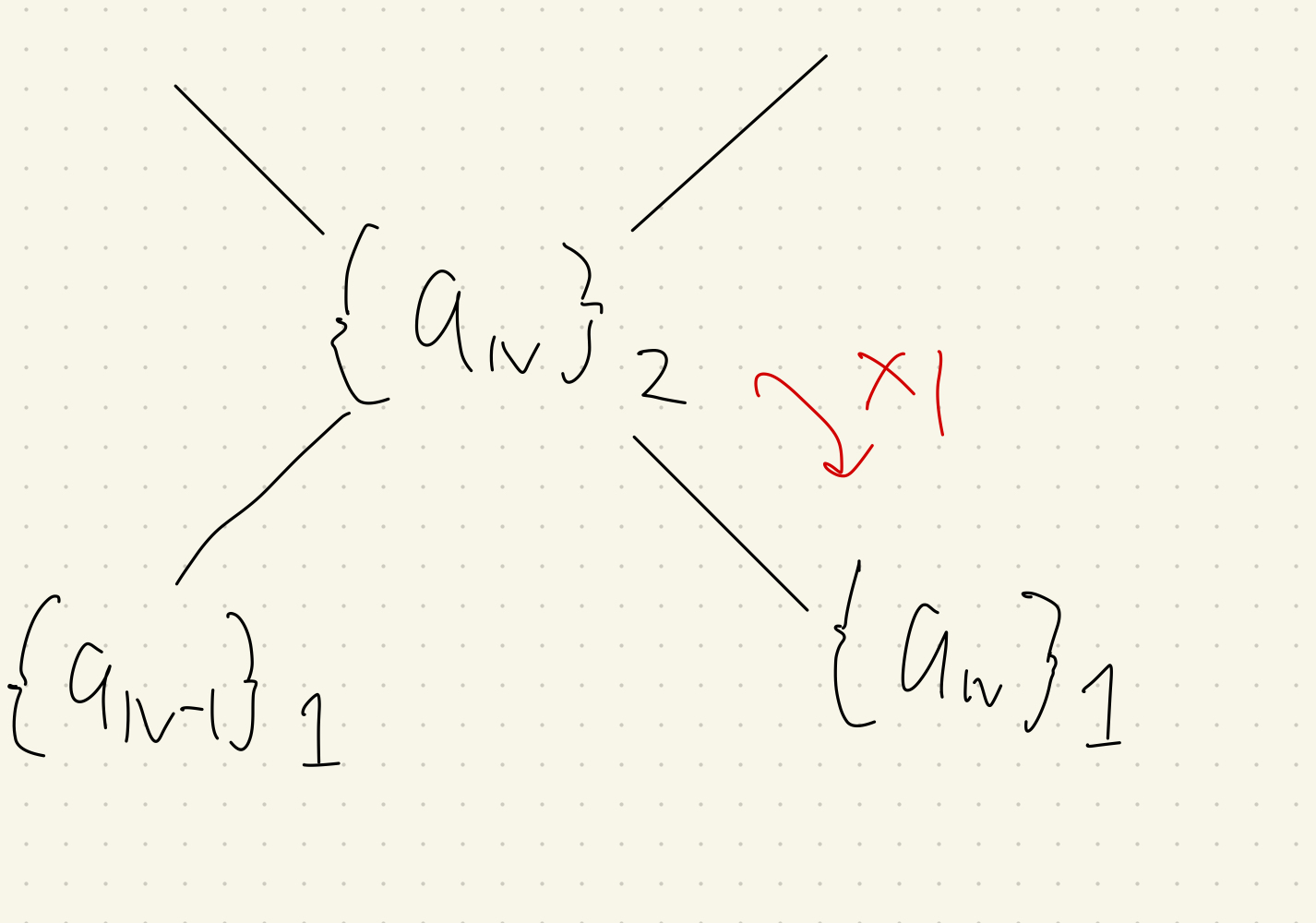 ルール4
ルール4
ここで計算を簡略化するため、命題を包含する以下の補題を帰納法を用いて証明する。
数列 $\{a_N\}_k$ に対して、以下の関係が成り立つ。
\begin{equation}
\{a_{N+1}\}_k = \{a_N\}_{k-1} \times (2N + 3 - k)
\end{equation}
補題の証明
2段階の帰納法を用いる。
1. 小さな $N$ での確認
最初に例示した図を見ると、$N=4$までで成立していることが確認できる。
2. 帰納法のステップ
グループ $a_N$ までで補題が成立していると仮定し、次のステップ $a_{N+1}$ について考える。ここで添え字$k$に関する帰納法を同時に考える。
$k=N+2$においては、上記のルールにより
$\{a_{N+1}\}_{N+2}=(N+1)\{a_{N}\}_{N+1}=\{a_N\}_{N+1}\times (2N + 3 - (N+2))$
なので自明に成立している。
$k\geq l+1$で成立している時、$k= l$の場合を考える。
ここで以下の図式を用いて、経路の合流を考える。
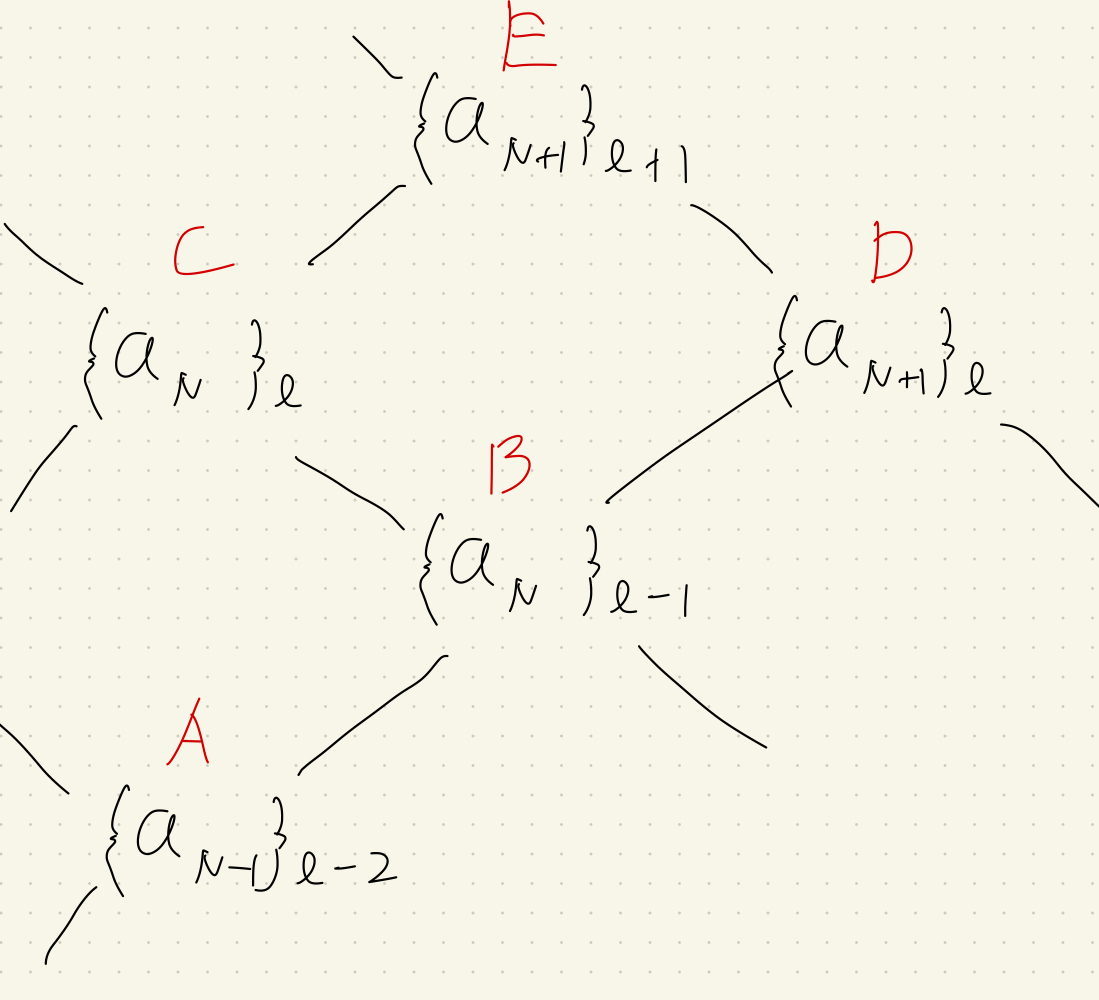 アルファベットが以下の数式と対応している
アルファベットが以下の数式と対応している
すると、上で示した関係式と帰納法の仮定から自然に
\begin{align}
B &= A \times (2(N-1)+3-(l-1)) \\
&= A \times (l-2) + C \\
\rightarrow
C &= A \times (2N+4-2l) ,\\
E &= C \times (2N+3-(l+1)) \\
&= A \times (2N+4-2l) \times (2N+2-l)\\
&= B \times (2N+4-2l),\\
D &= B \times (l-1) + E \\
&= B \times (2N+3-l)\\
\end{align}
以上により、$k$についての帰納法が成立し、その結果$N$についての帰納法も成立するので、全ての$k,N$について補題が成立することが示された。
最後に$\{a_{N+1}\}_1=\{a_{N+1}\}_2$を用いると、補題より
$\{a_{N+1}\}_1 = \{a_{N+1}\}_2 = \{a_N\}_1 \times (2N + 3 - 2)=\{a_N\}_1 \times (2N + 1)$
となるので、初期条件から$\{a_n\}_1=(2n-1)!!$が成立する。
物理学への応用
今回設定した計算規則は量子力学における生成消滅演算子$ \hat{a}^\dagger,\hat{a}$の計算規則に(おおよそ)一致しています。生成消滅演算子に関する具体的な説明は省略しますが、簡単にいうと空間に粒子を生み出したり、粒子を消したりする操作を表す演算子です。その計算ルールは真空$|0\rangle$と呼ばれる、粒子が一つもない状態を基準にして以下のようになります。
$ |n\rangle$を粒子が$n$個ある状態とした時、
- $\hat{a}|n\rangle=\sqrt{n}|n-1\rangle$
- $\hat{a}^\dagger|n\rangle=\sqrt{n+1}|n+1\rangle$
重みつきカタラン数の話の時には$|0\rangle$に対応する状態を一段目と数えていたことに気をつけましょう。このルールでは、生成消滅演算子をペアにして作用させると、
$\hat{a}^\dagger\hat{a}|n\rangle=n|n\rangle$
となります。このように元の状態まで戻ってくる操作に倍率がかかる構造が先ほどの重みつきカタラン数に似ていると思いませんか?
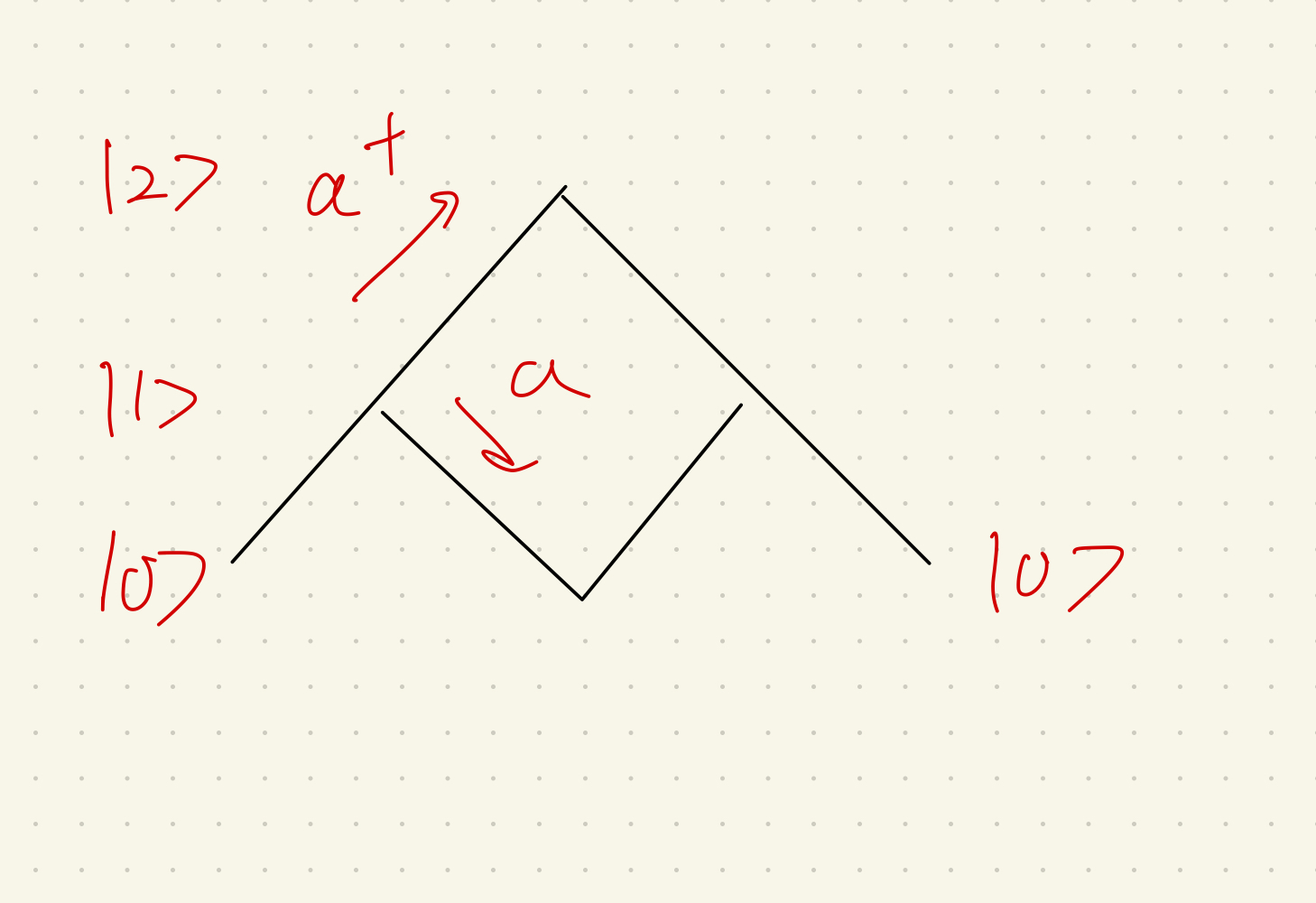 こんな感じかな?
こんな感じかな?
実は生成消滅演算子による計算ルールは、元の状態に戻ってくるという過程のもとで完全に重みつきカタラン数の議論と一致しているのです。
これは例えば摂動論において一次摂動の計算をする時に生きてきます。ハミルトニアン
$H=H_0+\lambda \hat{x}^{2n}$
の形を考えた時に、エネルギーの一次摂動に
$\langle0|\hat{x}^{2n}|0\rangle$
の項が現われます。ここで、係数を無視した時に
$\hat{x}\propto(\hat{a}^\dagger+\hat{a})$であるので、$\hat{x}$が一回かかるごとに、生成演算子か消滅演算子のどちらかがかかるわけですが、式の形から最終的には真空に戻ってこなくてはなりません。これは高さが$n$の重みつきカタラン数を数えることと等価になります。そのため、一次摂動の係数は
$(2n-1)!!$
と一瞬で計算が可能なのです。
実際$n=1,2,3$などはよく出てくるパターンだと思いますが、それぞれ$1,3,15$と馴染みのある値が出てくるのではないでしょうか。また状態に対する一次摂動などで出てくる
$\langle0|\hat{x}^{2n}|m\rangle$
のような状態も、今回途中で示した補題を使ってあげれば簡単に計算することが可能になります。
終わりに
今回はちょっと不思議な性質を持つ、重みつきカタラン数について、駆け足ではありましたが紹介しました。今回紹介した摂動論のほかにも、$e^{(\hat{a}e^{i\omega t}+\hat{a}^\dagger e^{-i\omega t})}$のような形状の演算子に関する期待値を求めるときなどにもこの手法は役に立ちます。
皆さんも勉強の中で、同じ構造を持つ対象を見つけたら、ぜひコメントで教えてください!
