【中高生向け】結局、微分って
はじめに
こんにちは. この記事では, 微分を一通り学んで計算はできるけどどうも腑に落ちない...という方, 微分って結局なんなんだろう？と思っている方に, 「お気持ち」を説明することを目的としています.
${}$
微分とは近似である
さて, 関数$f(x)$が与えられたとき, そのグラフの全体像をパッとイメージすることは困難ですが, そこで逆に, ある値のごく周辺のみをクローズアップすることを考えてみましょう. すると, $f(x)$がある程度「滑らか」なら, 十分拡大すればグラフはほぼ直線になることがイメージできると思います.
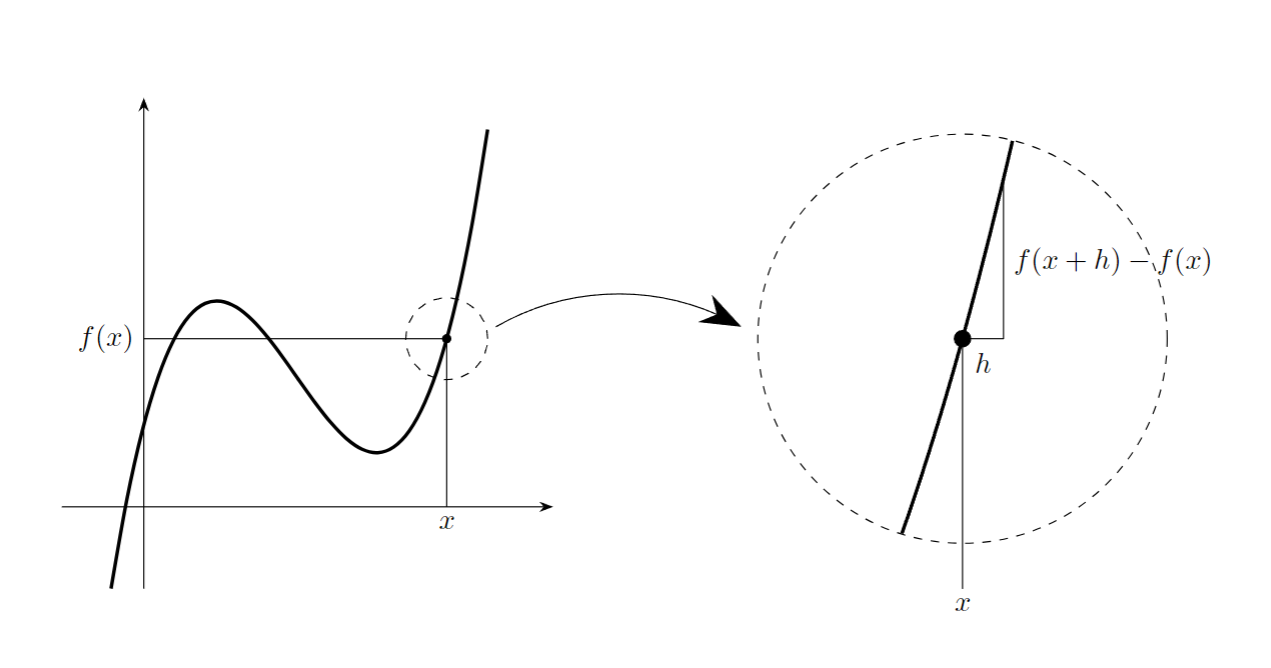クローズアップする
上図のように, （$h$が十分小さければ）$x$が$x+h$に増えるときの$f(x)$の変化量はほぼ$h$に比例すると近似できます. つまり, $h$の式として
$$ f(x+h)-f(x) \fallingdotseq \boxed{\phantom{ho}} \,h$$
のようにかけるはずです. ただし$\boxed{\phantom{ho}}$はクローズアップして直線に近似したときの傾きで, $f$と$x$ごとに決まる値です.
つまりこの$\boxed{\phantom{ho}}$は$x$の関数になりますから, $f'(x)$と書くことにしましょう.
関数$f(x)$の微分とは,
$$ f(x+h) \fallingdotseq f(x)+f'(x)h$$
という近似のことである.
ただしこの近似は, 「$h^{1\text{より大}}$程度の誤差は無視する」という意味での近似です.
この定義は普通の教科書とは違うと思いますが, このように定義の仕方を変えることにより色々な見方をするというのを数学ではよくします.
${}$
微分係数を求める
ではこの微分係数$f'(x)$は具体的にはどう求めればいいでしょうか？上の式を整理すると
$$ f'(x)\fallingdotseq\frac{f(x+h)-f(x)}{h}$$
となります. もちろんこれは近似であり等号は成り立ちませんが, $h$が小さいほど誤差が少ないことを考えれば, $h\to0$の極限をとれば等号になることが期待されます.
これはきちんと説明すると, 定義式の誤差は$h^{1\text{より大}}$程度であり, 上式はそれをさらに両辺$h$で割ったので誤差は$h^{0\text{より大}}$程度になっています. そこで$h\to0$の極限をとれば誤差は無くなります.
$$ f'(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}$$
${}$
微分公式を証明する
上の定義
$$ f(x+h) \fallingdotseq f(x)+f'(x)h$$
を用いて, 微分公式を示してみましょう.
$$ \big(f(x)g(x)\big)'=f'(x)g(x)+f(x)g'(x)$$
定義に従って変形していきます. 分かりやすいように$h$の係数にハイライトをつけます.
\begin{align*}
&f(x+h)g(x+h) \\[5pt]
\fallingdotseq&\ \bigl(f(x)+\colorbox{lightblue}{$ f'(x)$}\,h\bigl)\big(g(x)+\colorbox{lightblue}{$ g'(x)$}\,h\big)\\[5pt]
=&\ f(x)g(x)+\colorbox{lightblue}{$ f'(x)g(x)$}\,h+\colorbox{lightblue}{$ f(x)g'(x)$}\,h +f'(x)g'(x)h^2\\[5pt]
\fallingdotseq&\ f(x)g(x)+\big(\colorbox{lightblue}{$ f'(x)g(x)+f(x)g'(x)$}\big)h
\end{align*}
最後の行のハイライト部分が微分係数なので, これで示せました. ただし$h^2$は無視したことに注意します.
${}$
$$ \big(f(g(x))\big)'=f'(g(x))g'(x)$$
まず,
$$ f(g(x+h))\fallingdotseq f\Big(\colorbox{lightgreen}{$ g(x)$}+\colorbox{lightblue}{$ g'(x)h$}\Big)$$
これの右辺と
$$ f(\colorbox{lightgreen}{$x$}+\colorbox{lightblue}{$h$}) \fallingdotseq f(\colorbox{lightgreen}{$x$})+f'(\colorbox{lightgreen}{$x$})\colorbox{lightblue}{$h$}\qquad \cdots \bigstar$$
の左辺を見比べると, 似ていますね. ★式の$x$を$g(x)$に, $h$を$g'(x)h$に置き換えることで
$$ f\Big(\colorbox{lightgreen}{$ g(x)$}+\colorbox{lightblue}{$ g'(x)h$}\Big)\fallingdotseq f(\colorbox{lightgreen}{$ g(x)$})+f'(\colorbox{lightgreen}{$ g(x)$})\colorbox{lightblue}{$ g'(x)h$}$$
これの右辺の$h$の係数を見て, 示せました.
${}$
具体的に計算する
この方法は具体的な計算にも応用できます.
$f(x)=\dfrac{1}{x}$の微分係数を求めよ.
定義どおり,
$$ \frac1{x+h} \fallingdotseq \frac1{x}+ah$$
となる$a$を求めれば良いです. 両辺に$x+h$を掛けて
\begin{align*}
1\fallingdotseq&\ \Big(\frac1{x}+ah\Big)(x+h)\\[5pt]
=&\ 1+ \frac{h}{x}+axh+ah^2\\[5pt]
\fallingdotseq&\ 1+\Big(\frac1{x}+ax\Big)h
\end{align*}
よって$h$の係数が$0$でないといけないので, $a=-\dfrac1{x^2}$となります.
${}$
$f(x)=\sqrt{x}$の微分係数を求めよ.
$$ \sqrt{x+h} \fallingdotseq \sqrt{x}+ah$$
となる$a$を求めます. 両辺2乗して
\begin{align*}
x+h\fallingdotseq&\ \big(\sqrt{x}+ah\big)\\[5pt]
=&\ x+2\sqrt{x}ah+a^2h^2\\[5pt]
\fallingdotseq&\ x+2\sqrt{x}ah
\end{align*}
これの$h$の係数が一致するので, $a=\dfrac1{2\sqrt{x}}$となります.
${}$
まとめと補足
微分とは, 近似である. という意味を実感して頂けたでしょうか. $\fallingdotseq$を使って多少曖昧にした代わりに, 非常に直感的な式変形で様々な公式を示すことができました.
ちなみに, 大学以降ではこの記事のような定義を主流にすることが多いです. （厳密には$f(x+h)=f(x)+f'(x)h+\varepsilon(h),\quad \varepsilon(h)/h\to0(h\to0)$のようにします. ）この理解をしていると, 複素正則関数の定義なども分かりやすくなります.
それでは, 最後まで読んでくれた方, ありがとうございました.