文献あり

高専基礎数学の体験談と高校数学との違い

352

(この記事は2024年9月に投稿されましたが、より分かりやすく的確にするため、2025年1月に記事の大規模更新を行いました。)

まえがき

皆さんはじめまして。本記事が私の初めての投稿になるかと思います。
簡単に自己紹介をしますと、私は高等専門学校(以下, 高専)の学生で、専門に学んでいる分野は工学です。
高専では工業分野に必要な知識を学ぶため、数学のカリキュラムは、一般的な高校数学とは大きく違います。
そこで、本記事では(おおよそ)高校数学に相当する、高専の1年生基礎数学における体験談と、高校数学とどのように違うかを解説します。
本記事は高専に入学予定の方を対象としていますが、それ以外の方も読んでいただけると幸いです。

教科書は、森北出版高専テキストシリーズ基礎数学第2版に準じます。(ただし、それ以外の教科書でも十分に本記事と整合性があるはずです)
なお、学年は1年生を想定しています。

カリキュラムの構成

1年生で扱う基礎数学の内容は次の通りです。(東京高専の場合)

前期(1Q, 2Q)

複素数(数II)
整式の展開・因数分解(数I)
分数式, 整式の除法, 剰余の定理・因数定理(数II)
2次方程式, 高次方程式, 色々な方程式(数II)
集合と命題(数I)
恒等式, 等式・不等式の証明(数II)
2次関数とそのグラフ(数I)
2次関数と2次不等式・2次方程式(数I)
関数とそのグラフ(主に平行移動, 対称移動, 偶関数と奇関数), べき関数(数II・III)
分数関数, 無理関数, 合成関数, 逆関数(数III)
指数の拡張, 指数関数, 指数方程式・不等式(数II)
対数, 対数関数, 対数方程式・不等式, 常用対数(数II)

後期(3Q, 4Q)

三角比の基礎(数I)
一般角, 弧度法(数II)
三角関数(sin, cos, tan)とその性質(数II)
三角関数のグラフ, 三角関数の方程式・不等式(数II)
加法定理とそれにより導出される公式, 三角関数の合成(数II)
三角比, 正弦・余弦定理(数I)
三角形の面積(数I)
点と直線(数II)
円の方程式(数II)
二次曲線(数C)
平面上の領域(数II)
個数の処理(数A)
二項定理(数II)
数え上げの法則, 順列と組み合わせ(数A)

順序に関しては高専ごとに異なりますが、1年で扱う内容は概ねこの通りであるはずです。
既に読者の方はお気づきかもしれませんが、ここで特筆すべき点は15・16歳の年齢のうちに数II、数III(一部数C)の内容をやるという点です。

高専では、2年以降から専門科目が本格化し、年次が上がると数学的な知識を要する専門科目が多くなります。

例として3年の電気系学科で習う電磁気学では微分・積分を使い、2・3年の情報系学科で習う情報数学(離散数学)では、計算機を扱うのに必要な数論、集合・論理を使います。

そのため、1年のうちから高校数学の範囲を普通校よりも早期に学ぶ、というわけです。(2年後期からは大学数学の範囲に入ります)

なお、1年生では上記の通り、数I/Aを超えた範囲を学習しますが、全てまでは学習しません。
残った範囲は2年生以降に学習します。(一部、そもそも学習せず飛ばす範囲もありますが、学科によっては専門科目の一部として学習する場合があります。)

高校で学ぶ数学との決定的な違い

上記より、高校と比べて高専の数学は進みが早い事はもうお分かりかと思いますが、それとは別にもう一つ決定的な違いがあります。

それは、大学入試対策を意識しないという点です。
多くの普通高校(特に進学校)では、大学等への進学をゴールとしているため、共通テストや各大学の入試問題を解く力を養うようにカリキュラムが組まれているかと思います。

しかし、高専はそれとは異なります。
先程も書いた通り、高専は工学を専門に学ぶ学校であるため、数学などは工学を学ぶために必要な基礎教養として学習します。
大学低学年で学ぶ基礎数学と同じような感じです。

そのため、高専の数学では、大学入試問題を解く力は養われません。
ただし、高年次になると大学編入・専攻科進学のための特別講座が用意されている学校もあります。
進学を考えている場合は、大学入試問題ではなく編入試験問題を解くのがおすすめです。

授業の難易度について

実際の授業については、授業をしっかり聞いていればついていけますが、やはり難しいと思う時もあります。何にせよ1年の頃から数II/IIIの範囲をやったりしますから。
特に対数や対数関数などで躓く学生が多い印象です。
躓かないようにするためにも、心がけるべき事を以下に挙げます。

1, 復習をしっかりしましょう

数学の授業は進みが早い分、当然ながら扱う内容の範囲は広いです。
そのため今まで学習した事があやふやになりがちです。
授業毎に、ノートをよく読み返したり、教科書の問題や問題集をコツコツ解くなどをして復習をしましょう。

2, 教員に積極的に質問をしましょう

これが一番大事かと思います。
数学科の教員はほとんどが修士・博士号を取得しており、正しく数学のプロです。
知識も豊富で分かりやすく説明をしてくださると思いますので、分からない箇所は積極的に質問をしてみましょう。
また、積極的に質問をすれば数学科教員と仲良くもなれます(実際に私も仲良くなりました)。

3, 友人や先輩を頼りましょう

高専に入学し、新しい友人や先輩と交流していく中で、数学が得意な学生は1人は必ずいるはずです。
分からない事は教えてもらい、逆に分からない子がいたら教えてあげましょう。
お互い助け合いながら授業を進めていくのもある意味では勉強だと思います。

4, 授業をしっかり聞きましょう

当たり前ではありますが、授業を聞かないと内容がそもそも理解できません。
授業を聞くことはテスト対策にも直結しますので、しっかり聞くようにしましょう。

定期試験の難易度と対策

定期試験は、授業をしっかり理解していれば解ける問題が基本として出題されますが、やはり難しい問題も出題されます。
試験対策で私がやるべきだと思うのは、教科書の章末問題・付属問題集・過去問です。

私が使用している教科書の章末問題は、その章で学んだ内容の総復習となっており、基本がしっかり身に着いたかの確認に便利です。

同時に使用している付属問題集(高専テキストシリーズ基礎数学問題集第2版)は、構成としては

A問題(基本的な知識技能の確認問題)
B問題(応用問題、中級的なため少し難易度が上がる)
C問題(難問、大学編入問題から出題される場合あり)

となっており、B問題まで解けば定期テスト対策としては十分です。余裕があればC問題もチャレンジしてみると良いと思います。
応用問題の解き方も問題集で身につくので、私は基本的にはこれを中心にテスト対策を進めていました。

過去問もかなり重要です。試験問題の出題傾向を掴めるので、1度は解くと良いと思います。ただし、過去問への過学習はお勧めしません。
出題傾向が掴めるとはいえ、過去問に過度に依存すると多様な問題に対応できなくなります。程々にしましょう。

また、チャート本などはやる必要はありません。教科書と問題集・配布資料で完結するので、それを中心に学習を進めましょう。

予習は必要か？

予習の必要性については、人によって意見が分かれますが、私は不要と考えています。
授業をしっかり聞き、分からない点は質問をし、授業内で例題を解けばしっかり理解できましたし、それで十分だと思っています。
強いて言うなら、授業前に教科書を軽く読んだり、まだ習っていないページを読み物として読んでみるのがおすすめです。
(※ただし、教員から予習の指示があった場合はそれに従いましょう。学習上意味があるはずです)

入学前の春休み中にやっておいた方がいい事

入学前に、数学科から入学前課題が出される場合が多いので、それをまずはやりましょう。中学数学の知識で十分理解できるはずです。
その課題で解けない問題があったとき、大抵は中学数学で欠けている知識がある場合が多いかと思います。
解説などを読み、関連している中学範囲を復習しましょう。

また、私個人としては、

二次方程式の解の公式の導出
三平方の定理の証明

の2つできるようにしておいたら得かと思います。

解の公式が導出できるようになれば、解がなぜ2つあるのか理解が深まりますし、実際の授業で扱う二次方程式・2次関数で本質が捉えやすくなります。
また、導出の過程で「平方完成」と呼ばれる手法を用いますが、これは2次関数の分野でとても重要になってきます。

三平方の定理の証明についても、これができるようになると幾何学への理解が深まり、後に学ぶ三角関数や、平面上の図形で何かしらヒントになるかなと思います。

以下、この2つのやり方を示します。

二次方程式の解の公式の導出

$$ax^2+bx+c=0$$の両辺を$a$で割り, $\frac{c}{a}$を移項し,
$$x^2+ \frac{b}{a}x = -\frac{c}{a} $$
両辺に$(\frac{b}{2a})^2$を足して(平方完成その1),
$$x^2+ \frac{b}{a}x+(\frac{b}{2a})^2 = -\frac{c}{a} + (\frac{b}{2a})^2 $$
左辺を$(a+b)^2$の形にし, 右辺の()を展開して(平方完成その2),
$$(x + \frac{b}{2a})^2 = -\frac{c}{a} + \frac{b^2}{4a^2} $$
$$(x + \frac{b}{2a})^2 = \frac{b^2-4ac}{4a^2} $$
左辺について解き,
$$x + \frac{b}{2a} = \frac{±\sqrt{b^2-4ac}}{2a} $$
$$x = \frac{-b±\sqrt{b^2-4ac}}{2a} $$
以上で, 解の公式が導出された.

三平方の定理の証明(アインシュタインの方式)

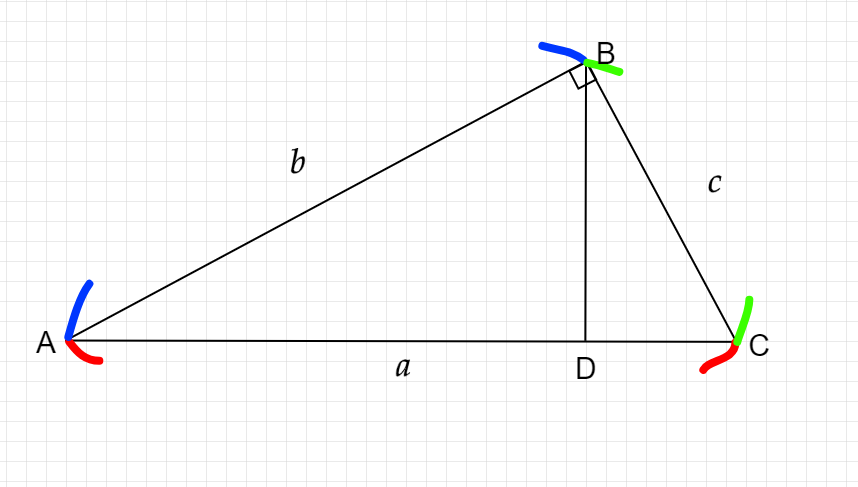直角三角形の証明図

$⊿ABC$に, 直角$B$から辺$AC$へ垂線を引き, その接点を点$D$と定める. すると,
$$⊿ABC\sim⊿ADB\sim⊿BDC$$
の関係にある, 3つの相似な三角形ができる.
これらの相似比は, それぞれの斜辺の長さを$a, b, c$とすると,
$$⊿ABC:⊿ADB:⊿BDC = a:b:c$$
となる.
同時に面積比も,
$$⊿ABC:⊿ADB:⊿BDC = a^2:b^2:c^2$$
が成り立つ.
それに伴い, それぞれの三角形の面積は, 定数$k$を用いて,
\begin{align} ⊿ABC = a^2k\\ ⊿ADB = b^2k\\ ⊿BDC = c^2k \end{align}
と表せる.
上記の図より, $⊿ABC = ⊿ADB + ⊿BDC$なので,
$$a^2k = b^2k + c^2k$$
この式の両辺を$k$で割って,
$$a^2 = b^2 + c^2$$
以上で, 三平方の定理が証明された.