昼の長さを求める
1日の間に日が出ている時間（$:=$ 昼の長さ）を計算してみました．秋分からの日数と緯度を変数として太陽が当たる時間を計算します．
設定
地球は球体であり，一定の角速度で自転しながら一定の角速度で円上を公転すると仮定する．また公転周期を1年，自転周期を1日とする．1年は365日とし閏年などは考えないとする．
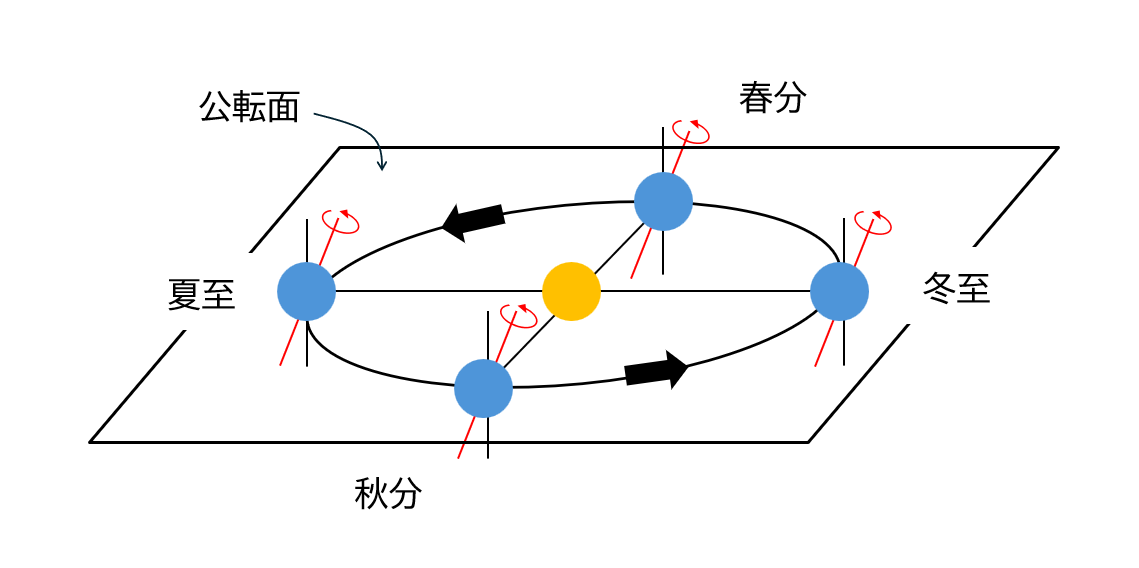公転
次のようにパラメタを設定する．
(1)公転面上の位置
$D\in\R$：秋分からの日数(日)
$\dps\psi:=\frac{D}{365}\times2\pi$：秋分から$D$日後までに地球が進んだ角度(rad)
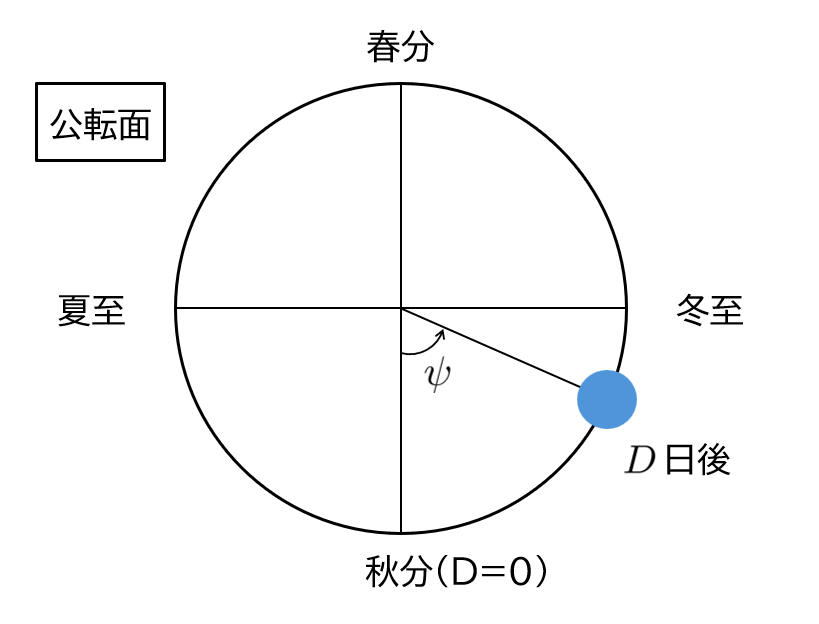公転面
(2)地軸の傾き
- $\dps\phi_0:=23.4\times\frac{\pi}{180}$：地軸の傾き(rad)
- $\phi(\psi)$：太陽から地球を見たときの見かけの地軸の傾き(rad)
とすると，
$$\tan{\phi(\psi)}=\sin{\psi}\tan{\phi_0} $$と計算される．特に$$\ \phi(0)=0,\ \ \phi\left(\frac{\pi}{2}\right)=\phi_0$$
(3)地球上の位置（考える地点の緯度）
- $L\in(-90,90)$：緯度(°)
- $\dps\theta=L\times\frac{\pi}{180}\in\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$：緯度(rad)
とする．
導出
次の図は地軸方向から秋分過ぎ頃の地球を見た図であり，影の部分が地上の夜を表す．
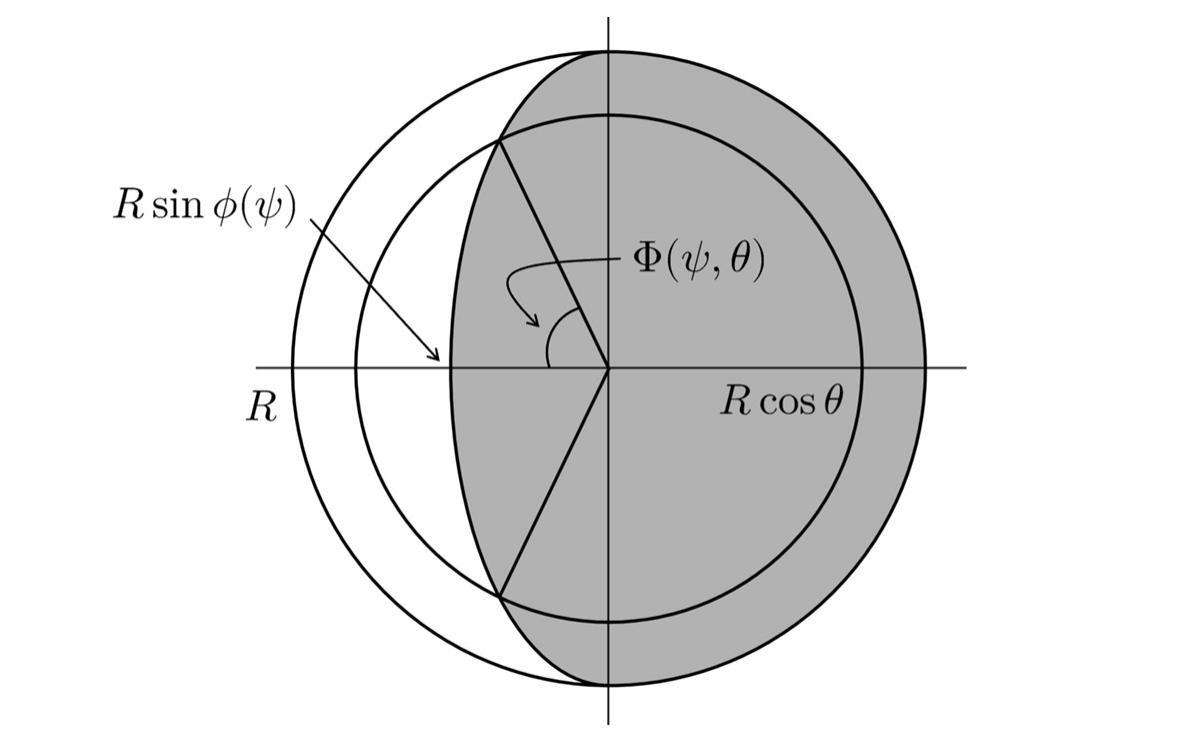地軸方向から秋分過ぎ頃の地球を見た図
地球の半径を$R$とおくと，緯度$L°=θ[\rm{rad}]$の点は半径$R\cos{\theta}$の円軌道を描く．影の境界のうち左側（太陽側）は長径$R$，短径$R\sin{\phi(\psi)}$の楕円である．$\Phi(\psi,\theta)$を図のように置くと，
\begin{align} \Phi(\psi,\theta)=\cos^{-1}{(\tan{\phi(\psi)}\tan{\theta})} \end{align}
但し，$\dps-\frac{\pi}{2}+\phi_0<\theta<\frac{\pi}{2}-\phi_0$とする．（この範囲でないと昼夜が入れ替わらない．）
以下この式を導出する．
点の軌道と影の境界の交点を２通りで表すと，
$$(R\cos{\theta}\cos{\Phi(\psi,\theta)},R\cos{\theta}\sin{\Phi(\psi,\theta)})=(R\sin{\phi(\psi)}\cos{\Psi},R\sin{\Psi})$$
それぞれ$R$で割ってノルムの2乗をとると，
\begin{align}
\cos^2{\theta}
&=\sin^2{\phi(\psi)}\cos^2{\Psi}+\sin^2{\Psi}\\
&=\sin^2{\phi(\psi)}\cos^2{\Psi}+(1-\cos^2{\Psi})\\
&=1-\cos^2{\Psi}(1-\sin^2{\phi(\psi)})\\
&=1-\cos^2{\Psi}\cos^2{\phi(\psi)}
\end{align}
よって
\begin{align}
\cos^2{\Psi}
=\frac{1-\cos^2{\theta}}{\cos^2{\phi(\psi)}}=\frac{\sin^2{\theta}}{\cos^2{\phi(\psi)}}
\end{align}
従って$\dps\cos{\Psi}=\frac{\sin{\theta}}{\cos{\phi(\psi)}}$と，第１成分の$\cos{\theta}\cos{\Phi(\psi,\theta)}
=\sin{\phi(\psi)}\cos{\Psi}$から，
\begin{align}
\cos{\Phi(\psi,\theta)}
&=\frac{\sin{\phi(\psi)}\cos{\Psi}}{\cos{\theta}}\\
&=\frac{\sin{\phi(\psi)}}{\cos{\theta}}\frac{\sin{\theta}}{\cos{\phi(\psi)}}\\
&=\tan{\phi(\psi)}\tan{\theta}\
\Phi(\psi,\theta)\\
&=\cos^{-1}{(\tan{\phi(\psi)}\tan{\theta})}
\end{align}
結論
以上より，昼の長さ$T(\psi,\theta)$は，
\begin{align} T(\psi,\theta) &=\frac{365}{360}\cdot\frac{24}{2\pi}\cdot2\Phi(\psi,\theta)\\ &=\frac{365}{360}\cdot\frac{24}{\pi}\cos^{-1}{(\tan{\phi(\psi)}\tan{\theta})}\\ &=\frac{365}{360}\cdot\frac{24}{\pi}\cos^{-1}{(\sin{\psi}\tan{\phi_0}\tan{\theta})}\\ &=\frac{365}{360}\cdot\frac{24}{\pi}\cos^{-1}{\left(\tan{\left(23.4\times\frac{\pi}{180}\right)}\tan{\left(\frac{\pi L}{180}\right)}\sin{\left(\frac{2\pi D}{365}\right)}\right)} \end{align}
$$T(\psi,\theta) =\frac{365}{360}\cdot\frac{24}{\pi}\cos^{-1}{\left(\tan{\left(23.4\times\frac{\pi}{180}\right)}\tan{\left(\frac{\pi L}{180}\right)}\sin{\left(\frac{2\pi D}{365}\right)}\right)}$$
実際に代入
見やすさのため$\dps\frac{365}{360}$倍を除いた．
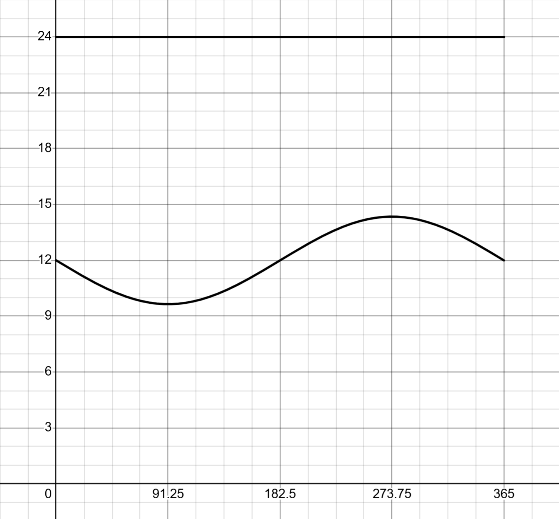
冬至と夏至が観察できる．
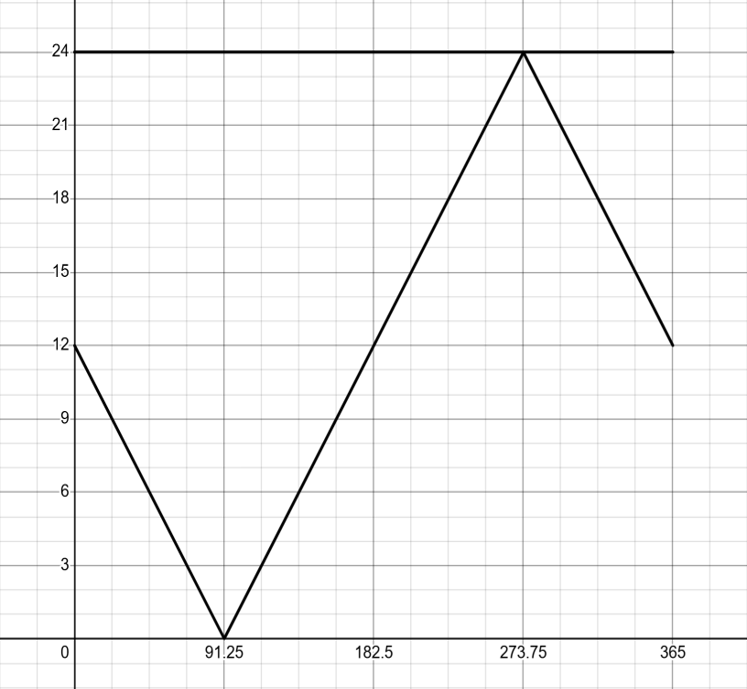
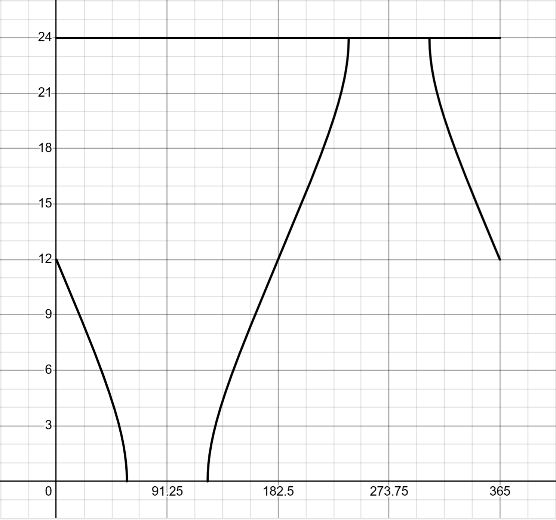
冬至付近は極夜，夏至付近は白夜となっている．
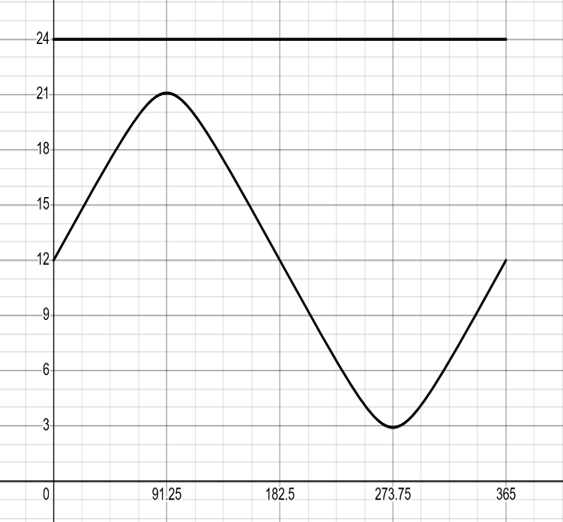
北半球と増減が逆転する．
実際計算した日の京都の昼の長さを計算した結果，5分程度のズレしか起こっておらず，思っていたより誤差を小さくできていたようである．
