文献あり

【20/38】韓国の共テ模試を解いてみよう【2025学年度６月】

230

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

どうも！　ITetsuYKです。はじめまして、またはお久しぶりです。
私は韓国に住んでいる一般大学生なんですが、ゆえに韓国の共テに割と興味があるんですよね。すでに受けている身でもありますが。

てなわけで、今年の６月模試を解いてみようではないかと。思ったわけでございます。解きます。はい。

韓国の共テは1～22番の『数学Ⅰ』・『数学Ⅱ』から出題される共通問題と、23～30番の選択問題があります。文系は大体『確立と統計』の問題を、理系は大体『微積分』の問題を解きます。『幾何』という科目もありますが（日本の数B後半に相当）……。まぁほぼ選ばないです。

この文書では『幾何』から出題される問題を除く全問題を私YKが解いていきます。選択科目では『確立と統計』をPS、『微積分』をCCとナンバリングしています。解説用として書いているので、ちょっと文章が固いときがあるかも。

まぁ御託は置いておいて、早速やっていきましょう。本来「？」で終わる問題は選択式ですが、めんどくさいので全部叙述型にしてあります。

ちなみにまだ全然途中ですがモチベの関係上とりあえず一回上げておきます。

1. 数学Ⅰ：指数と対数（２点）

${(\frac{5}{\sqrt[3]{25}})}^{\frac{3}{2}}$ の値は？

$\begin{aligned} {(\frac{5}{\sqrt[3]{25}})}^{\frac{3}{2}} = {(\frac{5}{25^{\frac{1}{3}}})}^{\frac{3}{2}} & = (5 \times 25^{- \frac{1}{3}})^{\frac{3}{2}} = {5 \times (5^{2})^{- \frac{1}{3}}}^{\frac{3}{2}} \\ = (5 \times 5^{- \frac{2}{3}})^{\frac{3}{2}} = (5^{\frac{1}{3}})^{\frac{3}{2}} = 5^{\frac{1}{2}} = \sqrt{5} . ◼ \end{aligned}$

2. 数学Ⅱ：微分係数／多項関数の微分法（２点）

関数 $f (x) = x^{2} + x + 2$ に対し $lim_{h \to 0} \frac{f (2 + h) - f (2)}{h}$ の値は？

(i：愚直に代入して解く)
$\begin{aligned} lim_{h \to 0} \frac{f (2 + h) - f (2)}{h} & = lim_{h \to 0} \frac{{(2 + h)^{2} + (2 + h) + 2} - {2^{2} + 2 + 2}}{h} \\ = lim_{h \to 0} \frac{h^{2} + 5 h}{h} = lim_{h \to 0} (h + 5) = 5 . ◼ \end{aligned}$

(ii：微分したのち代入する）
$f^{'} (x) = 2 x + 1 (+ 0)$ なので
$lim_{h \to 0} \frac{f (2 + h) - f (2)}{h} = f^{'} (2) = 2 \times 2 + 1 = 5 . ◼$

3. 数学Ⅰ：級数（３点）

数列 ${a_{n}}$ に対して $\sum_{k = 1}^{5} (a_{k} + 1) = 9$ であり $a_{6} = 4$ であるとき、 $\sum_{k = 1}^{6} a_{k}$ の値は？

$\sum_{k = 1}^{5} (a_{k} + 1) = \sum_{k = 1}^{5} a_{k} + \sum_{k = 1}^{5} + 1 = \sum_{k = 1}^{5} a_{k} + 5 = 9$ であるため $\sum_{k = 1}^{5} a_{k} = 9 - 5 = 4$ である。なので
$\sum_{k = 1}^{6} a_{k} = \sum_{k = 1}^{5} a_{k} + a_{6} = 4 + 4 = 8 . ◼$

4. 数学Ⅱ：関数の極限（３点）

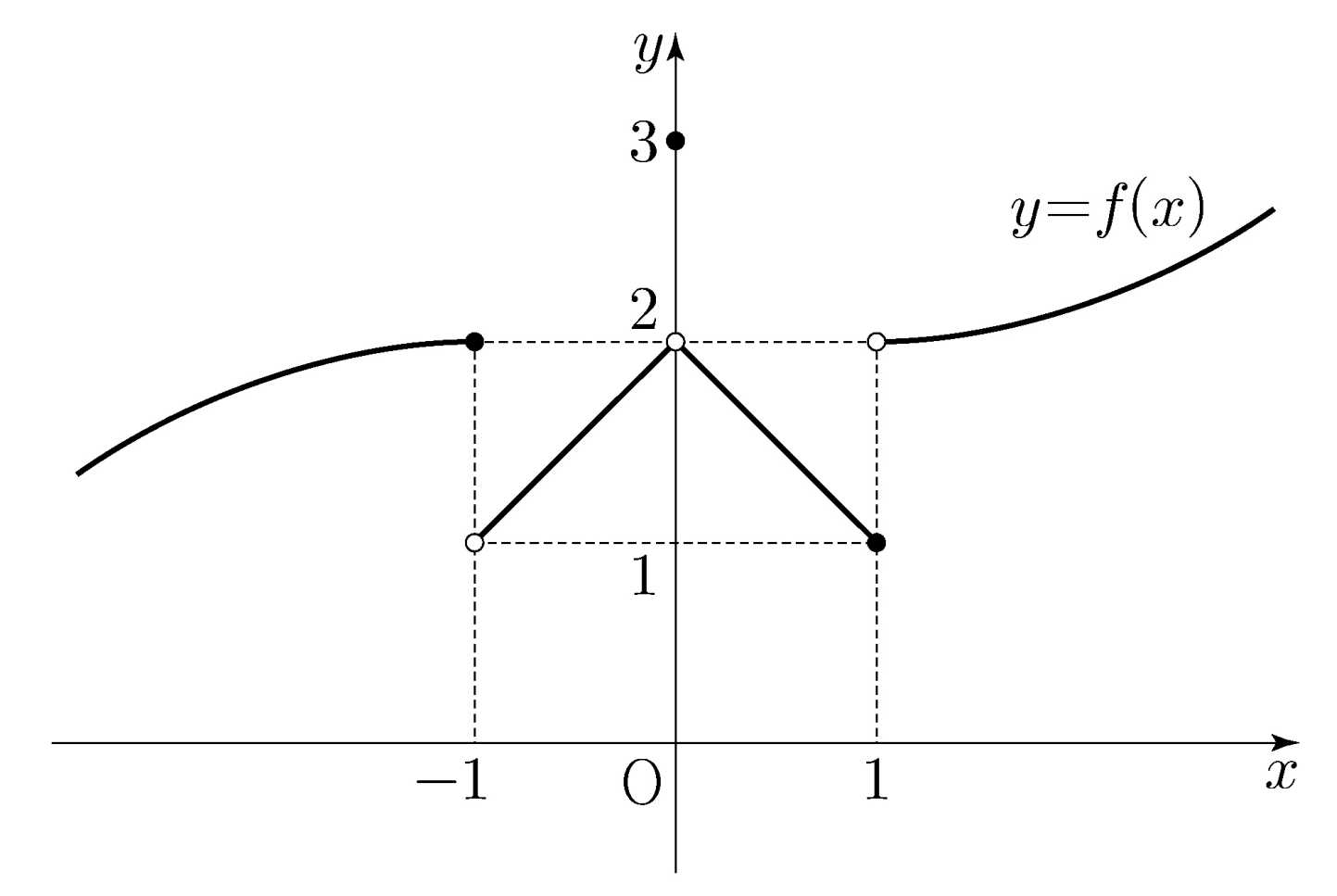
関数 $y = f (x)$ のグラフが以下の図に描かれている。
４番
$lim_{x \to 0 +} f (x) + lim_{x \to 1 -} f (x)$ の値は？

〈記号〉
$a$ への関数 $f$ の左側極限が $L_{1}$ 、右側極限が $L_{2}$ であることをそれぞれ $lim_{x \to a -} f (x) = L_{1}$ 、 $lim_{x \to a +} f (x) = L_{2}$ と表す。

$lim_{x \to 0 +} f (x) + lim_{x \to 1 -} f (x) = 2 + 1 = 3 . ◼$

5. 数学Ⅱ：多項関数の微分法（３点）

関数 $f (x) = (x^{2} - 1) (x^{2} + 2 x + 2)$ に対して $f^{'} (1)$ の値は？

展開するより積の微分法を使ったほうがマシ。
$\begin{aligned} f^{'} (x) & = {(x^{2} - 1)^{'}} (x^{2} + 2 x + 2) + (x^{2} - 1) {(x^{2} + 2 x + 2)^{'}} \\ = 2 x (x^{2} + 2 x + 2) + (x^{2} - 1) (2 x + 2) \end{aligned}$
なので $f^{'} (1) = 2 (1 + 2 + 2) + (1 - 1) (2 + 2) = 10 . ◼$

6. 数学Ⅰ：三角関数（３点）

$π < θ < \frac{3}{2} π$ である $θ$ に対して $\sin (θ - \frac{π}{2}) = \frac{3}{5}$ であるとき、 $\sin θ$ の値は？

$y = \sin x$ と $y = \cos x$ のグラフから全ての実数 $α$ に対して $\sin (α - \frac{π}{2}) = - \cos α$ と分かるので、 $\sin (θ - \frac{π}{2}) = - \cos θ = \frac{3}{5}$ 、また $π < θ < \frac{3}{2} π$ より $\sin θ < 0$ なので
$\sin θ = - \sqrt{1 - \cos^{2} θ} = - \sqrt{1 - \frac{9}{25}} = - \frac{4}{5} . ◼$

7. 数学Ⅱ：導関数の応用（３点）

$x$ に対する方程式 $x^{3} - 3 x^{2} - 9 x + k = 0$ の互いに違う実数解の個数が $2$ になるようにする全ての実数 $k$ の値の和は？

互い次違う実数解の個数が2ということは１個の解が重解ということ。なら一つの実数 $α$ で $f (α) = f^{'} (α) = 0$ が成立しなければならない。

$f^{'} (x) = 3 x^{2} - 6 x - 9 = 3 (x - 3) (x + 1)$
なので $f^{'} (x)$ は $x = 3$ または $x = - 1$ であるとき $0$ 。

(i) $α = 3$
$f (3) = 27 - 3 \times 3^{2} - 9 \times 3 + k = k - 27 = 0, k = 27.$

(ii) $α = - 1$
$f (- 1) = - 1 - 3 \times 1 - 9 \times (- 1) + k = k + 5 = 0, k = - 5.$

ゆえに答えは $27 + (- 5) = 22 . ◼$

8. 数学Ⅰ：等比数列：３点

$a_{1} a_{2} < 0$ である等比数列 ${a_{n}}$ に対して
$a_{6} = 16, 2 a_{8} - 3 a_{7} = 32$
であるとき、 $a_{9} + a_{11}$ の値は？

初項を $a$ 、公比を $r$ とする。なら
${\begin{cases} a r^{5} = 16 & \dots \dots (1) \\ 2 a r^{7} - 3 a r^{6} = a r^{6} (2 r - 3) = 32 & \dots \dots (2) \end{cases}$
という連立方程式を立てることができ、(2)に(1)を代入すると
$16 r (2 r - 3) = 32, 2 r^{2} - 3 r + 2 = (2 r + 1) (r - 2) = 0, r = - \frac{1}{2} または r = 2$
となるが、 $a_{1} a_{2} = a^{2} r < 0$ から $r < 0$ なので $r = - \frac{1}{2}$ である。

これを(1)に代入すると $a r^{5} = a \times {(- \frac{1}{2})}^{5} = - \frac{a}{32} = 16, a = - 2^{9}$ となる。

なので
$\begin{aligned} a_{9} + a_{11} & = a r^{8} + a r^{10} \\ = a r^{8} (1 + r^{2}) \\ = (- 2)^{9} \times {(- \frac{1}{2})}^{8} \times {1 + {(- \frac{1}{2})}^{2}} \\ = - 2 \times \frac{5}{4} = - \frac{3}{2} . ◼ \end{aligned}$

9. 数学Ⅱ：関数の連続（３点）

関数
$f (x) = {\begin{cases} x - \frac{1}{2} & (x < 0) \\ - x^{2} + 3 & (x \geq 0) \end{cases}$
に対し、関数 ${f (x) + a}^{2}$ が実数全体の集合で連続であるとき、定数 $a$ の値は？

〈記号〉
$A$ が $B$ より等しいか大きいことを $A \geq B$ と表す。等しいか小さいことも同様、 $A \leq B$ と表す。

$\begin{aligned} lim_{x \to 0 -} {f (x) + a}^{2} = lim_{x \to 0 -} {(x + a - \frac{1}{2})}^{2} = {(a - \frac{1}{2})}^{2}, \\ lim_{x \to 0 +} {f (x) + a}^{2} = lim_{x \to 0 +} (a + 3 - x^{2})^{2} = (a + 3)^{2} \end{aligned}$
なので ${f (x) + a}^{2}$ が実数全体で（特に $x = 0$ で）連続になるようには ${(a - \frac{1}{2})}^{2} = (a + 3)^{2}$ である必要がある。

実数 $A, B, C$ に対し $| A - B |$ は $A$ と $B$ の間の距離を意味し、 $A$ と $B$ の間の距離、そして $B$ と $C$ の間の距離が同じなら $B$ は線分 $A C$ の中点なので

$\begin{aligned} {(a - \frac{1}{2})}^{2} = (a + 3)^{2} & ⟺ | a - \frac{1}{2} | = | a + 3 | \\ ⟺ a = \frac{1}{2} \times (\frac{1}{2} - 3) = - \frac{5}{4} . ◼ \end{aligned}$

10. 数学Ⅰ：三角関数の応用（４点）

次の条件を満たす三角形 $A B C$ の外接円の面積が $9 π$ であるとき、三角形 $A B C$ の面積は？

(ア) $3 \sin A = 2 \sin B$
(イ) $\cos B = \cos C$

外接円の面積が $9 π$ なら、その半径は $3$ となる。

角 $A, B, C$ の対応辺をそれぞれ $a, b, c$ とすれば正弦法則により $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 6$ が成立する。

$\cos B = \cos C$ なら $B = C$ なので（ $\cos x$ は区間 $(0, π)$ で一対一対応であるため） $b = c$ となり、これの値を $d$ とする。また、 $B = C$ の値を $θ$ とする。

であるならば、以下の等式が成立する。
$\frac{a}{\sin A} = \frac{d}{\sin θ} = 6, \sin θ = \frac{d}{6}$

また、 $3 \sin A = 2 \sin θ$ より $\sin A = \frac{2}{3} \sin θ$ であるため、上記の等式を次のように書くことができる。
$\frac{a}{(2 / 3) \sin θ} = \frac{d}{\sin θ} = 6 ⟹ \frac{3}{2} a = d = 6 \sin θ$

$B = C$ から $B$ と $C$ ともに $π / 2$ 以下、つまり $\cos B$ 、 $\cos C$ の両方の値が $0$ 以上であることは明白であるため、 $\cos θ = \sqrt{1 - \frac{d^{2}}{36}}$ となり、 $a = \frac{2}{3} d$ であるため余弦法則により
$\begin{aligned} \cos^{2} θ & = 1 - \frac{d^{2}}{36} = {(\frac{a^{2} + b^{2} - c^{2}}{2 a b})}^{2} = {[\frac{{(2 / 3) d}^{2} + d^{2} - d^{2}}{2 {(2 / 3) d} d}]}^{2} = \frac{1}{9} \\ ⟹ \frac{d^{2}}{36} = \frac{8}{9} \\ ⟹ d = 4 \sqrt{2}, a = \frac{8}{3} \sqrt{2}, \sin θ = \frac{2}{3} \sqrt{2} \end{aligned}$
となる。なので
$△ A B C = \frac{1}{2} a b \sin C = \frac{1}{2} a d \sin θ = \frac{1}{2} \times \frac{8}{3} \sqrt{2} \times 4 \sqrt{2} \times \frac{2}{3} \sqrt{2} = \frac{32}{9} \sqrt{2} . ◼$

11. 数学Ⅱ：微分係数（４点）

最高次項の係数が1であり $f (0) = 0$ である三次関数 $f (x)$ が
$lim_{x \to a} \frac{f (x) - 1}{x - a} = 3$
を満たす。曲線 $y = f (x)$ の上の点 $(a, f (a))$ での接線の $y$ 切片が $4$ であるとき、 $f (1)$ の値は？
（ただし、 $a$ は定数である。）

$lim_{x \to a} \frac{f (x) - 1}{x - a} = 3$ であることはこの極限が $\frac{0}{0}$ 不定形を持つことを意味するため、 $f (a) - 1$ の値が $0$ となると言える。なので $f (a) = 1$ 。また、これより
$lim_{x \to a} \frac{f (x) - 1}{x - a} = lim_{x \to a} \frac{f (x) - f (a)}{x - a} = f^{'} (a) = 3$
であることが分かる。なので点 $(a, f (a))$ で引いた曲線 $y = f (x)$ の接線 $l$ は以下のような方程式で表すことができる。
$l : y = 3 (x - a) + 1$

ここで曲線 $l$ の $y$ 切片が $4$ なら $l$ に $x = 0, y = 4$ を代入しても等式が成立しなければならないので
$4 = 3 (0 - a) + 1 = 1 - 3 a, a = - 1.$

関数 $f (x)$ を $f (x) = x^{3} + b x^{2} + c x + d$ とすれば $f (0) = d = 0$ であり、 $f^{'} (x) = 3 x^{2} + 2 b x + c$ であるため $f (- 1) = 1, f^{'} (- 1) = 3$ から
$\begin{aligned} {\begin{cases} (- 1)^{3} + b (- 1)^{2} + c (- 1) = b - c - 1 = 1 \\ 3 (- 1)^{2} + 2 b (- 1) + c = c - 2 b + 3 = 3 \end{cases} \\ ⟹ & {\begin{cases} b - c = 2 \\ c = 2 b \end{cases} \\ ⟹ & b - 2 b = - b = 2 \\ ⟹ & {\begin{cases} b = - 2 \\ c = - 4 \end{cases} \end{aligned}$
であることがわかる。なので $f (x) = x^{3} - 2 x^{2} - 4 x$ であり、 $f (1) = - 5 . ◼$

12. 数学Ⅰ：指数関数・対数関数（４点）

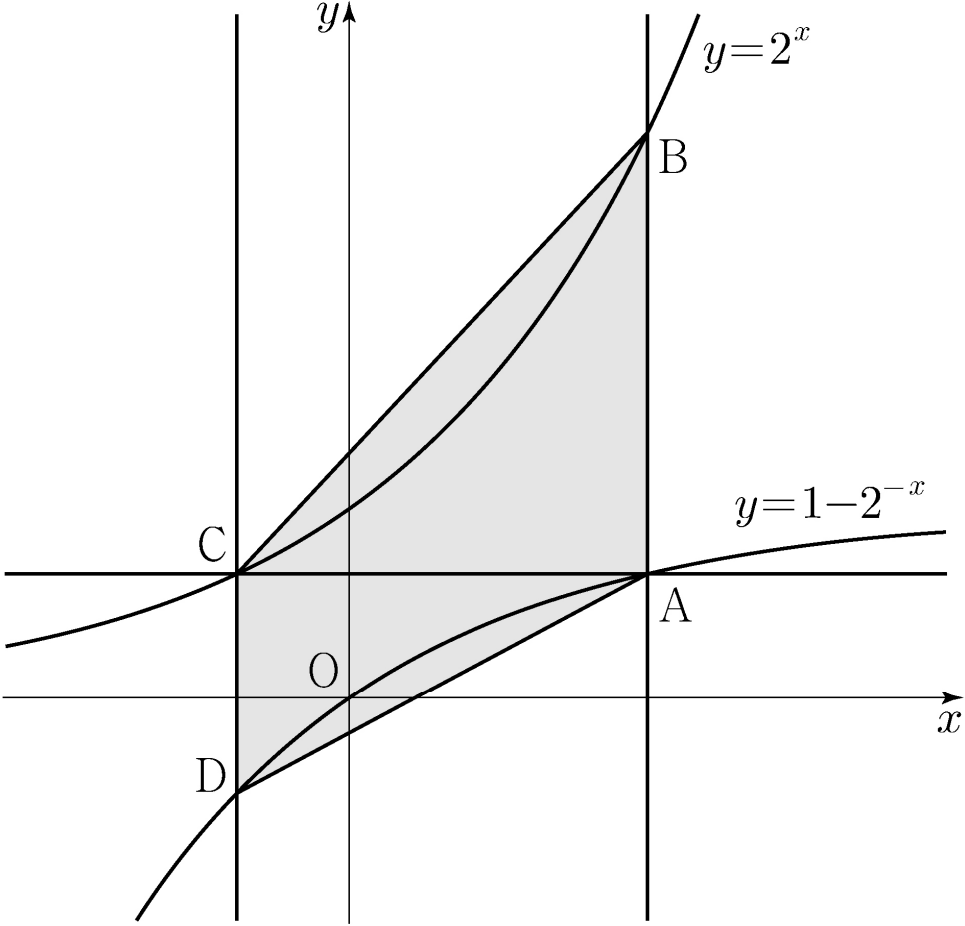
下の図のように曲線 $y = 1 - 2^{- x}$ の上の第 $1$ 象限にある点 $A$ を通り $y$ 軸に平行である直線が曲線 $y = 2^{x}$ と交わる点を $B$ とする。点 $A$ を通り $x$ 軸に平行である直線が曲線 $y = 2^{x}$ と交わる点を $C$ 、点 $C$ を通り $y$ 軸に平行である直線が曲線 $y = 1 - 2^{- x}$ と交わる点を $D$ とする。 $\overset{―}{A B} = 2 \overset{―}{C D}$ であるとき、四角形 $A B C D$ の面積は？
12番 12番

〈記号〉
線分 $A B$ を $\overset{―}{A B}$ と表す。

便宜上、任意の点 $R$ の $x$ 座標、 $y$ 座標をそれぞれ $x (R), y (R)$ とする。公式的な記号ではないので注意。

点 $D$ から $A$ までの $x$ の変化率、 $y$ の変化率をそれぞれ $Δ x_{1}, Δ y_{1}$ とし、点 $C$ から $B$ までの $x$ の変化率、 $y$ の変化率をそれぞれ $Δ x_{2}, Δ y_{1}$ とする。なら $Δ x_{1} = Δ x_{2}$ 、そして $Δ y_{2} = 2 Δ y_{1}$ が成立する。

$x (C) = x (D)$ の値を $a$ 、 $x (A) = x (B)$ の値を $b$ とする。なら $y (A) = y (C)$ と $Δ y_{2} = 2 Δ y_{1}$ から
$\begin{aligned} {\begin{cases} 2^{a} = 1 - 2^{- b} \\ 2^{b} - 2^{a} = 2 {(1 - 2^{- b}) - (1 - 2^{- a})} = 2^{1 - a} - 2^{1 - b} \end{cases} ⟹ {\begin{cases} 2^{a} = 1 - 2^{- b} \\ 2^{b} (1 + 2^{1 - 2 b}) - 2^{a} (1 + 2^{1 - 2 a}) = 0 \end{cases} \\ ⟹ & 2^{b} (1 + 2^{1 - 2 b}) - (1 - 2^{- b}) {1 + \frac{2}{(1 - 2^{- b})^{2}}} = 0 \end{aligned}$

$2^{- b}$ を $B$ とする。なら $B > 0$ であり、 $2^{a} = 1 - 1 = 0$ を満たす実数 $a$ は存在しないので $B \neq 1$ である。
$\begin{aligned} \frac{1}{B} (1 + 2 B^{2}) - (1 - B) {1 + \frac{2}{(1 - B)^{2}}} & = \frac{1 + 2 B^{2}}{B} - \frac{(1 - B)^{2} + 2}{1 - B} \\ = \frac{(1 - B) (1 + 2 B^{2}) - B (B^{2} - 2 B + 3)}{B (1 - B)} \\ = \frac{1 - B + 2 B^{2} - 2 B^{3} - B^{3} + 2 B^{2} - 3 B}{B (1 - B)} \\ = \frac{- 3 B^{3} + 4 B^{2} - 4 B + 1}{B (1 - B)} = 0 \end{aligned}$
となる。これの式を $\frac{P (B)}{Q (B)} = 0$ として、 $P (B)$ のみを考慮すると $P (\frac{1}{3}) = - \frac{3}{27} + \frac{4}{9} - \frac{4}{3} + 1 = 0$ なので $P (B)$ は $(3 B - 1)$ を因数として持つ。これを因数分解すると（過程は省略、組立所法を利用） $P (B) = - (3 B - 1) (B^{2} - B + 1)$ なので $P (B) = 0$ の解は $B = \frac{1}{3}$ となる。 $(B^{2} - B + 1) = 0$ は判別式 $D$ が $1 - 4 < 0$ であるため実数解はない。

$B = 2^{- b} = 1 / 3 = 3^{- 1}$ なので $b = \log_{2} 3$ である。 $2^{a} = 1 - 2^{- b}$ から $2^{a} = 1 - \frac{1}{3} = \frac{2}{3}, a = 1 - \log_{2} 3$ 。

$◻ A B C D$ は台形であるため、 $\overset{―}{A B}, \overset{―}{C D}, \overset{―}{A C}$ の長さで $◻ A B C D$ の面積を求めることができる。
$\overset{―}{A C} = b - a = 2 \log_{2} 3 - 1, \overset{―}{C D} = 2^{b} - 2^{a} = 3 - \frac{2}{3} = \frac{7}{3}, \overset{―}{A B} = \frac{1}{2} \overset{―}{C D} = \frac{7}{6}$
なので
$◻ A B C D = \frac{1}{2} \times (\overset{―}{A B} + \overset{―}{C D}) \times \overset{―}{A C} = \frac{1}{2} \times \frac{7}{2} \times (2 \log_{2} 3 - 1) = \frac{7}{2} {l o g}_{2} 3 - \frac{7}{4} . ◼$

13. 積分の応用（４点）

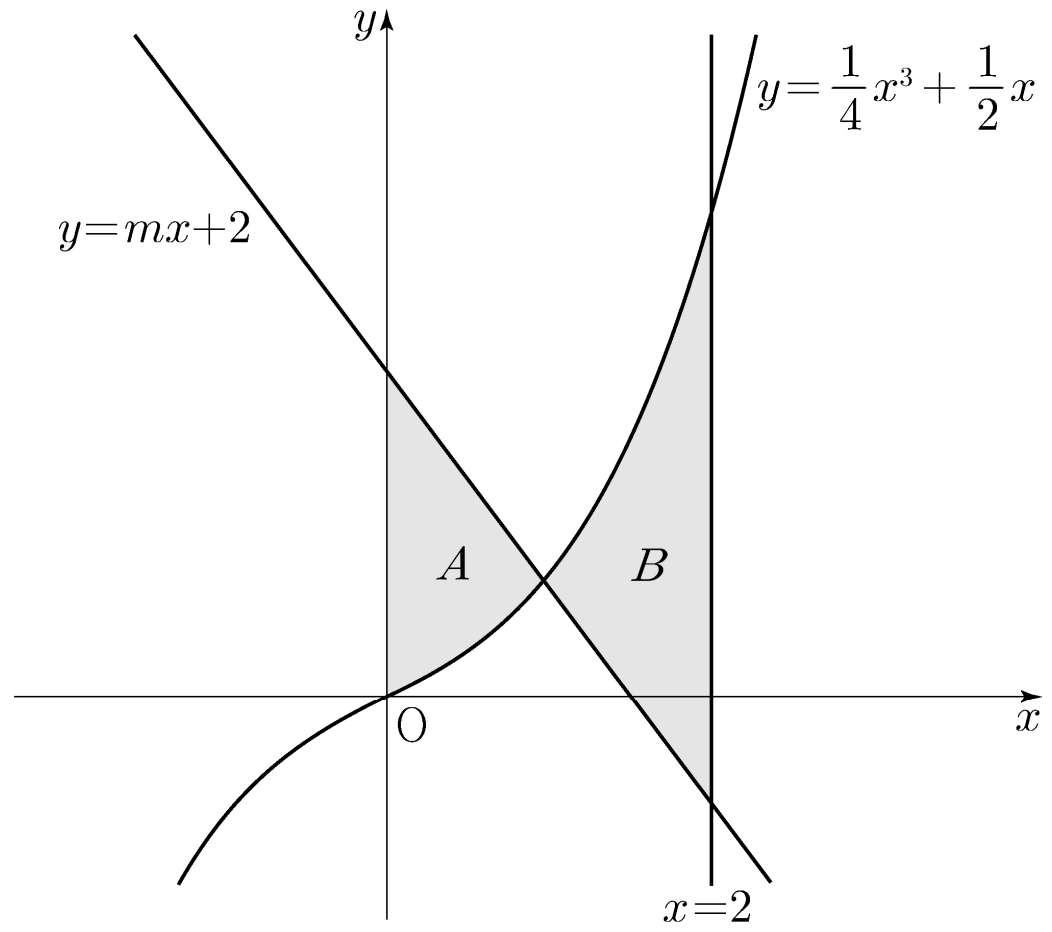
曲線 $y = \frac{1}{4} x^{3} + \frac{1}{2} x$ と直線 $y = m x + 2$ 、および $y$ 軸に囲まれた領域の面積を $A$ 、曲線 $y = \frac{1}{4} x^{3} + \frac{1}{2} x$ と二つの直線 $y = m x + 2$ 、 $x = 2$ で囲まれた領域の面積を $B$ とする。 $B - A = \frac{2}{3}$ であるとき、定数 $m$ の値は？（ただし、 $m < - 1$ である。）
13番 13番

関数 $f, g$ を $f (x) = \frac{1}{4} x^{3} + \frac{1}{2} x, g (x) = m x + 2$ とする。また、 $x$ に対する方程式 $f (x) = g (x)$ の解を $α$ とする。 $f$ は常に増加、 $g$ は常に減少関数であるため $α$ は唯一の実数として存在する。

$A = \int_{0}^{α} {g (x) - f (x)} d x, B = \int_{α}^{2} {f (x) - g (x)} d x$
であるため、
$\begin{aligned} B - A & = \int_{α}^{2} {f (x) - g (x)} d x - \int_{0}^{α} {g (x) - f (x)} d x \\ = \int_{α}^{2} {f (x) - g (x)} d x + \int_{0}^{α} {f (x) - g (x)} d x \\ = \int_{0}^{2} {f (x) - g (x)} d x \dots \dots (1) \end{aligned}$
と言える。

(1)が $B - A = \frac{2}{3}$ と同値であることを用いると
$\begin{aligned} \int_{0}^{2} {f (x) - g (x)} d x & = \int_{0}^{2} {(\frac{1}{4} x^{3} + \frac{1}{2} x) - (m x + 2)} d x \\ = \int_{0}^{2} {\frac{1}{4} x^{3} - (m - \frac{1}{2}) x - 2} d x \\ = [\frac{x^{4}}{16} - \frac{1}{4} (2 m - 1) x^{2} - 2 x]_{0}^{2} \\ = 1 - (2 m - 1) - 4 = - 2 m + 3 = \frac{2}{3}, m = - \frac{7}{6} . ◼ \end{aligned}$

14. 数学Ⅰ：対数関数（４点）

次の条件を満たすすべての自然数 $k$ の値の和は？

$\log_{2} \sqrt{- n^{2} + 10 n + 75} - \log_{4} (75 - k n)$ の値が正の数になるようにする自然数 $n$ の個数が $12$ である。

対数関数・無理関数の定義域による $n$ の範囲を考える。 $n$ は自然数であるため、 $n > 0$ を基本前提として考える。
${\begin{cases} - n^{2} + 10 n + 75 = - (n + 5) (n - 15) > 0 \\ 75 - k n > 0 \end{cases} ⟹ {\begin{cases} 0 < n < 15 & \dots \dots (1) \\ n < \frac{75}{k} & \dots \dots (2) \end{cases}$

$\begin{aligned} \log_{2} \sqrt{- n^{2} + 10 n + 75} - \log_{4} (75 - k n) > 0 \\ ⟹ & \frac{1}{2} \log_{2} (- n^{2} + 10 n + 75) > \frac{1}{2} \log_{2} (75 - k n) \\ ⟹ & - n^{2} + 10 n + 75 > 75 - k n \\ ⟹ & n^{2} - (k + 10) n < 0 ⟹ 0 < n < k + 10 \dots \dots (3) \end{aligned}$

(1), (2), (3)をすべて満足する $k$ の範囲(4)を定めるため、 $k + 10$ と $\frac{75}{k}$ 、そして $15$ の大小関係を考える。

(i) $k + 10 < 15 ⟹ 0 < k < 5$
(i-a) $\frac{75}{k} < k + 10$
この条件を満たす $k$ の範囲を計算すると $k^{2} + 10 k - 75 < 0 ⟹ - 10 < k < 5$ なので(i)の条件を完全に含む。なのでこの条件下で(4)をすべて満たす $n$ は $0 < n < k + 10$ となり、これが12個であるには $k = 3$ である必要がある。\

(i-b) $\frac{75}{k} = k + 10$
この条件を満たす $k$ の値は5だが、この場合(4)は $0 < n < 15$ となるため問題の命題を満たさない。なので、この条件は考慮しない。
(i-c) $\frac{75}{k} > k + 10$
この条件を満たす $k$ の範囲は $k > 5$ であるが、(i)の条件との共通区間がない。なので、この条件は考慮しない。

(ii) $k + 10 > 15 ⟹ k > 5$
(ii-a) $\frac{75}{k} > k + 10$
この条件を満たす $k$ の範囲は $k > 5$ であるが、これは(ii)の条件と一致する。このとき(4)は $0 < n < k + 10$ となるが、 $k > 5$ ならこれを満たす自然数 $n$ は14個以上であるため問題の命題を満たさない。

(ii-b) $15 < \frac{75}{k} < k + 10$
$k > 5$ なら $15 k > 75, 15 > \frac{75}{k}$ なのでこの条件は生まれない。

(ii-c) $\frac{75}{k} < 15$
この条件を満たす $k$ の範囲は $k > 5$ であるが、これは(ii)の条件と一致する。このとき(4)は $0 < n < \frac{75}{k}$ となるが、これを満たす自然数 $n$ の数が12になるには $12 < \frac{75}{k} \leq 13 ⟹ \frac{75}{13} = 5 \frac{10}{13} \leq k < \frac{75}{12} = 6 \frac{1}{4}$ である必要があるため、自然数 $k = 6$ 。

なので $k$ は3または6であり、これらの和は $9$ . $◼$

15. 数学Ⅱ：導関数・定積分の応用（４点）

最高次項の係数が $1$ である三次関数 $f (x)$ と定数 $k (k \geq 0)$ に対し関数
$g (x) = {\begin{cases} 2 x - k & (x \leq k) \\ f (x) & (x > k) \end{cases}$
が次の条件を満たす。

(ア) 関数 $g (x)$ は実数全体の集合で増加し、微分可能である。
(イ) 全ての実数 $x$ に対して
$\int_{0}^{x} g (t) {| t (t - 1) | + t (t - 1)} d t \geq 0$ であり、
$\int_{3}^{x} g (t) {| (t - 1) (t + 2) | - (t - 1) (t + 2)} d t \geq 0$ である。

$g (k + 1)$ の最小値は？

16. 数学Ⅰ：対数関数（３点）

方程式 $\log_{2} (x + 1) - 5 = \log_{\frac{1}{2}} (x - 3)$ を満たす実数 $x$ の値を求めよ。

$\begin{aligned} \log_{2} (x + 1) - 5 = \log_{2} (x + 1) - \log_{2} 32 = \log_{2} \frac{x + 1}{32}, \\ \log_{\frac{1}{2}} (x - 3) = \log_{2^{- 1}} (x - 3) = \log_{2} (x - 3)^{- 1} = \log_{2} \frac{1}{x - 3} . \\ ∴ \frac{x + 1}{32} = \frac{1}{x - 3}, (x + 1) (x - 3) = 32, x^{2} - 2 x - 35 = 0, \end{aligned}$
$x = - 5 または x = 7.$
ただし、底の条件により $x - 3 > 0 ⟹ x > 3$ なので $x = 7 . ◼$

17. 数学Ⅱ：多項関数の積分法（３点）

関数 $f (x)$ に対し $f^{'} (x) = 6 x^{2} + 2$ であり $f (0) = 3$ であるとき、 $f (2)$ の値を求めよ。

$f (x) = \int f^{'} (x) d x - C^{'} = 2 x^{3} + 2 x + C, f (0) = C = 3,$
$∴ f (2) = 2 \times 2^{3} + 2 \times 2 + 3 = 23 . ◼$

18. 数学Ⅰ：数列・級数（３点）

$\sum_{k = 1}^{9} (a k^{2} - 10 k) = 120$ であるとき、定数 $a$ の値を求めよ。

$\begin{aligned} \sum_{k = 1}^{9} (a k^{2} - 10 k) & = a \sum_{k = 1}^{9} k^{2} - 10 \sum_{k = 1}^{9} k \\ = a \times \frac{9 \times 10 \times (2 \times 9 + 1)}{6} - 10 \times \frac{9 \times 10}{2} \\ = (19 \times 15 a) - 450 = 120. \end{aligned}$
両辺を15で割ると
$19 a - 30 = 8, a = 2 . ◼$

19. 数学Ⅱ：導関数・定積分の応用（３点）

時刻 $t = 0$ であるとき原点を出発し、数直線の上を動く点Pの時刻 $t (t \geq 0)$ での速度 $v (t)$ が
$v (t) = {\begin{cases} - t^{2} + t + 2 & (0 \leq t \leq 3) \\ k (t - 3) - 4 & (t > 3) \end{cases}$
である。出発した後点 $P$ の運動方向が二番目に変わる時刻での点 $P$ の位置が $1$ であるとき、正の実数 $k$ の値を求めよ。

時刻 $t$ での点Pの位置を $x (t)$ とすれば $x^{'} (t) = v (t)$ が成立するが、 $- t^{2} + t + 2 = 0$ を満たす正の実数 $t$ は $2$ のみであるため、2番目に運動方向が変わる時刻、つまり $x (t)$ が二番目の極値を持つ時刻 $t_{0}$ は区間 $[0, 3]$ では存在しないが、 $t > 3$ に対して $v (t)$ は常に増加し、 $lim_{t \to 3 +} v (t) = - 4 < 0$ なので $t_{0}$ は区間 $(3, \infty)$ で存在する。（区間の表記法に関しては20番の〈記号〉を参照願う。）

$x (t)$ の一般式を求める。 $x (t)$ は全ての実数 $t$ で連続でなければいけないので $lim_{t \to 3 -} x (t) = lim_{t \to 3 +} x (t)$ を成立させる実数 $C_{0}$ に対し
$\begin{aligned} x (t) & = {\begin{cases} \int_{0}^{t} (- s^{2} + s + 2) d s & (0 \leq t \leq 3) \\ \int_{0}^{t} {k (s - 3) - 4} d s + C_{0} & (t > 3) \end{cases} \\ = {\begin{cases} - \frac{1}{3} t^{3} + \frac{1}{2} t^{2} + 2 t & (0 \leq t \leq 3) \\ k (\frac{1}{2} t^{2} - 3 t) - 4 t + C_{0} & (t > 3) \end{cases} \end{aligned}$
である。 $lim_{t \to 3 -} x (t) = lim_{t \to 3 +} x (t)$ を用いて $C_{0}$ の値を求めると
$\begin{aligned} - 9 + \frac{9}{2} + 6 = k (\frac{9}{2} - 9) - 12 + C_{0} \\ \frac{3}{2} = C_{0} - 12 - \frac{9}{2} k \\ C_{0} = \frac{1}{2} (27 + 9 k) = \frac{9}{2} (k + 3) \end{aligned}$
となる。 $x (t)$ の式をまとめると
$x (t) = {\begin{cases} - \frac{1}{3} t^{3} + \frac{1}{2} t^{2} + 2 t & (0 \leq t \leq 3) \\ k (\frac{1}{2} t^{2} - 3 t) - 4 t + \frac{9}{2} (k + 3) & (t > 3) \end{cases}$
である。 $t_{0}$ の値は $v (t_{0}) = 0$ から $t_{0} = 3 + \frac{4}{k}$ なので、 $t_{0} > 3$ 、また $x (t_{0}) = 1$ から

$\begin{aligned} x (t_{0}) & = k {\frac{1}{2} {(3 + \frac{4}{k})}^{2} - 3 \times (3 + \frac{4}{k})} - 4 \times (3 + \frac{4}{k}) + \frac{9}{2} (k + 3) \\ = \frac{1}{2 k} {(3 k + 4)^{2} - 6 k (3 k + 4)} - 12 - \frac{16}{k} + \frac{9}{2} k + \frac{27}{2} \\ = - \frac{1}{2 k} (9 k^{2} - 16) + \frac{9}{2} k - \frac{16}{k} + \frac{3}{2} \\ = - \frac{8}{k} + \frac{3}{2} = 1, k = 16 . ◼ \end{aligned}$

20. 数学Ⅰ：三角関数（４点））

$5$ 以下の二つの自然数 $a, b$ に対して開区間 $(0, 2 π)$ で定義された関数 $y = a \sin x + b$ のグラフが直線 $x = π$ と交わる点の集合を $A$ とし、二つの直線 $y = 1, y = 3$ と交わる点の集合をそれぞれ $B, C$ とする。 $n (A \cup B \cup C) = 3$ になるようにする $a, b$ の順序対 $(a, b)$ に対し $a + b$ の最大値を $M$ 、最小値を $m$ とするとき、 $M \times m$ の値を求めよ。

〈記号〉
開区間 $a < x < b$ を $(a, b)$ と表し、閉区間 $a \leq x \leq b$ を $[a, b]$ と表す。片方に $=$ がなくとも同様に表す。
また、区間 $x > c$ は $(c, \infty)$ のように、 $x \leq d$ は $(- \infty, d]$ のように表す。 $=$ の有無が切り替わっても同様。

21. 数学Ⅱ：多項関数の微分法（４点）

最高次項の係数が $1$ である四次関数 $f (x)$ と次の条件を満たす。

(ア) $f^{'} (a) \leq 0$ である実数 $a$ の最大値は2である。
(イ) 集合 ${x | f (x) = k}$ の要素の個数が3以上になるようにする実数 $k$ の最小値は $\frac{8}{3}$ である。

$f (0) = 0, f^{'} (1) = 0$ であるとき、 $f (3)$ の値を求めよ。

22. 数学Ⅰ：数列（４点）

数列 ${a_{n}}$ は
$a_{2} = - a_{1}$
であり、 $n \geq 2$ であるすべての自然数 $n$ に対して
$a_{n + 1} = {\begin{cases} a_{n} - \sqrt{n} \times a_{\sqrt{n}} & (\sqrt{n} が自然数であり a_{n} > 0 である場合) \\ a_{n} + 1 & (その以外の場合) \end{cases}$
を満たす。 $a_{15} = 1$ になるようにするすべての $a_{1}$ の値の積を求めよ。

$a_{15} = a_{14} + 1 = \dots = a_{10} + 5$ である。

(i) $a_{9} \leq 0$ の場合を考える。

なら $a_{15} = a_{10} + 5 = a_{9} + 6 = \dots = a_{5} + 10$ なので、

(i-a) $a_{4} \leq 0$ の場合は

$a_{15} = a_{5} + 10 = a_{4} + 11 = \dots = a_{2} + 13 = - a_{1} + 13 = 1$ であるため、この場合の $a_{1}$ の値は $12$ である。
このときの数列 ${a_{n}}$ は ${12, - 12, - 11, \underset{a_{4}}{\underset{⏟}{- 10}}, - 9, - 8, - 7, - 6, \underset{a_{9}}{\underset{⏟}{- 5}}, - 4, - 3, - 2, - 1, 0, \underset{a_{15}}{\underset{⏟}{1}}, \dots}$ なので条件との矛盾もない。

(i-b) $a_{4} > 0$ の場合は

$a_{15} = a_{5} + 10 = a_{4} - 2 a_{2} + 10 = a_{3} - 2 a_{2} + 11 = 12 - a_{2} = 12 + a_{1} = 1$ であるため、この場合の $a_{1}$ の値は $- 11$ である。このときの数列 ${a_{n}}$ は ${- 11, 11, 12, \underset{a_{4}}{\underset{⏟}{13}}, - 9, - 8, - 7, - 6, \underset{a_{9}}{\underset{⏟}{- 5}}, - 4, - 3, - 2, - 1, 0, \underset{a_{15}}{\underset{⏟}{1}}, \dots}$
なので条件との矛盾もない。

(ii) $a_{9} > 0$ の場合を考える。

なら $a_{15} = a_{10} + 5 = a_{9} - 3 a_{3} + 5 = \dots = a_{5} - 3 a_{3} + 9$ なので、

(ii-a) $a_{4} \leq 0$ の場合は

$a_{15} = a_{5} - 3 a_{3} + 9 = a_{4} - 3 a_{3} + 10$ であるが、 $a_{4} = a_{3} + 1$ に注目すると
$a_{15} = a_{4} - 3 a_{3} + 10 = a_{4} - 3 (a_{3} + 1) + 7 = - 2 a_{4} + 7 = 1$
から $a_{4} = 3 > 0$ であることがわかり、これは条件との矛盾を起こす。なのでこの場合では $a_{15} = 1$ とさせる $a_{1}$ の値は存在しない。

(ii-b) $a_{4} > 0$ の場合は

$\begin{aligned} a_{15} & = a_{5} - 3 a_{3} + 9 \\ = a_{4} - 2 a_{2} - 3 a_{3} + 9 \\ = - 2 a_{3} - 2 a_{2} + 10 \\ = - 4 a_{2} + 8 \\ = 4 a_{1} + 8 = 1 \end{aligned}$
なのでこの場合の $a_{1}$ の値は $- \frac{7}{4}$ である。
このときの数列 ${a_{n}}$ は
${- \frac{7}{4}, \frac{7}{4}, \frac{11}{4}, \underset{a_{4}}{\underset{⏟}{\frac{15}{4}}}, \frac{1}{4}, \frac{5}{4}, \frac{9}{4}, \frac{13}{4}, \underset{a_{9}}{\underset{⏟}{\frac{17}{4}}}, - 4, - 3, - 2, - 1, 0, \underset{a_{15}}{\underset{⏟}{1}}, \dots}$
なので条件との矛盾もない。

これらの過程から $a_{1}$ の値は $12$ , $- 11$ , $- \frac{7}{4}$ であり、これらの積である答えは $231$ である。 $◼$

23. 確率と統計：場合の数（点）

四つの数字 $1, 1, 2, 3$ をすべて一列に並べる場合の数は？

24. 確率と統計：確率の演算（３点）

二つの事象 $A, B$ は互いに排反事象であり、
$P (A^{C}) = \frac{5}{6}, P (A \cup B) = \frac{3}{4}$
であるとき、 $P (B^{C})$ の値は？

〈記号〉
事象 $Q$ の余事象を $Q^{C}$ と表す。

25. 確率と統計：二項展開（３点）

多項式 $(x^{2} - 2)^{5}$ の展開式での $x^{6}$ の係数は？

26. 確率と統計：確率（３点）

文字 $a, b, c, d$ の中で重複を許可し $4$ 個を選び一列で並べて作ることのできるすべての文字列の中で任意で一つを選ぶとき、文字 $a$ が一つだけ含まれるか文字 $b$ が一つだけ含まれた文字列が選ばれる確率は？

27. 確率と統計：場合の数（３点）

$1$ から $6$ までの自然数が一つずつ書いてある $6$ 個の椅子が置いてある。この $6$ 個の椅子を一定の間隔を置いて円形に並べるとき、両隣の椅子に書いてある数の和が $11$ にならないように並べる場合の数は？
（ただし、回転して一致するものは同じものと見なす。）
PS 27番

28. 確率と統計：条件付き確率（４点）

机に置いてある $4$ 個の硬貨に対して次の試行をする。

4個の硬貨のうち、任意で一つの硬貨を選び一回裏返す。

最初に $3$ 個の硬貨は表が見えるように、 $1$ 個の硬貨は裏が見えるように置いてある。上記の試行を $5$ 回繰り返した後 $4$ 個の硬貨が総て同じ面が見えるように置いてあるとき、すべて表が見えるように置いてある確率は？

（図省略）

29. 確率と統計：確率（４点）

$40$ 個のボールが入っている袋がある。それぞれのボールは白いボールか黒いボールの中の一つである。

この袋から任意で $2$ 個のボールを同時に取り出すとき、白いボール $2$ 個を取り出す確率を $p$ 、白いボール1個と黒いボール $1$ 個を取り出す確率を $q$ 、黒いボール $2$ 個を取り出す確率を $r$ とする。 $p = q$ であるとき、 $60 r$ の値を求めよ。（ただし、 $p > 0$ である。）

30. 確率と統計：場合の数：関数の個数（４点）

集合 $X = {- 2, - 1, 0, 1, 2}$ に対して次の条件を満たす関数 $f : X ⟶ X$ の個数を求めなさい。

(ア) $X$ の全ての要素 $x$ に対して $x + f (x) \in X$ である。
(イ) $x = - 2, - 1, 0, 1$ であるとき $f (x) \geq f (x + 1)$ である。

23. 微積分：数列の極限（２点）

$lim_{n \to \infty} \frac{{(\frac{1}{2})}^{n} + {(\frac{1}{3})}^{n + 1}}{{(\frac{1}{2})}^{n + 1} + {(\frac{1}{3})}^{n}}$ の値は？

24. 微積分：陰関数の微分法（３点）

曲線 $x \sin 2 y + 3 x = 3$ の上の点 $(1, \frac{π}{2})$ での接線の傾きは？

25. 微積分：関数の極限（点）

数列 ${a_{n}}$ が
$\sum_{n = 1}^{\infty} (a_{n} - \frac{3 n^{2} - n}{2 n^{2} + 1}) = 2$
を満たすとき、 $lim_{n \to \infty} (a_{n}^{2} + 2 a_{n})$ の値は？

26. 微積分：数列の極限（３点）

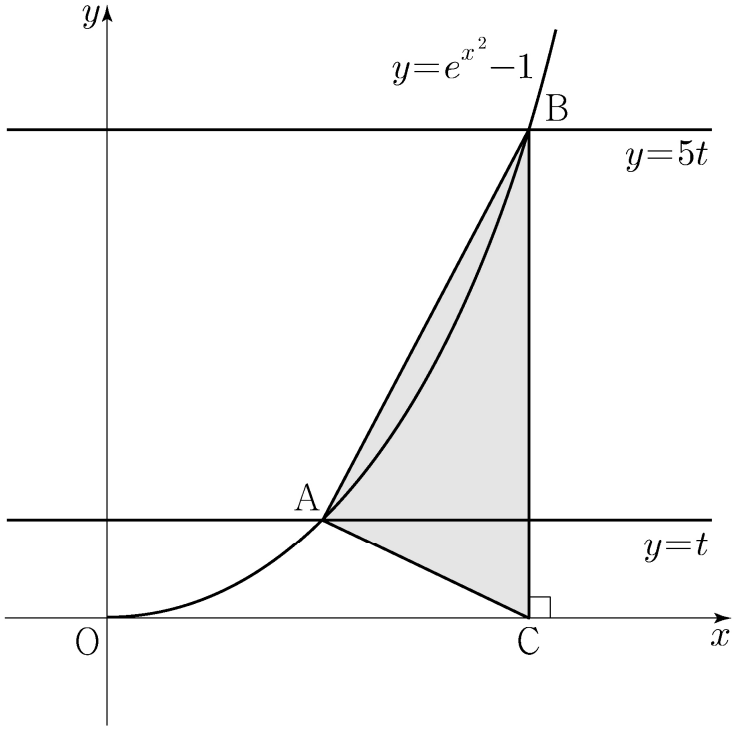
正の数 $t$ に対して曲線 $y = e^{x^{2}} - 1 (x \geq 0)$ が二つの直線 $y = t, y = 5 t$ と交わる点をそれぞれ $A, B$ とし、点 $B$ で $x$ 軸に下ろした垂線の足を $C$ とする。三角形 $A B C$ の面積を $S (t)$ とするとき、 $lim_{t \to 0 +} \frac{S (t)}{t \sqrt{t}}$ の値は？
CC 26番

27. 微積分：導関数の応用（３点）

定数 $a (a > 1)$ と実数 $t (t > 0)$ に対して曲線 $y = a^{x}$ 上の点 $A (t, a^{t})$ での接線を $l$ とする。点 $A$ を通り直線 $l$ に垂直である直線が $x$ 軸と交わる点を $B$ , $y$ 軸と交わる点を $C$ とする。 $\frac{\overset{―}{A C}}{\overset{―}{A B}}$ の値が $t = 1$ で最大であるとき、 $a$ の値は？

28. 微積分：関数の連続・導関数（４点）

関数 $f (x)$ が
$f (x) = {\begin{cases} (x - a - 2)^{2} e^{x} & (x \geq a) \\ e^{2 a} (x - a) + 4 e^{a} & (x < a) \end{cases}$
であるとき、実数 $t$ に対し $f (x) = t$ を満たす $x$ の最小値を $g (t)$ とする。

関数 $g (t)$ が $t = 12$ でのみ不連続であるとき、 $\frac{g^{'} (f (a + 2))}{g^{'} (f (a + 6))}$ の値は？
（ただし、 $a$ は定数である。）

29. 微積分：関数の連続・微分可能性（４点）

関数 $f (x) = \frac{1}{3} x^{3} - x^{2} + \ln (1 + x^{2}) + a$ （ $a$ は定数）と二つの正の数 $b, c$ に対して関数
$g (x) = {\begin{cases} f (x) & (x \geq b) \\ - f (x - c) & (x < b) \end{cases}$
は実数全体の集合で微分可能である。

$a + b + c = p + q \ln 2$ であるとき、 $30 (p + q)$ の値を求めよ。

（ただし、 $p, q$ は有理数であり、 $\ln 2$ は無理数である。）

記号
自然対数関数、つまり底がネイピア数 $e = lim_{x \to 0 +} (1 + x)^{1 / x}$ である対数関数 $\log_{e} x$ を $\ln x$ と表す。

30. 微積分：数列の極限（４点）

関数 $y = \frac{\sqrt{x}}{10}$ のグラフと関数 $y = \tan x$ のグラフが交わるすべての点の $x$ 座標を小さい数から並べたとき、 $n$ 番目の数を $a_{n}$ とする。
$\frac{1}{π^{2}} \times lim_{n \to \infty} a_{n}^{3} \tan^{2} (a_{n + 1} - a_{n})$
の値を求めなさい。