IMO2019P6の一般化について
かえでです.今回はふと気付きを得たのでIMO2019P6 (ISL2019G7) について超短めの記事を書こうと思います.
本題
まず,IMO2019P6の主張を載せます.
$AB \neq AC$なる鋭角三角形$ABC$について,その内心を$I$とし,内接円$\omega$が$BC,CA,AB$と接する点をそれぞれ$D,E,F$とする.$D$を通り直線$EF$に垂直な直線が$\omega$と再び交わる点を$R$とし,直線$AR$と$\omega$が再び交わる点を$P$,円$PCE$と円$PBF$が再び交わる点を$Q$とする.このとき,直線$PQ$と直線$DI$は$A$を通り直線$AI$に垂直な直線上で交わることを示せ.
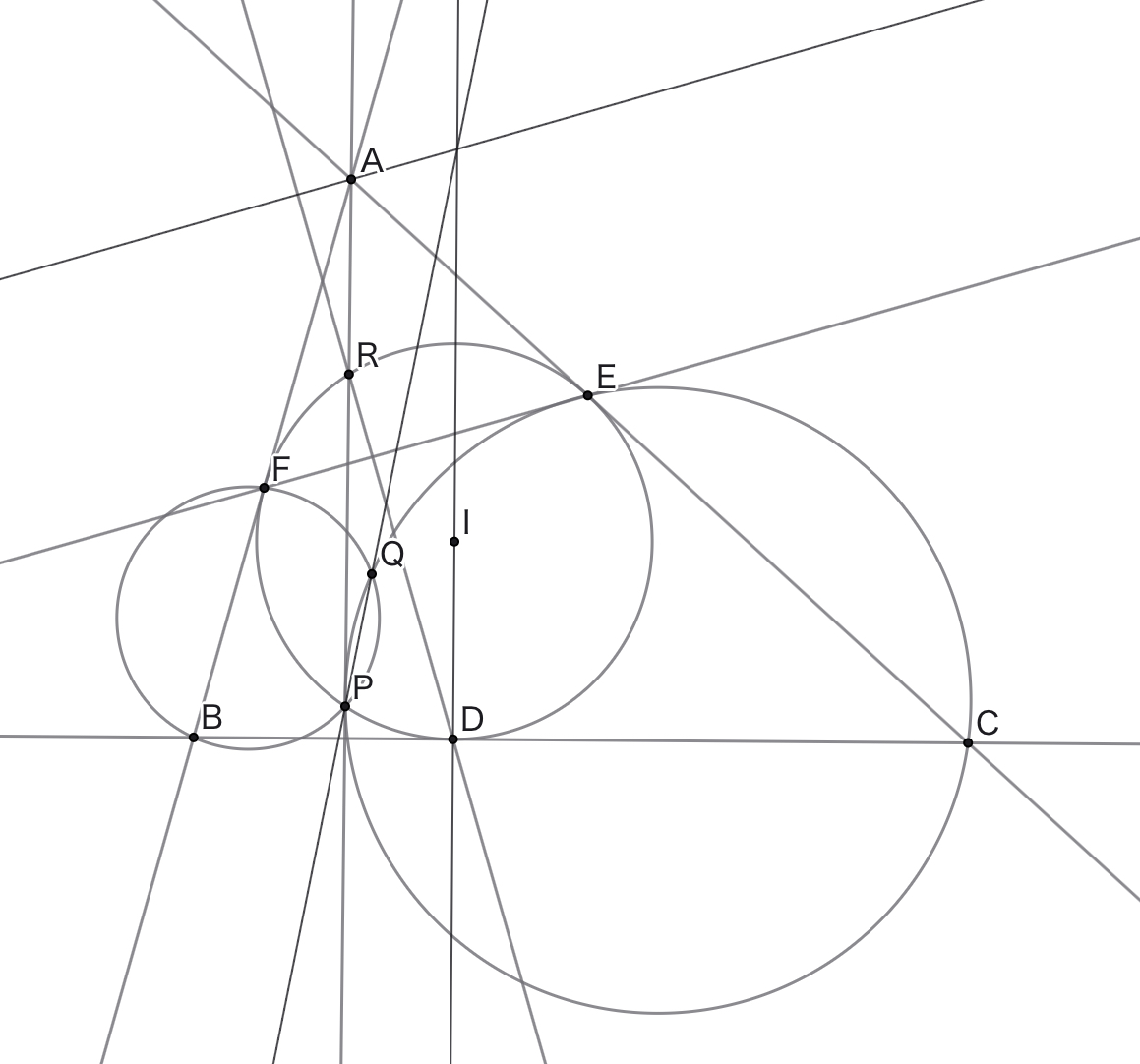 オリジナル
オリジナル
明らかに一般化が出来そうな見た目ですが,実際にTran Quang Hungというベトナムの幾何の達人の方が次のような一般化を与えています.
三角形$ABC$と辺上にない点$P$について,その垂足三角形を$DEF$とし,円$DEF$と直線$BC$が再び交わる点を$X$とする.$X$を通り直線$EF$に垂直な直線と円$DEF$が再び交わる点を$R$とし,直線$AR$と$\omega$が再び交わる点を$S$,円$CSF$と円$BSE$が再び交わる点を$T$とする.このとき,直線$ST$と直線$PD$は$A$を通り直線$EF$に平行な直線上で交わる.
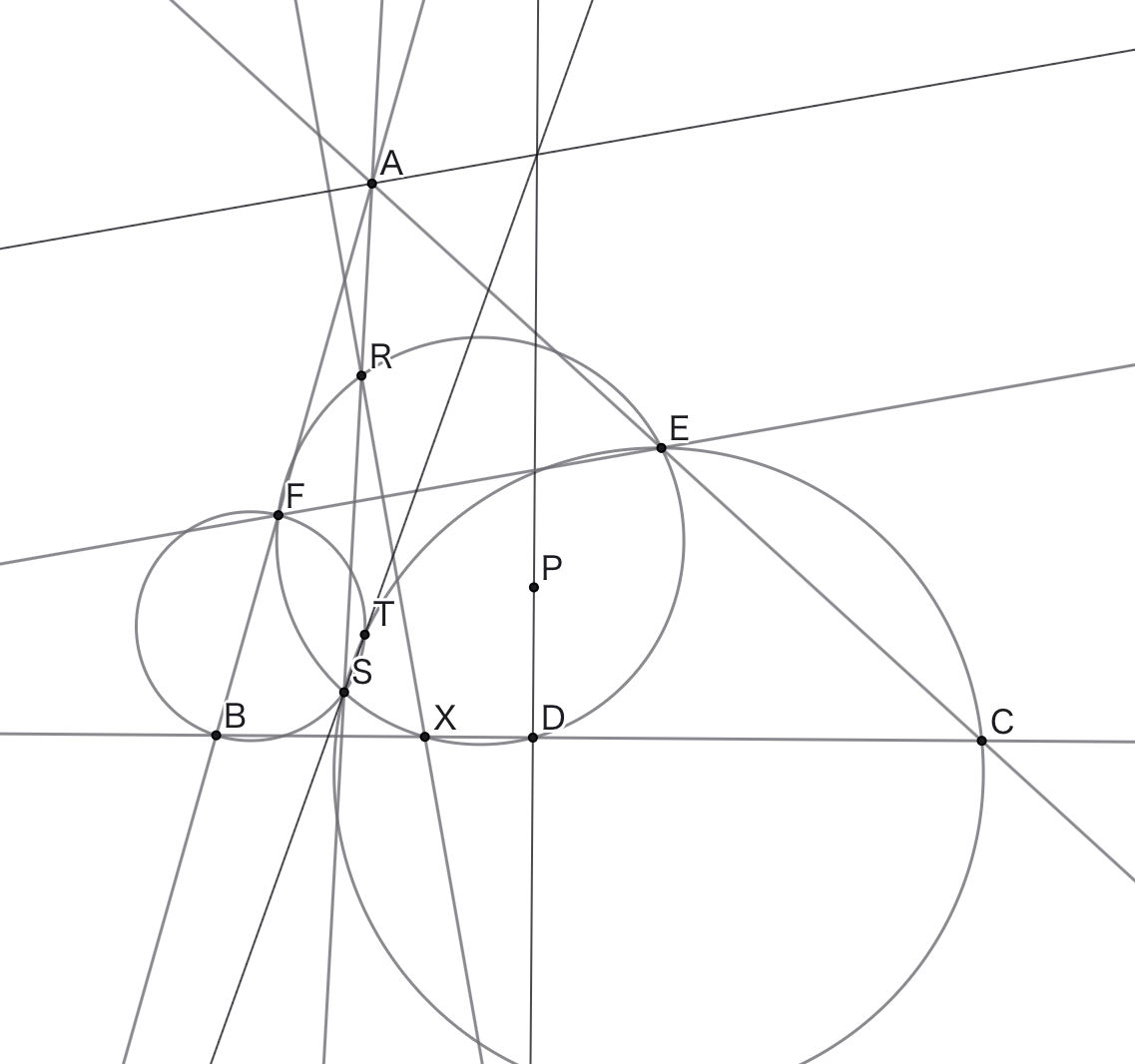 一般化
一般化
惚れ惚れするくらいあまりに綺麗な一般化すぎてずっと図を見てられますよね.証明は
Tran Quang Hungの投稿(pdf)
にあります.この証明がまた完璧で美しいんですよね.
さて,ところで3日前に私はこのTranによる一般化にさらなる一般化の余地を感じて,垂足三角形の部分をisologicなどを使って一般化できないかと試していました.その結果次の一般化が産物として出てきました.
三角形$ABC$と点$P$および直線$BC$上の点$D$について,円$CDP$と直線$AC$が再び交わる点を$E$,円$BDP$と直線$AB$が再び交わる点を$F$とし,直線$PD$が円$DEF$と再び交わる点を$X$とする.$X$を通り直線$EF$に平行な直線と円$DEF$が再び交わる点を$R$とし,直線$AR$が円$DEF$と再び交わる点を$S$,円$CSE$と円$BSF$が再び交わる点を$T$とする.このとき,直線$ST$と直線$PD$は$A$を通り直線$EF$に平行な直線上で交わる.
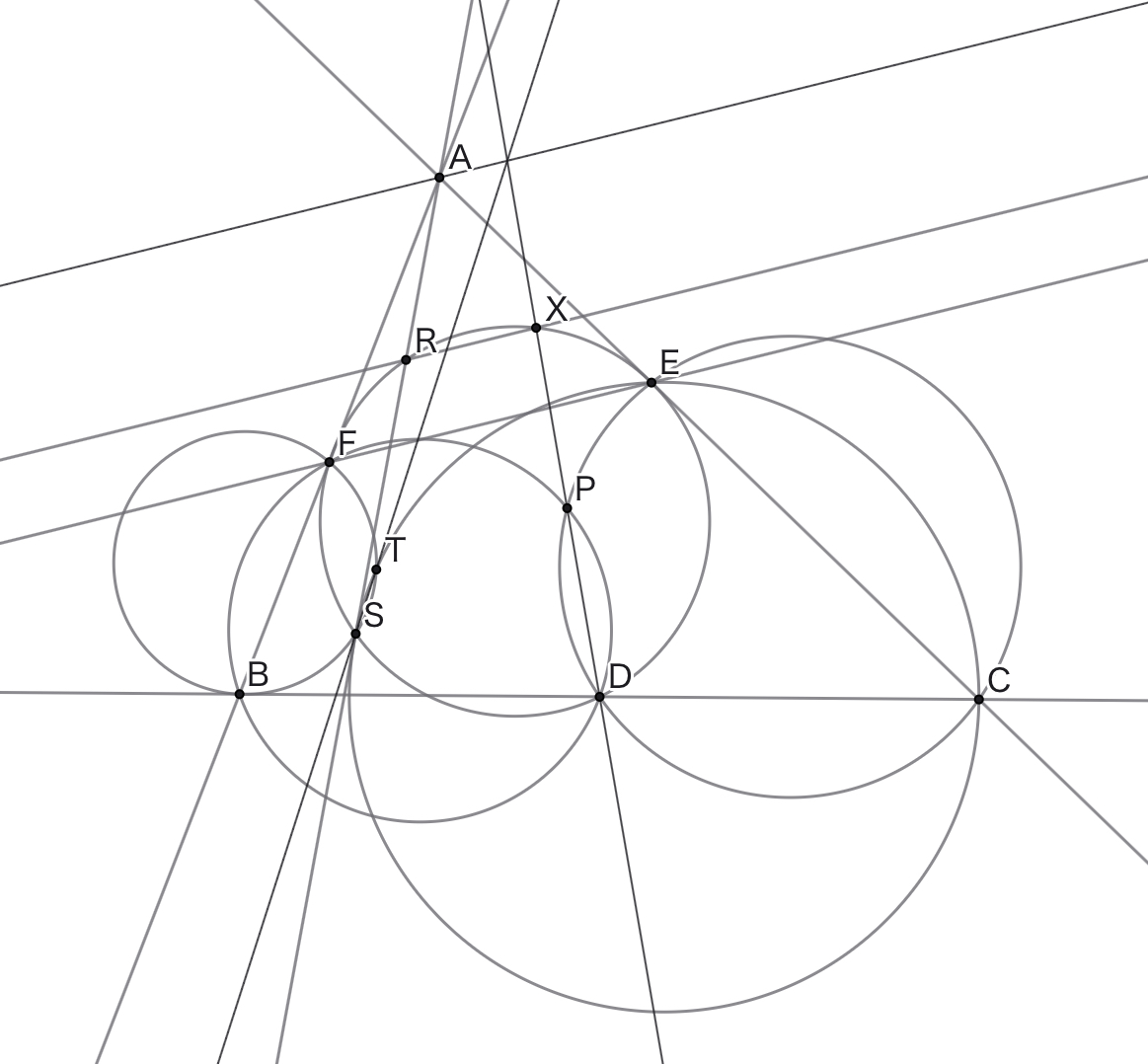 原題はとっくにオーバーキルされている
原題はとっくにオーバーキルされている
なるほど,点$D$は直線$BC$上ならどこでもよかったんですね.証明も先ほどのTranによる証明と全く同様にやれば出来ます.しかし,先ほど私はもっと強い主張が成り立つことに気づきました.
三角形$ABC$と点$P,D$について,円$CDP$と直線$AC$が再び交わる点を$E$,円$BDP$と直線$AB$が再び交わる点を$F$とし,直線$PD$が円$DEF$と再び交わる点を$X$とする.$X$を通り直線$EF$に平行な直線と円$DEF$が再び交わる点を$R$とし,直線$AR$が円$DEF$と再び交わる点を$S$,円$CSE$と円$BSF$が再び交わる点を$T$とする.このとき,直線$ST$と直線$PD$は$A$を通り直線$EF$に平行な直線上で交わる.
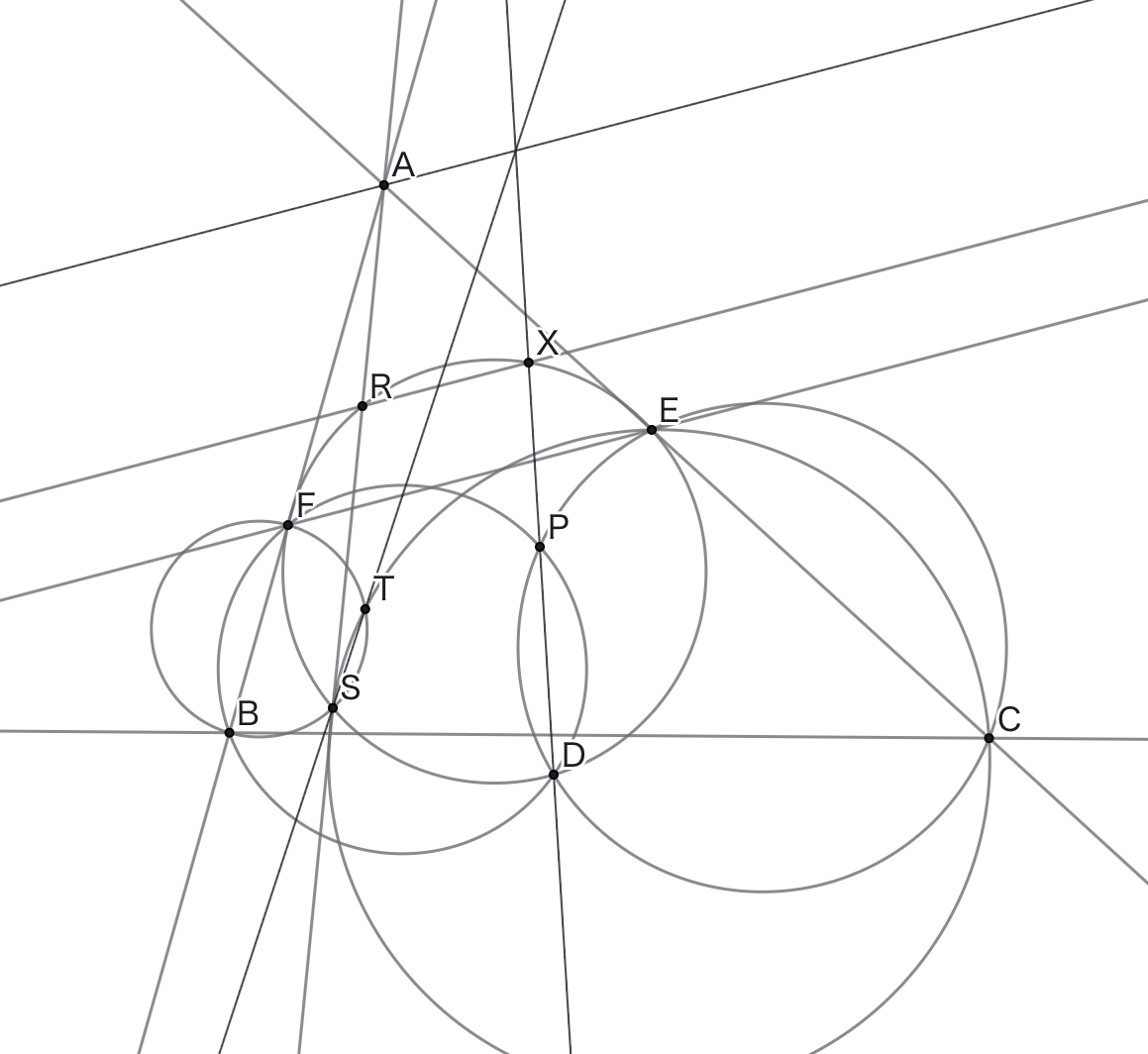 おお
おお
いや直線$BC$上じゃなくても成り立つんかいと見つけた時になりました.そして,また証明があのTranによる証明とほぼ全て同様にできるんですよね.
ということで以上ここ数日間にあったギャグのような発見と展開でしたが,実はこれかなり強いんですよね.例えばもちろんIMO2019P6は系として示せますし,内心を3つの傍心に変えたものも示せます.そしてDumpty pointやHumpty pointの性質も系として示せますね.
最後に
では,この短い記事の最後にまた別のIMO2019P6の一般化をについて書いて終わろうと思います.これはLin_yangyuanというAoPSユーザーが2019年7月に投稿して現在も誰も証明できていない一般化です.
三角形$ABC$と定点$U,I$および直線$AC,AB$上の定点$E,F$について,円$BFI$と円$CEI$が再び交わる点を$D$とし,円$DEF$上に点$P$を取る.円$BFP$と円$CEP$が再び交わる点を$Q$とし,直線$PQ$と直線$DI$の交点を$S$とする.直線$US$と円$SDP$が再び交わる点を$T$とするとき,点$P$に依らず点$T$はある定円$\omega$上に乗るので,円$\omega$と円$SDP$が再び交わる点を$K$とし,直線$AK$と$\omega$が再び交わる点を$V$とする.このとき,直線$EF$と直線$UV$は常に平行である.
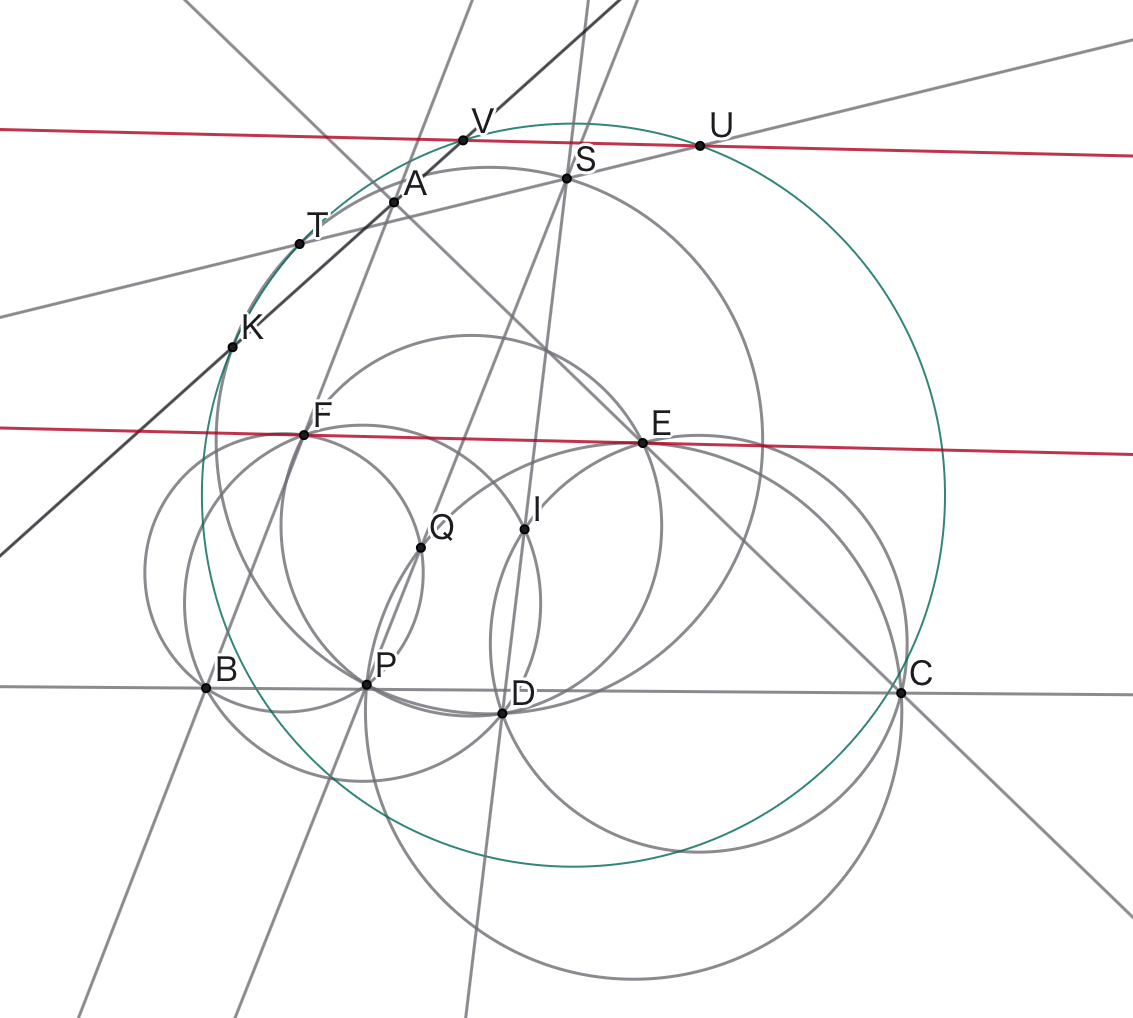 ヤバい
ヤバい
これまじでヤバいです.ありえないくらい強くて,当然のように僕がさっき与えた一般化の一般化の一般化を系として含んでいます.あと,シンプルに複雑すぎて何がどうなっているかも分からないですね.証明できた方や更なる一般化を発見できた方はぜひ
Lin_yangyuanの引用元ポスト
に投稿してみてください.
では,以上です.
