三角関数の方程式〜京大文系2012第5問の改題〜

解答

まず$(\ast)$を満たす$\theta$が存在する正の実数の組$(a, b)$の条件を求める。$a>0, b>0$に注意して以下議論する。
\begin{align*} \sin{a\theta}=\cos{b\theta}&\iff \sin{a\theta}=\sin\left(\dfrac{\pi}{2}-b\theta\right)\\ &\iff a\theta=\dfrac{\pi}{2}-b\theta+n\pi となる整数nが存在する。\\ &\iff \theta=\dfrac{2n+1}{2(a+b)}\pi となる整数nが存在する。 \end{align*}
よって, $(\ast)$を満たす$\theta$が存在することは
\begin{align*} 0<\dfrac{2n+1}{2(a+b)}\pi\leqq{\pi} \end{align*}
を満たす整数$n$が存在することと同値である。これは
\begin{align*} 0<\dfrac{2n+1}{2(a+b)}\pi\leqq{\pi} \end{align*}
を
\begin{align*} 0< n\leqq{\dfrac{2(a+b)-1}{2}} \end{align*}
と整理できるから
\begin{align*} \dfrac{2(a+b)-1}{2}\geqq{1} \end{align*}
と言い換えられる。つまり
\begin{align*} 2a+2b-3\geqq{0} \end{align*}
である。よって, 求める$(a, b)$の条件は
\begin{align*} a>0かつb>0かつかつ2a+2b-3<3 \end{align*}
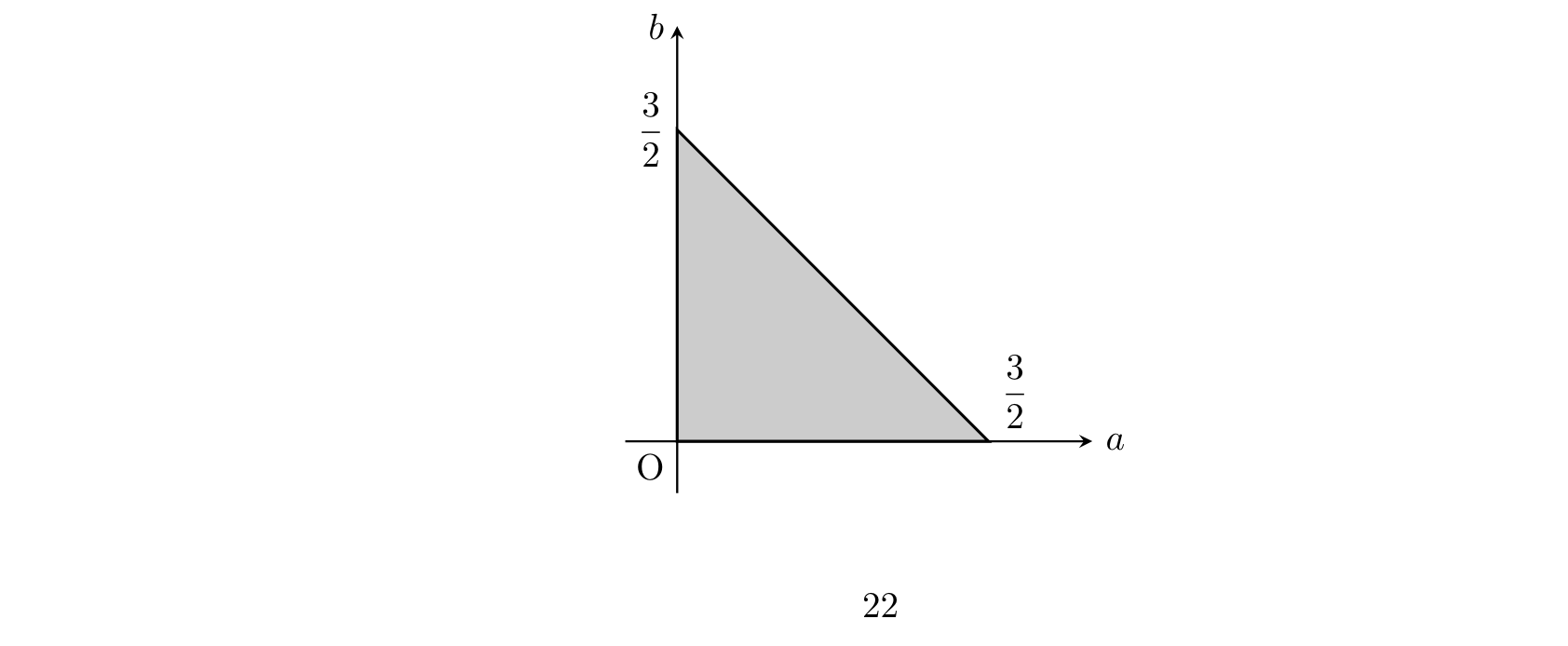
である。これを座標平面上に図示すると, 以下の灰色部分になるが境界は含めない。