第二回四国中国数学コンテスト　解説

783

ここでは,私とRankTurnipが主催する第二回四国中国数学コンテストの全問題の解説を紹介しようと思います.

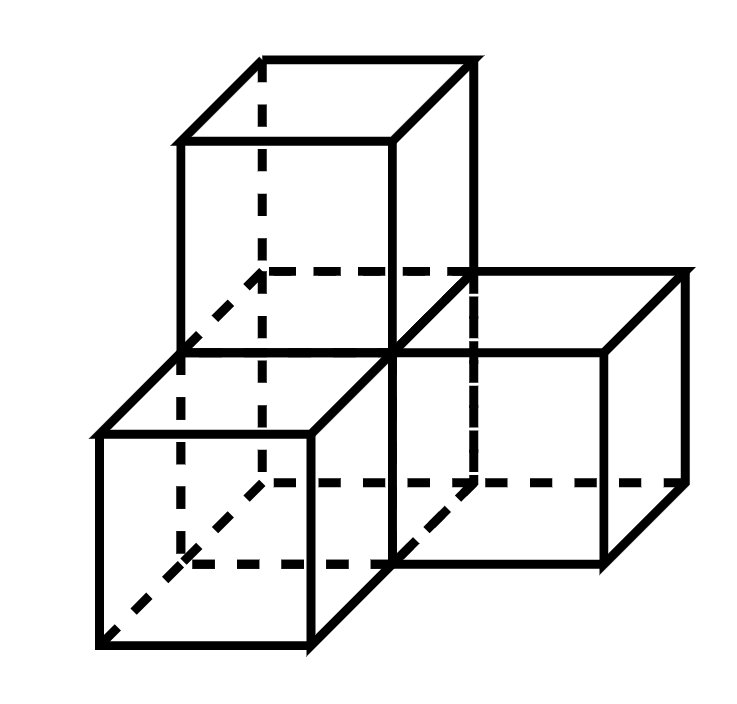
次のような $1 \times 1 \times 1$ の立方体 $4$ つを組み合わせて作ったブロックをいくつか(重なりなく)用いることによって $2023 \times 2024 \times 2025$ の直方体の内部を隙間なく充填することは可能か.

解説.

$2023 \times 2024 \times 2025$ の直方体を $1 \times 1 \times 1$ の立方体で埋め尽くすことを考えよう.このとき $2023 \times 2025$ の面を底面として左下から数えて奇数行、奇数列、奇数段のものと偶数行、偶数列、偶数段のものがあった場所を黒く塗りつぶすことを考える.このとき,ブロックはつねにちょうど $1$ つの黒く塗られた立方体と共通部分をもつのでこのブロックを置く個数はこの黒く塗られた立方体の個数と一致するが,この黒く塗られた立方体の個数は $\frac{2023 \times 2024 \times 2025}{4}$ と一致しないので矛盾.よってこのような操作は不可能であることが示される.

正の有理数に対して定義され正の有理数値をとる関数 $f$ であって，任意の正の有理数 $x, y$ に対して $f (x y) + f (x) + f (y + 1) = f (x) f (y) + 3$ を満たすものをすべて求めよ.

解説.

$x, y$ への代入を $P (x, y)$ とする. $P (x, y), P (y, x)$ より, $f (x + 1) - f (x) = c (c は定数)$ . これより $n \in Z^{+}$ で $f (n) = c (n - 1) + f (1)$ . $x, y \in Z^{+}$ について, これを与式に適用すると $(c, f (1)) = (1, 2)$ を得る. これより, $f (x) = x + 1 (x \in Z^{+})$ がわかる. 正整数 $x, y$ について $P (\frac{x}{y}, y)$ より $f (\frac{x}{y} \cdot y) + f (\frac{x}{y}) + f (y + 1) = f (\frac{x}{y}) f (y) + 3 ⟺ f (\frac{x}{y}) = \frac{x}{y} + 1$ . したがって, $f (x) = x + 1 (x \in Q^{+})$ .

三角形 $A B C$ において，その内接円を $ω$ ， $∠ A$ 内の傍接円を $Ω$ とする． $ω, Ω$ と $B C$ の接点をそれぞれ $D, D^{'}$ とし，直線 $A D$ と $Ω$ の交点のうち， $A$ により近い方を $G$ とする． $3$ 点 $G, D, D^{'}$ を通る円と $ω$ の交点であって $D$ でないものを $H$ としたとき， $3$ 点 $A, H, D^{'}$ は共線であることを示せ

解説.

三角形 $A B C$ の内心を $I$ とし， $Ω$ における $D^{'}$ の対蹠点を $S$ とする．いま， $S$ における $Ω$ の接線は明らかに直線 $B C$ と平行であるから， $ω$ を $Ω$ に移す $A$ を中心とする相似拡大を考えることにより， $A, D, S$ は共線である．したがって， $∠ D G D^{'} = 180^{\circ} - ∠ S G D^{'} = 90^{\circ}$ であるから， $∠ D H D^{'} = 90^{\circ}$ である．よって，線分 $D D^{'}$ の中点を $M$ とすればこれは円 $D H D^{'}$ の中心である．これまでの結果より，直線 $H D^{'}$ と直線 $I M$ は平行であるから， $D$ を中心として直線 $I M$ を2倍に拡大することにより，直線 $D^{'} H$ が $ω$ における $D$ の対蹠点 $K$ を通ることが分かる． $A, D^{'}, S$ の共線から $A, K, D^{'}$ の共線が明らかに従うから先述の結果と併せて $A, K, H, D^{'}$ の共線が従い，特に題意は示される．

任意の正整数 $k, m$ に対して，ある正整数 $n$ が存在して， $2^{n} + n^{2} + k$ が $m$ 種類以上の相異なる素数で割り切れることを示せ．

解説.

$f (n) = 2^{n} + n^{2} + k$ とする. $f (1)$ と $f (2)$ のいずれかは奇数であるので,そのようなものを $f (c)$ とする.ここで $f (c)$ を割り切る素因数を一つとってきてそれを $p_{1}$ とする.ここでフェルマーの小定理と $L T E$ の補題から $2^{((p_{1} - 1) p_{1}^{v_{p_{1}} (f (c)) + 1})} \equiv 1 (\mod p_{1}^{v_{p_{1}} (f (c)) + 1})$ であることから $2^{c} \equiv 2^{c + ((p_{1} - 1) p_{1}^{v_{p_{1}} (f (c)) + 1})} (\mod p_{1}^{v_{p_{1}} (f (c)) + 1})$ $c^{2} \equiv (c + ((p_{1} - 1) p_{1}^{v_{p_{1}} (f (c)) + 1}))^{2} (\mod p_{1}^{v_{p_{1}} (f (c)) + 1})$ より $f (c) \equiv f (c + (p_{1} - 1) p^{v_{p_{1}} (f (c)) + 1})) (\mod p_{1}^{v_{p_{1}} (f (c)) + 1})$ である.よって $v_{p} (f (c)) = v_{p} (f (c + (p_{1} - 1) p^{v_{p_{1}} (f (c))} + 1))$ であり,かつ $f (c) < f (c + (p_{1} - 1) p^{(v_{p_{1}} (f (c)) + 1})$ から $f (c + (p_{1} - 1) p^{v_{p_{1}} (f (c)) + 1}))$ は $p_{1}$ でない素因数をもつ.ここで関数 $g (n)$ を次のように定義しよう. $g (1) = (p_{1} - 1) p_{1}^{v_{p_{1}} (f (c)) + 1}, g (n + 1) = g (n) \times (p_{n + 1} - 1) p_{n + 1}^{v_{p_{n + 1}} (f (c + \sum_{k = 1}^{n} g (k)) + 1}$ このとき $p_{n}$ は $f (c + \sum_{k = 1}^{n - 1} g (k))$ に含まれる素因数であって $p_{1}, p_{2} . . . p_{n - 1}$ でないものである.(このような $p_{n}$ が取れることは一連の議論より従う.)ここで $f (c + \sum_{k = 1}^{m - 1} g (k))$ は少なくとも $p_{1}, p_{2} . . . p_{m}$ で割り切れるので示された.

正整数 $n$ に対して， $S = {1, 2, 3, . . ., n}$ とする． $S$ の任意の部分集合に対して定義され $S$ の部分集合を対応付ける規則 $F$ であって，任意の $S$ の部分集合 $A ， B$ に対して $F (A \cup B) = F (A) \cup F (B)$ を満たすものの個数を求めよ.

解説.

$B$ に $\emptyset, S$ を代入することによって任意の $S$ の部分集合 $A$ に対して $F (\emptyset) \subset F (A) \subset F (S)$ がわかる.ここで $S$ の要素 $p, a, b$ であって次の条件を満たすようなものが存在すると仮定しよう. $p \in F (A) ⟹ {a, b} \subset A$ ここで集合 $X$ を $A$ の要素であって $a$ でないもの全体の集合とする.このとき与式から $p \in F ({a}) \cup F (X)$ となるはずだがこれは仮定に矛盾.よってこのような要素の組は存在しないことがわかる.ここから $S$ の任意の要素 $x$ は $x \in F (S)$ ならば $S$ のある要素 $r$ が存在して $x \in F ({r})$ となる.よって全ての $x$ それぞれに対して $x \in F (\emptyset)$ とするか $x \notin F (\emptyset)$ かつ $2^{n}$ 通りの $x \in F ({r})$ なる $r$ の部分集合を定めれば $F$ は $1$ 意に定まり,このとき確かに条件をみたすので求める $F$ の個数は $(2^{n} + 1)^{n}$ 個である.

$3^{n} - 2^{n} - 1$ が平方数となるような正整数 $n$ をすべて求めよ．

解説.

条件は $3^{n} - 2^{n} - 1 = a^{2}$ なる整数 $a$ が存在することと同値である.このとき $3^{n} - 2^{n} = a^{2} + 1$ となるので $3^{n} - 2^{n}$ は $4$ で割って $3$ 余る素因数を持たない.このとき $n$ がある奇素数 $p$ で割りきれると仮定すると $3^{n} - 2^{n}$ は $3^{p} - 2^{p}$ を約数に持ち, $3^{p} - 2^{p} \equiv 3^{p} \equiv 3 (\mod 4)$ よりこれは $4$ で割って $3$ あまる素因数で割り切れるので矛盾.よって $n$ はある非負整数 $k$ を用いて $n = 2^{k}$ とあらわすことができる.ここで式を以下のように変形する. $3^{2^{k}} - 1 = 2^{2^{k}} + a^{2}$ $k = 0, 1, 2$ のときは条件を満たす整数 $a$ が存在する.以下 $k > 2$ と仮定する.LTEの補題より $v_{2} (左辺) = k + 2$ . $k > 2$ より $2^{k} > k + 2$ であるので $v_{2} (右辺) = v_{2} (a^{2}) = k + 2$ であり, $v_{2} (a) = \frac{k}{2} + 1$ である.ここで再び式を以下のように変形する. $(3^{2^{k - 1}} - a) (3^{2^{k - 1}} + a) = 2^{2^{k}} + 1$ このとき左辺を割り切る任意の素数 $p$ について $2^{2^{k}} \equiv - 1 (\mod p), 2^{2^{k + 1}} \equiv 1 (\mod p)$ であることから $\mod p$ における $2$ の位数が $2^{k + 1}$ であることが分かるので $p \equiv 1 (\mod 2^{k + 1})$ である.しかし $3^{2^{k - 1}} \equiv 1 (\mod 2^{k + 1})$ と $v_{2} (a) = \frac{k}{2} + 1 < k + 1$ から $(3^{2^{k - 1}} - a) ≢ 1 (\mod 2^{k + 1})$ であるので $3^{2^{k - 1}} - a$ は $p ≢ 1 (\mod 2^{k + 1})$ なる素因数 $p$ をもち矛盾.以上より $n = 1, 2, 4$ である.