超 絶対絶命 でんぢゃらSUSYさん

はじめに

Merry Christmas!
soleilと申します。
この度はPhysics lab 2026アドベントカレンダー25日目の場をお借りして 作曲家 に引き続き漫画家に挑戦する運びとなりました。

さらに今日はクリスマス！
良い子にしていたのに、誰からもプレゼントをもらえなかったそこのあなたにでんぢゃらSUSYさんからのプレゼントを！

Merry Christmasなのじゃ！

対称性を拡張するのじゃっ!

第一話

じ）孫、Kaluza-Klein理論ってのを知っておるか？

孫）知らないよ〜それは何？

じ）時空を5次元に拡張して、spinが0,1,2のHiggs場のようなスカラー場、電磁場、重力場を統一するんじゃ
5次元時空の計量$g_{MN},(M,N=0,1,\cdots 4)$を考え、1つの次元（今回は第4成分）をすごい小さいとするといつもの4次元時空では

$g_{44}=\phi,g_{\mu4}=A_{\mu}, g_{\mu\nu} \ \ (\mu,\nu = 0,1,2,3)$

のようにそれぞれスカラー場(spin$0$)、ベクトル場(spin$1$)、テンソル場(spin$2$)が出てくるんじゃ
このことから時空の構造を変えることで、整数スピンを統一的に扱う理論が作れたんじゃ
（実はこれらがそのままHiggs場,gauge場,重力場になるという素朴な期待は残念ながら正しくないんじゃ...
でもこのような次元を大きくし、それにより4次元の理論を説明する余剰次元のアイデアは現在の最先端の理論（弦理論など）へも引き継がれておるんじゃぞ）

孫）でもおじいちゃん
対称性を拡張するって言っても、4次元時空では物理的な系の対称性がPoincare対称性とGauge対称性に限られるっていうNo-Go theorem
Coleman-Mandulaの定理 があるって聞いたことあるよ！？

じ）孫、実はそれは交換関係がbosonic$[A,B]=AB-BA$な時であることを仮定しとるんじゃ！
ワシはfermionicな反交換関係${A,B}=AB+BA$を使うんじゃ！
これは後で見るように時空に反可換な座標を入れた超時空を考えていることに対応しているんじゃ

孫）でも時空が反交換なんて意味わからないよ

じ）こんなので意味わかんないと言ってるようじゃまだまだじゃの〜
こっからもっとたくさん意味わからないもんが出てくるんじゃ
いいからまずは反可換な座標を導入してみるのじゃ！！
反可換な座標を作るために、まずは反可換な時空への並進演算子、つまり微小変換の生成子を作ってそこから有限に広げていくように考えていくのじゃ

bosonの従う運動方程式Klein-Gordon方程式は知っとるか？

$(\partial_\mu \partial^\mu-m^2)\phi =0$

ここからfermionの運動方程式を導くとき、”因数分解”をしてDirac方程式を導く話を思い出すんじゃ！

$ (i\gamma^\mu\partial_\mu - m)\psi = 0$

この"因数分解"でbosonからfermion話を今度は時空に当てはめて考えてみるのじゃ
時空の微小変換は運動量じゃったな
ではこの運動量の因数分解、"平方根$\sqrt{\hat{P}_\mu}$"を考えるのじゃ
じゃから超対称性は運動量のような時空の対称性の一種なんじゃ！

孫）...

じ）なんじゃ疑っておるんか？
ここからよーく見ておれ
反交換関係は
$\{A,B\}\coloneqq AB+BA$
じゃったな
$A=B$ならほぼ二乗じゃな！
じゃからこんな代数を考えるんじゃ
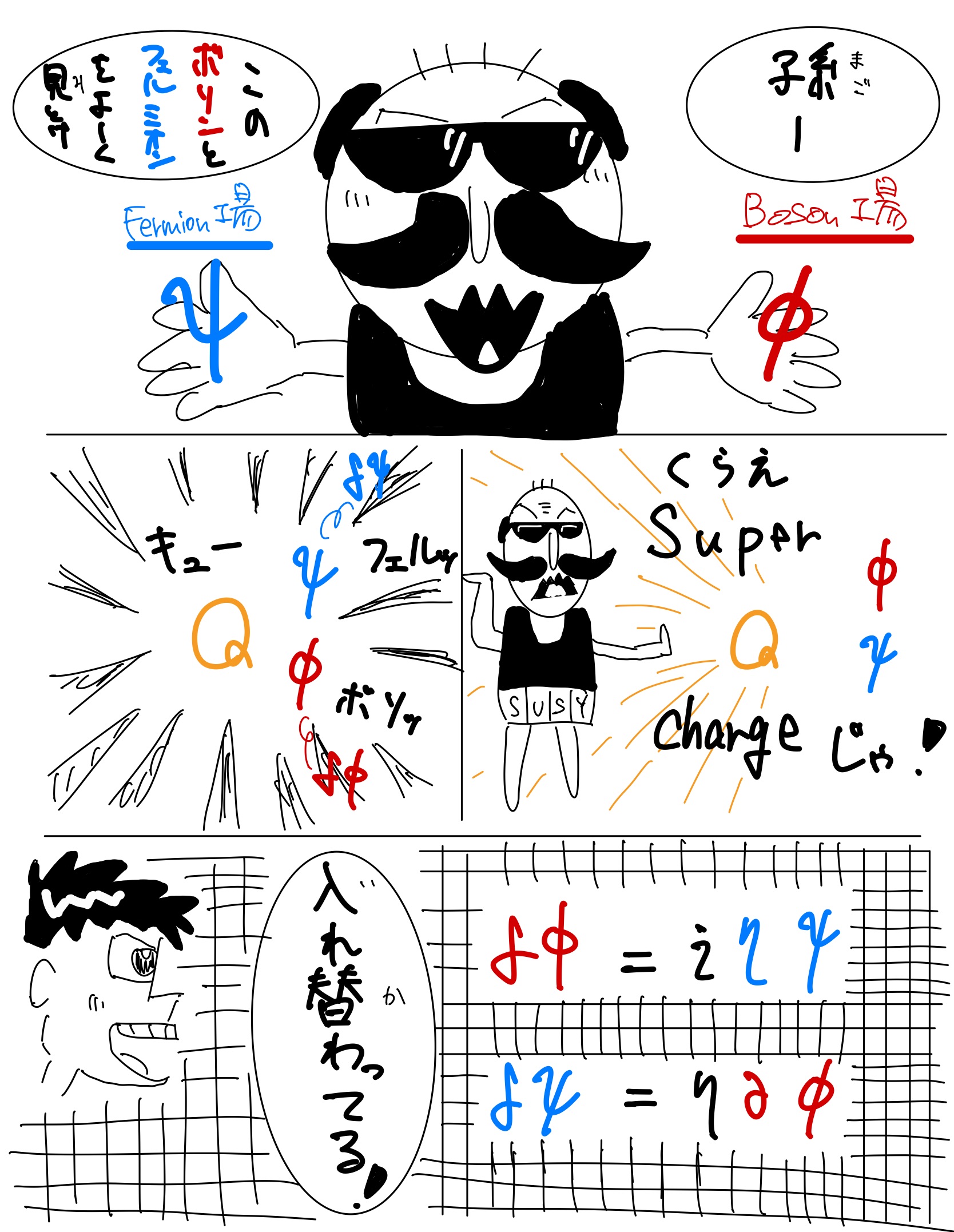
$\{\hat{Q}_\alpha,\hat{\bar{B}}_\dot{\beta}\} = 2\sigma ^{\mu} _{\alpha\dot{\beta}}\hat{P}_{\mu}$

この$\hat{Q}$こそが超対称演算子じゃ！！

孫）...

じ）この式をよくみると、左辺はスピノル添え字のスピノル量、右辺はベクトルの足がついたベクトル量となっておるんじゃ
つまり$\hat{Q}$がbosonとfermionを繋ぐ架け橋になっとるんじゃ

孫）そうなの？？
なんだかおじいちゃんの冗談にしか思えないのだけれど
運動量のルートなんてなんだか虚数みたいだね

じ）ふぉっふぉっふぉっ、こんな超対称演算子を用いることで虚数みたいな座標"Grassmann座標"が加わった超空間に行くことができるんじゃよ
実際に次の章ではこの超空間を散歩してみるかのぉ

※ちなみにHaag-Lopuszanski-Sohniusの定理と言うのがあってな、いつもの交換関係で定まる対称性に加え、反交換関係を許した上でColemann-Mandulaをどこまで拡張できるか考えるとこの超対称性しかないことが知られておるぞ!!

BosonとFermionが混ざるのじゃっ！

第二話

じ）微小変換がもとまったから有限変換の演算子に拡張するんじゃ
fermionicな座標（交換すると符号が変わるfermionicな数のことをGrassmann数とも言うんじゃ）への変換パラメタを$\theta^\alpha$のように置くと有限変換は
$G(x,\theta) \coloneqq \exp{(-ix^\mu\hat{P}_\mu + \theta^\alpha \hat{Q}_\alpha) }$
のようになるはずじゃ
と言われても抽象的でいまいちピンとこんのじゃ

ここからは具体的にどんな形をしているか見てみるんじゃ
$G(\varepsilon, \eta)G(x,\theta)=\exp({-i\varepsilon^a P_a+\eta^{\alpha}Q_{\alpha}})\exp({-ix^aP_a+\theta^\alpha Q_\alpha})$
これをBCH公式を用いて展開すると高次項が落ちてくれて
$\exp{\{-i(x^a+\varepsilon^a)P_a + (\theta^\alpha+\eta^\alpha)Q_\alpha\ + \frac{1}{2}[\eta Q, \theta Q]\} } $
のようになるんじゃ
fermionicな変換パラメタを括ろうとすると一回交換するから符号が変わるんじゃ！
そのおかげで最後の項は$\hat{Q}$の反交換関係になるぞ
だから最終的にはこんな形になるんじゃ！
$ G(\varepsilon, \eta)G(x,\theta) = \exp{\{-i(x^a + \varepsilon^a + \eta^\alpha \theta^\beta \sigma_{\alpha \beta}^a)P_a + (\theta ^{\alpha}+\eta ^\alpha)Q_\alpha\}}$
つまり$G(\varepsilon, \eta)$による微小変換は
$$ \begin{eqnarray} \left\{ \begin{array}{l} \delta x = \varepsilon + i\eta\theta \\ \delta \theta = \eta \end{array} \right. \end{eqnarray} $$
のようになるんじゃ
微小変換の作用の仕方がわかったから演算子の形で書きなおすこともできるんじゃ
$$ \begin{eqnarray} \left\{ \begin{array}{l} [P,\Phi] = -(-i\frac{\partial}{\partial x})\Phi\\ [Q, \Phi] = -(-\frac{\partial}{\partial \theta} + i\theta \frac{\partial}{\partial x})\Phi \end{array} \right. \end{eqnarray} $$

これが何を意味しているかは以下のようになるんじゃ

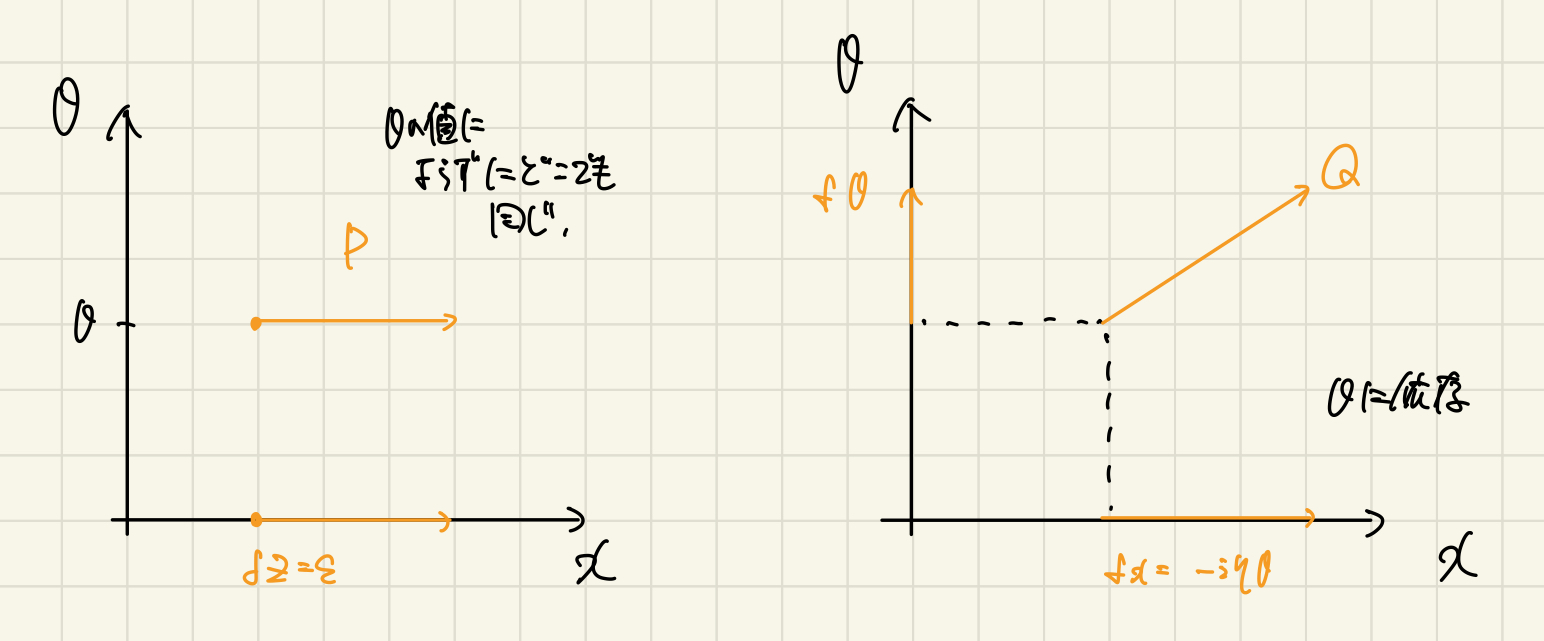運動量と超対称演算子

いつもの運動量は実空間で閉じているけど、超対称演算子は超空間方向への並進も引き起こすんじゃ！
これが後にbosonとfermionを混ぜることに対応するんじゃ

また、この超空間上に住むboson場、超場$\Phi(x,\theta)$を考えてみることもできるじゃろ
これをfermionicな座標$\theta$でTaylor展開してみるんじゃ
するとgrassmann数の冪ゼロ性$\theta^2=0$からこんな感じにBosonとFermionが出てきてくれるんじゃ〜

$ \Phi(x ,\theta, \bar{\theta}) = \phi(x) + i\{\theta \psi(x) + \bar{\theta}\bar{\psi}(x)\}+\theta \bar{\theta}F(x)$
但し$\phi,F$はboson場、$\psi$はfermion場じゃ
この時の$\phi$と$\psi$は超対称パートナー（Superpartner）と呼ばれるペアなんじゃ！
このように超対称性を導入するとbosonにはfermionの、fermionにはbosonの新しい粒子が予言されるんじゃ
例えば標準模型の粒子だと
・電子electronにはselectron
・光子photonにはphotino
みたいにbosonにはfermionっぽさを出すためneutrinoのお尻を取って-ino、fermionにはスカラーのs-を基本的にはつけることになっているんじゃ

孫）（スピノルだってs-じゃね...!?）

じ）変な名前じゃの
こんな感じに超対称性を入れると粒子の数が一気に増えるんじゃ〜

孫）なるほどね
そう言えばbosonとfermionが混ざるって言ってたね
それはどうやって見えるの？

じ）この超場を見るとわかりやすいんじゃの
超対称変換の微小変換を計算してみるんじゃ
微小変換は保存チャージとの交換関係だったんじゃな
$\delta_{\eta}\Phi = [\eta Q, \Phi]$
これを具体的に計算すると
$\eta(\frac{\partial}{\partial \theta}-i\theta \frac{\partial}{\partial x})(\phi+i\theta\psi+i\bar{\theta}\bar{\psi}+\theta\bar{\theta}F)=\eta[(i\psi)+i\theta(-\partial \phi)+i\bar{\theta}(-iF)+\theta\bar{\theta}(\partial \bar{\phi})]$
のようになるじゃろ
各項の変化分を見ると
$\delta_{\eta}\phi=i\eta\psi, \delta_\eta\psi = \eta\partial\phi, \delta _\eta \bar{\psi}=i\eta F, \delta _\eta F = \eta \partial \bar{\psi}$
のようになるのがわかるじゃろ
（$\theta$と$\eta$も反可換なことに注意なのじゃ！賢明な読者が指摘してくれたんじゃ）
このことから超対称変換をするとbosonにfermionの成分が、fermionにbosonの成分が混ざるのがわかるじゃろ！
これがbosonとfermionを混ぜる対称性という意味じゃ！

孫）そういう意味だったんだね
納得だよ！

じ）なんだか式もややこしくなってきたが大目にみてほしいんじゃ
ここからがとっても綺麗なんじゃぞ〜

※この章は数式のところにちょっぴりごまかしがあるんじゃ
もうボケかけのじーさんなんだと思って大目に見て欲しいんじゃ
アイデアは変わらんのじゃが、実際に式を追ってみたい人は 日本語ならこれ 、 英語ならこれ がおすすめなんじゃ

全ての力が統一するのじゃっ！

第三話

じ）孫よ この論文 の図2を見てみるんじゃ

論文のFig.2参照じゃ
これは標準模型に入っているgauge理論の結合定数のくりこみ群のflowを見た時に、どのような振る舞いをするかを標準模型+実験結果から予測したものなんじゃ
今の観測データから標準模型を使って計算するとどうやら高エネルギーに行くと、それぞれの結合定数がどうも一点で交わりそうな気がしてくるんじゃ

孫）交わると何が起こるの？

じ）標準模型では$U(1)\times SU(2)\times SU(3)$とバラバラだったgauge群がそれらを部分群に持つ一つの大きなgauge群（SU(5)など）に統一される大統一理論を示唆するんじゃ

孫）何それ！めちゃくちゃアツいじゃん！

じ）そうじゃろ〜激アツなんじゃ🤩

孫）でも標準模型では一致しないんでしょ
ならそんなことは起こらないってことなの？

じ）そこでSUSYなんじゃ！
孫よこのグラフを目に焼き付けるがよい

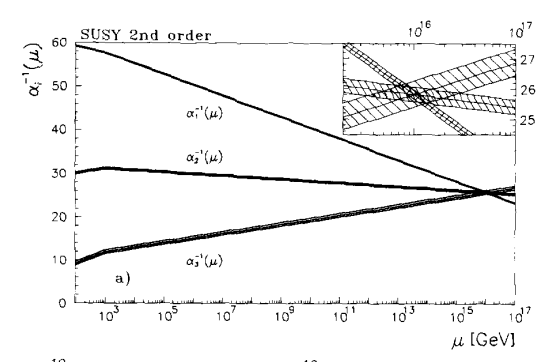論文のFig.2参照じゃ

じ）これはSUSYを入れた時に同様の計算をしたものなんじゃ！
だいたい$10^{16}$GeVあたりのところでそれぞれの結合定数が一点で交わるんじゃ！
大したもんじゃろ！

孫）すごい！！超対称性はあります！！

じ）ちなみにこのことから線が交わる$ 10^{16}$GeVぐらいがGUTスケールと呼ばれていて、このぐらいの高エネルギーの物理を見れば統一理論が現れることが期待されているんじゃ

孫）でも$10^{16}$GeVってめちゃくちゃ大きなエネルギースケールだよね
確かあんなに頑張って最近見つけたHiggsが100GeVぐらいだし...
こんなのどうやって検証するの？

じ）その一つに我らが日本のカミオカンデによる実験があるぞ！

標準模型ではleptonとquarkはSU(3)の異なる表現（シングレット、トリプレット）だったんじゃ
異なる表現の粒子同士は相互作用の入り方が違うからお互いに混ざり合わないんじゃ

しかし、三つのgauge群が一つの大きなgauge群に統一された大統一理論 略してGUT（Grand Unified Theory）では、lepton,quarkが同じ表現に入ることでそれらが混ざり合うんじゃ
このことから標準模型では安定で崩壊先のなかったleptonの陽子が、陽電子と$\pi$中間子(合体したquark)に崩壊するいわゆる陽子崩壊が予言されるんじゃ

一般にエネルギースケールが離れるほど、その物理は起こりにくくなるんじゃ
起こる確率はとっても低くても、大量にイベントを用意して、長い時間待てば高エネルギーの現象も確率的には観測にかかるはずじゃ

これを水分子をいっぱい貯めて、その陽子が崩壊するのをじっっっと待っておるのが日本のカミオカンデじゃ
（今じゃすっかりニュートリノで有名じゃが実はカミオカンデのンデは核子崩壊実験 Nucleon Decay Experimentに由来しとるんじゃぞ）
いつか陽子崩壊が見れた暁には世界中が大騒ぎじゃ

孫）カミオカンデってそんなこともしてたんだ！
夢があってワクワクするね

時空が10次元になるのじゃっ！

第四話

じ）孫は電磁場のゲージ固定とかしたことあるかのぉ

孫）電磁気の授業でちょっとだけやったよ！

じ）ならよろしい
せっかくだから弦理論と超対称性を合わせてでてくる面白い現象を紹介してやるのじゃ

あの時ゲージ固定によって進行方向の縦波が禁止され、4次元時空から時間と縦波方向の2自由度を引いた$4-2=2$自由度がゲージ場の自由度になってたのを覚えてるかのぉ

孫）確かにあったかも！重力波でも同じようなことを計算したことを思い出した！

じ）誰に似たのか勘が鋭いのぉ
おんなじようなことが一般の次元でも成り立つんじゃ
さらに実はゲージ場に限らずmasslessだったらみんなそうじゃ（ウィグナーの分類とかを調べてみるんじゃの）
だから一般にmassless粒子の自由度は$D-2$あるはずじゃ

次にこの時の調和振動子の零点エネルギーを計算してみるんじゃ
調和振動子の生成消滅演算子はboson,fermionでそれぞれ
$[a^{\dagger},a]=1, \{c^{\dagger}, c\}=1$
のようになっていたのを覚えているかのぉ
弦理論では今まで点だった1次元の粒子を一つ次元の高い2次元のヒモだと考える理論なんじゃ
だからそれぞれ粒子が内部自由度として振動モードを持っておるぞ

調和振動子と同じように、その振動モードの生成消滅演算子が定義できて
$[\alpha_n, \alpha_{-n}]=n$
の交換関係を満たすんじゃ
いつもの交換関係とモードの値$n$の分だけ違うことに注意するんじゃ
各モードごとに異なる調和振動子がたくさん置いてあるのが弦理論じゃの
これでbosonだけの弦理論の作用を書き換えると真空エネルギーである定数部分が

$(D-2)\times \sum_{n=1}^\infty \frac{n}{2}=\frac{D-2}{2}\zeta (-1)$

のようになるんじゃ
このnに関する無限和は$\zeta$関数の正則化により$\zeta (-1)-\frac{1}{12}$になることが知られてるんじゃ

こいつに超対称性を持たせると、さっき見たようにbosonとfermionがペアで現れるから同時にfermionのモードも生じるんじゃ
その時には交換関係の符号が異なるおかげでbosonとは真空エネルギーが反対符号になるんじゃ！

いかんいかん話を戻すのじゃ
これについては後でもう少しだけ触れるんじゃ

fermionの場合は今度は反対符号でさらに境界条件から$\frac{1}{2}$ずれて
$-(D-2)\sum_{n=0}^{\infty}(n + \frac{1}{2})$
になるんじゃ

またこれに数学者から聞いたおまじない"解析接続"を使ってやると$\sum_{n=0}^{\infty}(n + \frac{1}{2}) = \frac{1}{24}$と計算でき
$-\frac{D-2}{48}$
となるんじゃ

話をまとめると、この弦の真空エネルギーは
$-\frac{D-2}{24}-\frac{D-2}{48} = -\frac{D-2}{16}$
になることがわかるんじゃ

続いて、この理論の一番軽い粒子である第一励起状態を見てやるんじゃ
それは真空にfermionの生成演算子を作用させてエネルギーを$\frac{1}{2}$上げた状態じゃな
こいつの質量はどうなるかわかるか、孫？

孫）えっと、さっきの真空エネルギーにこの$\frac{1}{2}$を足してあげればいいのかな？

じ）大正解じゃ！
さすがわしの孫じゃの！
この粒子の物理的な意味を考えてみるんじゃ
今は横波自由度しかないmassless粒子を考えていたんじゃったな
質量を持つと対称性が変わって$D-2$自由度じゃ無くなっちゃうんじゃ

このことから質量が$0$になることが要請されるんじゃ

孫）なるほど！
つまり
$\frac{1}{2}-\frac{D-2}{16}=0$
が成り立つってとね
確かにこれを解くと$D=10$と時空が10次元になった！
本当に時空が10次元にならないと、つじつまが合わなくなっちゃうということなんだね！

じ）そうなんじゃ
これが超対称性を持つ弦理論により時空が10次元であることが予言されることの説明の一つなんじゃ
めでたしめでたしじゃの

孫）理論的な制約から時空の次元まで決定しちゃうなんて、、理論物理って面白いね！
でも10次元なんてまるでギャグ漫画の世界だよ！！

見つからないんじゃっ！

第五話

じ）孫はくりこみの計算はしたことあるかのぉ

孫）Peskinの計算をちょっと追ってみたことはあるよ

じ）ならバッチリじゃの
質量を計算するときに裸の質量に相殺項を足して観測値と合わせるじゃろ
例えばHiggs粒子などの標準模型の粒子は100GeVぐらいの質量じゃが、標準模型が有効なカットオフスケール例えばPlanckスケールは$10^{19}$ GeVくらいじゃ
くりこみの計算をするときに、そのカットオフスケールの二乗に比例する項が1次で入ってきて、それを相殺項で取り除いたのを覚えておるか？
じゃから相殺項として$10^{30}$ぐらい異なる量を引き算して$10^4$ぐらいの量を残さなきゃいかんのじゃ
それってなんだか不自然じゃろ
でもSUSYが入るとこの不自然な項は反対符号を持ったペアが生じて勝手に消えてくれるんじゃ！

孫）確かにそれなら自然な気がするし、とっても綺麗だね！

じ）もちろん現実はSUSYのスケールに比べてずっと低エネルギーで超対称性は破れてると考えられとるんじゃ
でもその破れ方によって超対称パートナーの質量が何かしらの影響を受けるはずなんじゃな
一番観測しやすいのがHiggsの超対称パートナーとされているんじゃがその質量は1~10TeVぐらいが標準模型とSUSYのエネルギースケールの乖離の観点から自然だと考えられているんじゃ

孫）1TeVくらいならギリギリ実験で見れそうじゃん！

じ）そうなんじゃ
でもな、Higgsを発見したCERNでそれくらいのエネルギーを探索できるんじゃが、ことごとく見つからないんじゃ
SUSYが禁止された訳ではないんじゃが、どんどん立場が怪しくなっているのが現状じゃ

孫）あんなに綺麗で面白い結果があるのに、現実を見てみると全然見つからないって不思議だね
ますます気になるよ！

終わりに

最後まで読んでくれてありがとうなのじゃ

ここまで読んだと言うことはよっぽど物理が好きか、よっぽど暇だったかのどっちかじゃな

クリスマスに暇っちゅうのはなんとも寂しいもんじゃが、この記事を読むことで少しでもその寂しさを和らぐことができたならワシとしては本望なんじゃ
そんなお主に来年までにはSuperなPartnerが見つかるようにワシも祈っておるぞ
（きっととってもエネルギーが必要じゃがの）

それではもうお別れじゃ
また会う日まで達者でな〜
あらためてMerry Christmasなのじゃ〜