【自作問題】数学A・組み合わせの練習
まえがき
こんにちは、高3のぱぺです。
本編の前にちょっと雑談をしましょう。飛ばしても構いません。
雑談部分。(実はこういう「アコーディオン機能」を使いたいがためにやっているのが大きい。)
最近母が『薬屋のひとりごと』のアニメを観るのに夢中で、ちょくちょく私も見るんですが、
最近ようやく$2$期が終わりましたね。$47$話は泣かせにきてるだろおい。
YouTubeで薬屋のひとりごとのCVさんたちがお話ししていたりするのを見るのもまたいいものですね。
それから睡蓮さま、最初聞いたとき絶対ワイズマン博士(『おさるのジョージ』)だろって思いました。CV同じ人でした。
本題
今回は数学Aの組み合わせの問題を$4$題出します。
一部問題演習に使えるかと思います。第$4$問はお気に入りの(自信作の)自作問題なので、得意な方はぜひ挑戦してみてください。
解答はまえがきのようにアコーディオン機能を用います。
問題1 (6/22作問)
図のように、一辺$1$の正三角形$2$つと正方形$1$つを図$1$のように組み合わせて図形$D_1$をつくる。このとき$D_1$は$6$頂点をもつ。
$n$を自然数とする。$n$個の$D_1$を図$2$のように横に連結させ、図形$D_n$をつくる。このとき$D_n$は$4n+2$個の頂点をもつ。
以下の問いに答えよ。
![図!FORMULA[18][65514038][0], 図!FORMULA[19][953076340][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fm3x35Tu3NQE2M6XCNCWf.png?alt=media) 図$1(D_1)$, 図$2(D_n)$
図$1(D_1)$, 図$2(D_n)$
$\text{(1)}$ $D_1$の$6$頂点を黒と白のちょうど$2$色で塗り分ける。こうしてできる図形は何種類できるか。
ただし、反転・回転をして一致するものは同じ塗り分け方、すべての白と黒を逆転したものは異なる塗り分け方とみなす。
$\text{(2)}$ $D_n$の$4n+2$個の頂点を黒と白のちょうど$2$色で塗り分ける。こうしてできる図形は何種類できるか。$n$を用いて表せ。
ただし、反転・回転をして一致するものは同じ塗り分け方、すべての白と黒を逆転したものは異なる塗り分け方とみなす。
$ $
以下解答です。
$\text{(1)}$ 解答(答えのみ)
$\text{(1)}$ $22$種類
$\text{(1)}$ 解説
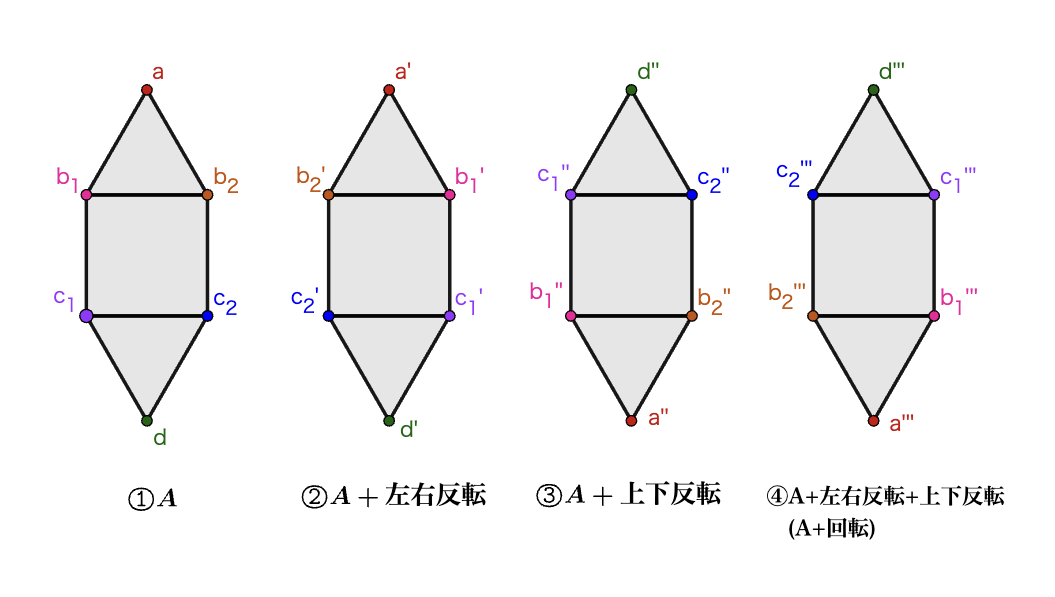 回転・反転による図形の一致
回転・反転による図形の一致
$\text{(1)}$ 上図の$①$~$④$で、$6$頂点$a,b_1,b_2,c_1,c_2,d$をそれぞれ同じ色で塗った際、これらの塗り方はすべて同じ塗り方とみなされるが、これらを区別するため便宜的に、反転や回転をして同じになるものを区別したときの塗り方を「塗られ方」と呼ぶことにする。
図形$D_1$を黒と白のちょうど$2$色で塗り分ける際の塗られ方の総数は$2^6-2=62$通り。
これらの塗られ方は
$\text{A : }$ 左右対称であり、上下対称でないもの
$\text{B : }$ 上下対称であり、左右対称でないもの
$\text{C : }$ 点対称であり、左右・上下対称ではないもの
$\text{D : }$ 左右対称であり、上下対称であるもの
$\text{E : }$ 左右・上下対称でなく、点対称でもないもの
の$5$種類に分類される。回転・反転により一致するものは、$1$組の一致につきそれぞれ
$\text{A : }$ $①=② \neq ③=④$ で$2$通り
$\text{B : }$ $①=③ \neq ②=④$ で$2$通り
$\text{C : }$ $①=④ \neq ②=③$ で$2$通り
$\text{D : }$ $①=②=③=④$ で$1$通り
$\text{E : }$ $①\neq② \neq ③\neq④$ で$4$通り
であるため、分類$P$に分類される塗られ方の総数を$n(P)$とおくと、求める塗り方の総数$N_1$は
$$N_1=\frac{1}{2} \left\{ n(A)+n(B)+n(C) \right\}+n(D)+\frac{1}{4}n(E) \; \text{ 通り}$$
$ $
$ $
・左右対称である塗られ方の総数は $n(A)+n(D)$である。
塗られ方として対称軸上の$2$頂点とそれより右側の$2$頂点,計$4$頂点の色が決まればよい。
$2^4-2=14$通りより、 $n(A)+n(D)=14 -[1]$
・上下対称である塗られ方の総数は $n(B)+n(D)$である。
塗られ方として対称軸より上側の$3$頂点の色が決まればよい。
$2^3-2=6$通りより、 $n(B)+n(D)=6 -[2]$
・点対称である塗られ方の総数は $n(C)+n(D)$である。
塗られ方として対称の中心より上側の$3$頂点の色が決まればよい。
$2^3-2=6$通りより、 $n(C)+n(D)=6 -[3]$
・左右対称かつ上下対称である塗られ方の総数は $n(D)$ 通りである。
塗られ方として、正方形の$4$頂点と上下端の$2$頂点がそれぞれ同じ色であればよい。
$2^2-2=2$通りより、$n(D)=2 -[4]$
・塗られ方の総数は$62$通りより、 $n(A)+n(B)+n(C)+n(D)+n(E)=62 -[5]$
したがって、
\begin{aligned} N_1&=\frac{1}{2} \left\{ n(A)+n(B)+n(C) \right\}+n(D)+\frac{1}{4}n(E) \\ &=\frac{n(A)+n(B)+n(C)+n(D)+n(E)}{4}+\frac{n(A)+n(D)}{4}+\frac{n(B)+n(D)}{4}+\frac{n(C)+n(D)}{4}\\ &=\frac{62}{4}+\frac{14}{4}+\frac{6}{4}+\frac{6}{4} \; \left[ \;\because [1],[2],[3],[5] \; \right] \\ &=22 \end{aligned}
以上から、求める塗り方の総数は$\textbf{22}$通りである。
$\text{(2)}$ 解答(答えのみ)
$\text{(2)}$ $2^{4n}+2^{2n+1}-2$種類
$\text{(2)}$ 解説
$\text{(2)}$ 図形$D_1$を黒と白のちょうど$2$色で塗り分ける際の塗られ方の総数は$2^{4n+2}-2$通り。
これらの塗られ方は
$\text{A : }$ 左右対称であり、上下対称でないもの
$\text{B : }$ 上下対称であり、左右対称でないもの
$\text{C : }$ 点対称であり、左右・上下対称ではないもの
$\text{D : }$ 左右対称であり、上下対称であるもの
$\text{E : }$ 左右・上下対称でなく、点対称でもないもの
の$5$種類に分類される。回転・反転により一致するものは、$1$組の一致につきそれぞれ(1)の$①$~$④$を用いると
$\text{A : }$ $①=② \neq ③=④$ で$2$通り
$\text{B : }$ $①=③ \neq ②=④$ で$2$通り
$\text{C : }$ $①=④ \neq ②=③$ で$2$通り
$\text{D : }$ $①=②=③=④$ で$1$通り
$\text{E : }$ $①\neq② \neq ③\neq④$ で$4$通り
であるため、分類$P$に分類される塗られ方の総数を$n(P)$とおくと、求める塗り方の総数$N_n$は
$$N_n=\frac{1}{2} \left\{ n(A)+n(B)+n(C) \right\}+n(D)+\frac{1}{4}n(E) \; \text{ 通り}$$
$ $
$ $
$\text{(I)}$ $n$が奇数のとき
![例:!FORMULA[133][36584066][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FcNPweq4m64sbZfdWZpYU.png?alt=media) 例:$n=5$
例:$n=5$
・左右対称である塗られ方の総数は $n(A)+n(D)$である。
塗られ方として対称軸上の$2$頂点とそれより右側の$2n$頂点,計$2n+2$頂点の色が決まればよい。
$2^{2n+2}-2$通りより、 $n(A)+n(D)=2^{2n+2}-2 -[1.1]$
・上下対称である塗られ方の総数は $n(B)+n(D)$である。
塗られ方として対称軸より上側の$2n+1$頂点の色が決まればよい。
$2^{2n+1}-2$通りより、 $n(B)+n(D)=2^{2n+1}-2 -[1.2]$
・点対称である塗られ方の総数は $n(C)+n(D)$である。
塗られ方として対称の中心より上側の$2n+1$頂点の色が決まればよい。
$2^{2n+1}-2$通りより、 $n(C)+n(D)=2^{2n+1}-2 -[1.3]$
・左右対称かつ上下対称である塗られ方の総数は $n(D)$ 通りである。
塗られ方として左右対称軸上またはそれより右側にあり、上下対称軸より上側にある計$n+1$頂点の色が決まればよい。
$2^{n+1}-2=2$通りより、$n(D)=2^{n+1}-2 -[1.4]$
・塗られ方の総数は$2^{4n+2}-2$通りより、 $n(A)+n(B)+n(C)+n(D)+n(E)=2^{4n+2}-2 -[1.5]$
したがって、
\begin{aligned} N_n&=\frac{1}{2} \left\{ n(A)+n(B)+n(C) \right\}+n(D)+\frac{1}{4}n(E) \\ &=\frac{n(A)+n(B)+n(C)+n(D)+n(E)}{4}+\frac{n(A)+n(D)}{4}+\frac{n(B)+n(D)}{4}+\frac{n(C)+n(D)}{4}\\ &=\frac{2^{4n+2}-2}{4}+\frac{2^{2n+2}-2}{4}+\frac{2^{2n+1}-2}{4}+\frac{2^{2n+1}-2}{4} \; \left[ \;\because [1.1],[1.2],[1.3],[1.5] \; \right] \\ &=2^{4n}+2^{2n+1}-2 \end{aligned}
$\text{(II)}$ $n$が偶数のとき
 例:n=4
例:n=4
・左右対称である塗られ方の総数は $n(A)+n(D)$である。
塗られ方として対称軸上の$2$頂点とそれより右側の$2n$頂点,計$2n+2$頂点の色が決まればよい。
$2^{2n+2}-2$通りより、 $n(A)+n(D)=2^{2n+2}-2 -[2.1]$
・上下対称である塗られ方の総数は $n(B)+n(D)$である。
塗られ方として対称軸より上側の$2n+1$頂点の色が決まればよい。
$2^{2n+1}-2$通りより、 $n(B)+n(D)=2^{2n+1}-2 -[2.2]$
・点対称である塗られ方の総数は $n(C)+n(D)$である。
塗られ方として対称の中心より上側の$2n+1$頂点の色が決まればよい。
$2^{2n+1}-2$通りより、 $n(C)+n(D)=2^{2n+1}-2 -[2.3]$
・左右対称かつ上下対称である塗られ方の総数は $n(D)$ 通りである。
塗られ方として左右対称軸上またはそれより右側にあり、上下対称軸より上側にある計$n+1$頂点の色が決まればよい。
$2^{n+1}-2=2$通りより、$n(D)=2^{n+1}-2 -[2.4]$
・塗られ方の総数は$2^{4n+2}-2$通りより、 $n(A)+n(B)+n(C)+n(D)+n(E)=2^{4n+2}-2 -[2.5]$
したがって、
\begin{aligned} N_n&=\frac{1}{2} \left\{ n(A)+n(B)+n(C) \right\}+n(D)+\frac{1}{4}n(E) \\ &=\frac{n(A)+n(B)+n(C)+n(D)+n(E)}{4}+\frac{n(A)+n(D)}{4}+\frac{n(B)+n(D)}{4}+\frac{n(C)+n(D)}{4}\\ &=\frac{2^{4n+2}-2}{4}+\frac{2^{2n+2}-2}{4}+\frac{2^{2n+1}-2}{4}+\frac{2^{2n+1}-2}{4} \; \left[ \;\because [2.1],[2.2],[2.3],[2.5] \; \right] \\ &=2^{4n}+2^{2n+1}-2 \end{aligned}
$\text{(I)(II)}$から、求める塗り方の総数は$\mathbf{2^{4n}+2^{2n+1}-2}$通りである。
$ $
$ $
問題2 (7/9作問)
$A,B,C$をそれぞれ1以上$n$以下の自然数とする。
$f(1)=A, \; f(0)=B, \; f(-1)=C$ を満たすような$2$次以下の$x$の整式$f(x)$を考える。
ここで、$f(x)$が整数係数の$x$の$2$次式であるような$(A,B,C)$の組の個数を$N(n)$とする。
実数$x$に対して、$x$を超えない最大の整数を$\displaystyle \left[x\right]$と表すとして、以下の問いに答えよ。
$\text{(1)} \hspace{1em}$ $\displaystyle I=\left[\frac{n+1}{2}\right]$ とおくとき、$N(n)$を$n,I$を用いて表せ。
$\text{(2)} \hspace{1em}$ 極限$\displaystyle \lim_{n\rightarrow ∞} \frac{N(n)}{n^3}$ を求めよ。
$ $
以下解答です。
$\text{(1)}$ 解答(答えのみ)
$N(n)=(n-1)\left\{I^2+(n-I)^2\right\}$
※ $\displaystyle I=\frac{n+1}{2},\frac{n}{2}$であるから、$\left\{2I-(n+1)\right\}\left(2I-n\right)=0$
これを展開して $4I^2-2(2n+1)I+n^2+n=0$ より、解答に関しては
$$N(n)=(n-1)\left\{I^2+(n-I)^2\right\}+P(n)\left\{4I^2-2(2n+1)I+n^2+n\right\}$$
の形であるものも正答とします。つまり
$\displaystyle N(n)=\frac{1}{2} \left(n^2+2I-n\right)(n-1) \qquad \left[ \; P(n)= -\frac{1}{2}(n-1) \; \right]$
などの形も可です。
$ $
$\text{(1)}$ 解説
$f(x)=ax^2+bx+c$とおくと、$A=a+b+c, \; B=c, \ C=a-b+c$ と表されるから、
$\displaystyle a=\frac{A+C}{2}-B, \; b=\frac{A-C}{2}, \; c=B$
$a=b+C-B$より、$b$が整数ならば、$a$も整数となる。
また、$B$は整数であるから$c$は常に整数となる。
従って、題意を満たすような$(A,B,C)$の条件は、「$b$が整数かつ$A\neq 0$」である。
$ $
$b$が整数となるような組み合わせを考えると、$b$が整数となるのは$A,C$の偶奇が等しいときであるから、
$A,C$がともに奇数、またはともに偶数であるような$(A,C)$の組を考える。
$1$以上$n$以下の整数のうち奇数は$\displaystyle \left[\frac{n+1}{2}\right]=I$個、偶数は$n-I$個であるから、
$A,C$がともに奇数となるのは$I^2$通り、
$A,C$がともに偶数となるのは$(n-I)^2$通り。
したがって、$(A,C)$の組は$I^2+(n-I)^2$個。
$ $
ここで、各$(A,C)$の組に対して、条件を満たすような$B$が何個あるかを考える。
$B$が取りうる値は$1$以上$n$以下の$n$個の整数である。
このうち$a=0$であるような$B$の値を全て求める。
$\displaystyle a=0 \Leftrightarrow B=\frac{A+C}{2}$であり、$A$と$C$の偶奇は等しく$\displaystyle \frac{A+C}{2}$は$1$以上$n$以下の整数値を取るため、$a=0$を満たすような$B$は常に$1$つだけ存在する。
従って、条件を満たす$b$は各$(A,C)$の組に対しちょうど$n-1$個だけ存在する。
$ $
以上から、求める$(A,B,C)$の組の個数は$N(n)=(n-1)\left\{I^2+(n-I)^2\right\}$ 個ある。
$ $
$\text{(2)}$ 解答(答えのみ)
$\displaystyle \lim_{n\rightarrow ∞} \frac{N(n)}{n^3}=\frac{1}{2}$
$\text{(2)}$ 解説
$\displaystyle \frac{n-1}{2}<\left[\frac{n+1}{2}\right] \leq \frac{n+1}{2}$ かつ、$\displaystyle \lim_{n\rightarrow ∞} \frac{1}{n}\cdot \frac{n-1}{2}=\lim_{n\rightarrow ∞} \frac{1}{n}\cdot \frac{n+1}{2}=\frac{1}{2}$であるから、
はさみうちの原理より $\displaystyle \lim_{n\rightarrow ∞} \frac{I}{n}=\frac{1}{2}$
したがって、
\begin{aligned} \lim_{n\rightarrow ∞} \frac{N(n)}{n^3} &=\lim_{n\rightarrow ∞} \frac{(n-1)\left\{I^2+(n-I)^2\right\}}{n^3} \\ &=\lim_{n\rightarrow ∞} \left(1-\frac{1}{n}\right)\left\{\left(\frac{I}{n}\right)^2+\left(1-\frac{I}{n}\right)^2\right\} \\ &=(1-0)\left\{\left(\frac{1}{2}\right)^2+\left(1-\frac{1}{2}\right)^2\right\} \\ &=\frac{1}{2} \end{aligned}
$ $
$ $
$ $
問題3 (7/13作問)
$\text{H,I,G,H,S,C,H,O,O,L}$の$10$文字を並べ替えて文字列をつくる。次の条件を満たすものはそれぞれ何種類あるか。
$\text{(1)}$ $\text{S}$で始まり$\text{L}$で終わる
$\text{(2)}$ $\text{H}$が$2$文字だけ連続するが、$\text{O}$どうしは連続しない
$\text{(3)}$ 同じ文字が連続しない
$\text{(4)}$ 文字列$\text{HO}$を$1$つだけ含み、そのどちらの隣にも$\text{H}$や$\text{O}$は位置しない(ただし$\text{HO}$は端にあってもよい。)
$ $
以下解答です。
$\text{(1)}$ 解答(答えのみ)
$ 3360 $種類
$ $
$\text{(1)}$ 解説
$1$文字目が$\text{S}$, $10$文字目が$\text{L}$である文字列について、$2$〜$9$文字目に入るのは$\text{C,G,H,H,H,I,O,O}$ の$8$文字であるから、その種数は$ \displaystyle \frac{8!}{3! 2!}=3360 $通り
$ $
$\text{(2)}$ 解答(答えのみ)
$22\cdot 7!=110880$種類
$ $
$\text{(2)}$ 解説
$\text{HH}$を$\text{[A]}$とおく。
$\text{[A],H}$が隣り合わず、文字列$\text{OO}$を含まないものを考える。
文字列$\text{HH}$を含み、文字列$\text{OO}$を含まないものの総数について、
$\text{(}$ $\text{[A],C,G,H,I,L,O,O,S}$の$9$個を並び替えた総数$\text{)} - \text{(}$ $\text{[A],C,G,H,I,L,OO,S}$の$8$個を並び替えた総数$\text{)}$であるから、
$\displaystyle \frac{9!}{2!}-8!=28 \cdot 7!$ 通り。
文字列$\text{[A]H or H[A]}$を含み文字列$\text{OO}$を含まないものの総数について、
$\text{H,[A]}$を合わせたものを$\text{[B]}$とおくと、
$\text{[B]}$について$\text{[A],H}$の並べ方は$2!$通りであり、
$\text{[ (}$ $\text{[B],C,G,I,L,O,O,S}$の$8$個を並び替えた総数$\text{)} - \text{(}$ $\text{[B],C,G,I,L,OO,S}$の$7$個を並び替えた総数$\text{) ]} \times 2!$であるから
$\displaystyle \left\{ \frac{8!}{2!}-7! \right\} \cdot 2! =6 \cdot 7!$ 通り。
したがって、求める並べ方の総数は
$28\cdot 7! - 6 \cdot 7! =22\cdot 7!=110880$通り
$ $
$\text{(3)}$ 解答(答えのみ)
$23\cdot 7! =115920$種類
$ $
$\text{(3)}$ 解説
求める並べ方の総数は
$\text{(}$ 文字列$\text{OO}$を含まないものの総数 $\text{)} - \text{(}$ $\text{H}$が$2$つだけ連続し、文字列$\text{OO}$を含まないものの総数$\text{)} - \text{(}$ 文字列$\text{HHH}$を含み、文字列$\text{OO}$を含まないものの総数 $\text{)}$
で表される。
$ $
文字列$\text{OO}$を含まないものの総数は
$\text{(}$ $\text{H,H,H,C,G,I,L,O,O,S}$の$10$個を並び替えた総数 $\text{)}- \text{(}$ $\text{H,H,H,C,G,I,L,OO,S}$の$9$個を並び替えた総数 $\text{)}$
で表されるから、$\displaystyle \frac{10!}{3!2!}-\frac{9!}{3!} = 48 \cdot 7!$ 通り。
$ $
文字列$\text{HHH}$を含み、文字列$\text{OO}$を含まないものの総数は
$\text{(}$ $\text{HHH,C,G,I,L,O,O,S}$の$8$個を並び替えた総数 $\text{)}- \text{(}$ $\text{HHH,C,G,I,L,OO,S}$の$7$個を並び替えた総数 $\text{)}$
で表されるから、$\displaystyle \frac{8!}{2!}-7! = 3 \cdot 7!$ 通り。
$ $
$\text{H}$が$2$つだけ連続し、文字列$\text{OO}$を含まないものの総数は$\text{(2)}$より$22\cdot 7!$通り
したがって、求める並べ方の総数は
$48\cdot 7! -22\cdot 7! -3\cdot 7!=23\cdot 7! =115920$通り
$ $
$\text{(4)}$ 解答(答えのみ)
$75\cdot6! =54000$種類
$ $
$\text{(4)}$ 解説
$1$個だけの文字である$C,G,I,L,S$からなる集合を$\mathbb{S}$とする。
以下、$\text{(I)(II)}$において、$\mathbb{S}$のある$1$つの要素を、$\mathbb{S}_1$と表すとする。
\begin{aligned} \mathbb{S}_2= \;&\text{C} \; (\; \text{if} \; \mathbb{S}_1=\text{G} \;), &\text{G} \; ( \; \text{otherwise} \; ) \\ \mathbb{S}_2= \;&\text{C} \; (\; \text{if} \; \mathbb{S}_1=\text{I} \;), &\text{I} \; ( \; \text{otherwise} \; ) \\ \mathbb{S}_2= \;&\text{C} \; (\; \text{if} \; \mathbb{S}_1=\text{L} \;), &\text{L} \; ( \; \text{otherwise} \; ) \\ \mathbb{S}_2= \;&\text{C} \; (\; \text{if} \; \mathbb{S}_1=\text{S} \;), &\text{S} \; ( \; \text{otherwise} \; ) \end{aligned}
であるとする。
$\text{HO}$がどの位置にくるかについて考える。
$\text{(I)}$ $\text{HO}$ が左端にくるとき
$\quad$ $\text{ H O ① | ・ ・ ・ ・ ・ ・ ・ } $
$\quad$ $①$に入るものは$\mathbb{S}_1$であり、$5$通り。
$\quad$ 残りの$7$つについて、$\text{H,H,O,} \mathbb{S_2},\mathbb{S_3},\mathbb{S_4},\mathbb{S_5}$を用いて$\text{HO}$を含まない並べ方を考える。
$\quad$ 単純に並べる方法の総数は $\displaystyle \frac{7!}{2!}= 21\cdot 5!$ 通り
$\quad$ うち$\text{HO}$を含む並べ方の総数は、$\text{H , HO , } \mathbb{S_2},\mathbb{S_3},\mathbb{S_4},\mathbb{S_5}$ を並べる方法であり、 $6!$通り
$\quad$ したがって、残り$7$枠で$\text{HO}$を含まない並べ方の総数は$21\cdot 5! -6!=15\cdot 5!$通りであるから、
$\quad$ $\text{HO}$が左端にくるのは$15\cdot 5! \times 5=75\cdot 5!$ 種類
$\text{(II)}$ $\text{HO}$ が右端にくるとき
$\quad$ $\text{ ・ ・ ・ ・ ・ ・ ・ | ① H O} $
$\quad$ $①$に入るものは$\mathbb{S}_1$であり、$5$通り。
$\quad$ 残りの$7$つについて、$\text{H,H,O,} \mathbb{S_2},\mathbb{S_3},\mathbb{S_4},\mathbb{S_5}$を用いて$\text{HO}$を含まない並べ方を考える。
$\quad$ 単純に並べる方法の総数は $\displaystyle \frac{7!}{2!}= 21\cdot 5!$ 通り
$\quad$ うち$\text{HO}$を含む並べ方の総数は、$\text{H , HO , } \mathbb{S_2},\mathbb{S_3},\mathbb{S_4},\mathbb{S_5}$ を並べる方法であり、 $6!$通り
$\quad$ したがって、残り$7$枠で$\text{HO}$を含まない並べ方の総数は$21\cdot 5! -6!=15\cdot 5!$通りであるから、
$\quad$ $\text{HO}$が右端にくるのは$15\cdot 5! \times 5=75\cdot 5!$種類
$\text{(III)}$ $\text{HO}$ が両端にこないとき
$\quad$ $\text{HO}$の両端にはともに$\mathbb{S}$の要素が位置するが、この$2$つの位置は区別されるため、
$\quad$ その位置の仕方は$_5\text{P}_2=20$通りであり、残った$\mathbb{S}$の$3$つの要素は、各場合で一意に決まる。
$\quad$ $\text{HO}$ とその両隣の$2$文字、合計$4$文字をまとめて$[C]$とおく。
$\quad$ $[C],\text{H,H,O}$と$\mathbb{S}$の$3$つの要素の合計$7$つを並べ替えて、$[C]$内の$\text{HO}$を除いて$\text{HO}$を含まない並べ方を考える。
$\quad$ 単純に並べる方法の総数は $\displaystyle \frac{7!}{2!}= 21\cdot 5!$ 通り
$\quad$ うち$\text{HO}$を含む並べ方の総数は、$[C], \text{H , HO , }$そして$ \mathbb{S}$の$3$要素 を並べる方法であり、 $6!$通り
$\quad$ したがって、$[C]$内の$\text{HO}$を除いて$\text{HO}$を含まないような並べ方の総数は$21\cdot 5! -6!=15\cdot 5!$通りであるから、
$\quad$ $\text{HO}$が中央にくる並べ方の総数は$15\cdot 5! \times 20=300\cdot 5!$種類
$ $
$\text{(I)(II)(III)}$より、求める並べ方の総数は
$75\cdot 5!+75\cdot 5!+300\cdot5!=450\cdot5!$
$(=75\cdot6!) =54000$種類
$ $
確認用Pythonコード
編集画面ではちゃんとインデントを揃えているつもりですが、記事ではできていないかもしれないので、念の為各行でインデントが必要の場合は「#[2]」(インデント2つ)のように表記しておきます。
以下コード↓↓
Letters=["C","G","H","I","L","O","S"]
#-------------------------------------
def Let(x):
return Letters[x] #[1]
#-------------------------------------
def STH(X):
CHECK=[0,0,0,0,0,0,0] #[1]
Digits=[] #[1]
for j in range(10): #[1]
x= (X // 7**j)%7 #[2]
Digits.append(x) #[2]
for j in range(10): #[1]
y=Digits[j] #[2]
CHECK[y] = CHECK[y]+1 #[2]
if CHECK==[1,1,3,1,1,2,1]: #[1]
STRING=list(map(Let,Digits)) #[2]
STRING.reverse() #[2]
string1="".join(STRING__) #[2]
return [Digits,STRING__,string1] #[2]
else: #[1]
return [-1] #[2]
#-------------------------------------
def Checking(X,i):
if i==1: # Hが2連続だけする。Oは連続しない #[1]
x=("HH" in X) #[2]
y=not("OO" in X) #[2]
z=not("HHH" in X) #[2]
return x * y * z #[2]
if i==2: # 同じ文字が連続しない #[1]
x=not("HH" in X) #[2]
y=not("OO" in X) #[2]
return x * y #[2]
if i==3: #[1]
x=("HO" in X[0:2])+("HO" in X[1:3])+("HO" in X[2:4])+("HO" in X[3:5])+("HO" in X[4:6])+("HO" in X[5:7])+("HO" in X[6:8])+("HO" in X[7:9])+("HO" in X[8:10])+("HO" in X[9:11]) #[2]
y=not( "HOH" in X) #[2]
z=not( "HOO" in X) #[2]
w=not("HHO" in X) #[2]
v=not("OHO" in X) #[2]
a=(x==1) #[2]
return y * z * w * v * a #[2]
#-------------------------------------
#print(STH(9876543210)) 例
count=0
for i in range(7689660,275589972+1):
M=STH(i) #[1]
if M!=[-1]: #[1]
STRING=M[2] #[2]
if Checking(STRING,3)==1: # i=1なら(2), i=2なら(3), i=3なら(4) が確認可能 #[2]
count+=1 #[3]
print("◯:",STRING, " , ",count) #[3]
else: #[2]
print("×:",STRING) #[3]
print(count,"個")
↑↑以上コード。あとはインデントの指示に従って入れればコードを実行できます。
$ $
問題4 (6/28作問)
$n \geq 2$ とし、集合$S_n=\left\{x\in\mathbb{Z} \;| \; 0\leq x< n\right\}$ とする。
$S_n$に対して、次の操作$A_n$を行う。
[操作$Aₙ$]
すべての$x\in S_n$に対して、$2x \equiv y \pmod n$ を満たす $S_n$ の要素$y$をすべて考え、それぞれに対して「$x \rightarrow y$」のようにして、$x$と$y$を矢印で繋げる。$2x \equiv x \pmod n$ ならば、$x \rightarrow x$ と繋げる。
矢印を繋いでできたまとまりを$1$つの「チェーン」と呼ぶことにする。
$ $
例:$n=6$のとき、チェーンは$2$個できる。
以下$ \pmod 6$
\begin{aligned} \qquad &0\times 2 =0 \equiv 0 , \qquad 1\times 2 =2 \equiv 2 , \qquad 2\times 2 =4 \equiv 4 ,\\ \qquad &3\times 2 =6 \equiv 0 , \qquad 4\times 2 =8 \equiv 2 , \qquad 5\times 2 =10 \equiv 4 \end{aligned}
$n=6$
例:$n=7$のとき、チェーンは3個できる。
以下$ \pmod 7$
\begin{aligned} \qquad &0\times 2 =0 \equiv 0 , \qquad 1\times 2 =2 \equiv 2 , \qquad 2\times 2 =4 \equiv 4 , \qquad 3\times 2 =6 \equiv 6 , \\ \qquad &4\times 2 =8 \equiv 1 , \qquad 5\times 2 =10 \equiv 3 , \qquad 6\times 2 =12 \equiv 5 \end{aligned}
$n=7$
このとき、次の問いに答えよ。
$\displaystyle (1)$ $n=15$のとき、チェーンは何個できるか。
$\displaystyle (2)$ $n$が奇数のとき、どのチェーンも$n=6$のように枝分かれすることなく、$n=7$のように環状にできることを示せ。
$\displaystyle (3)$ $n=2^k-1\;(k\geq2)$ のとき、$i=0,1,2,...,k-1$に対して $d_i \in \left\{0,1\right\}$ とする。
$\hspace{2.5em}$ $\displaystyle x=\sum_{i=0}^{k-1} 2^id_i \quad=2^{k-1}d_{k-1}+2^{k-2}d_{k-2}+\dots+2^2d_2+2^1d_1+d_0$
$\hspace{1.5em}$で表される$x\in S_n$について、$y\equiv 2x \pmod n$ かつ $y\in S_n$ を満たす整数$y$を、$d_0,d_1,d_2,\dots ,d_{k-1}$を用いて表せ。
$\displaystyle (4)$ $n=4095$のとき、チェーンは何個できるか。
$ $
以下解答です。
$\text{(1)}$解答(答えのみ)
$5$個
$ $
$\text{(1)}$解説
列挙していくだけである。
\begin{aligned} &0 &\rightarrow (0) \\ &1 \rightarrow 2 \rightarrow 4 \rightarrow 8 &\rightarrow (1) \\ &3 \rightarrow 6 \rightarrow 12 \rightarrow 9 &\rightarrow (3) \\ &5 \rightarrow 10 &\rightarrow (5) \\ &7 \rightarrow 14 \rightarrow 13 \rightarrow 11 &\rightarrow (7) \\ \end{aligned}
従って、チェーンは$5$個できる
$ $
$\text{(2)}$証明
題意を示すには、$n$が奇数のとき
$①$どの数$x$についても、その数を始点とするような矢印をただ一本引くことができる。
$②$どの整数$y$についても、その数を終点とするような矢印をただ一本引くことができる。
$③$どの数字もチェーンを辿れば同じ数字に戻ってくる。
の$3$つを示せばよい。
$①$どの整数$x$に対しても$2x$である整数はただ一つ存在し、$2x$を$n$で割った余り$y$もただ一つ存在する。従ってどの数$x$についても、その数を始点とするような矢印をただ一本引くことができる。
$②$これを示すには、$n$が奇数のとき「すべての整数$y\;(0 \leq y < n)$ に対して $2x\equiv y \pmod n$ を満たす整数$x$が$0 \leq x < n$の範囲にただ一つ存在する」ことを示せばよい。
$n$を奇数とする。
$0 \leq x < n$のとき$0 \leq 2x <2n$ であるから、$\displaystyle y\equiv 2x \pmod n \quad\Leftrightarrow 2x=y \text{ or } 2x=n+y \quad \Leftrightarrow x=\frac{y}{2} \text{ or } x=\frac{n+y}{2}$
$\text{(i)}$ $y$が偶数のとき
$\hspace{2em}$ $2x$が偶数より $\displaystyle x=\frac{n+y}{2}$ は不適。$\displaystyle x=\frac{y}{2}$ は適する。
$\text{(ii)}$ $y$が奇数のとき
$\hspace{2em}$ $2x$が偶数より $\displaystyle x=\frac{y}{2}$ は不適。$\displaystyle x=\frac{n+y}{2}$ は適する。
従って、$y\equiv 2x \pmod n$ を満たす$x\in S_n$ はただ一つ存在し、それは
\begin{aligned} x=\begin{cases} \displaystyle \frac{y}{2} &( y \text{ : 偶数}) \\ \displaystyle \frac{n+y}{2} &( y \text{ : 奇数}) \end{cases} \end{aligned}
である。
以上から、どの整数$y$についても、その数を終点とするような矢印をただ一本引くことができる。
$③$ 整数の数列$\left\{a_i\right\} \; (i=0,1,2,...)$の項が、すべて$a_i \in S_n$, $a_{i+1}\equiv 2a_i \pmod n$ を満たしているとすると、それらは$a_0 \rightarrow a_1 \rightarrow a_2 \rightarrow \dots \rightarrow a_n \rightarrow \dots$の関係にある。
ところで、この数列のはじめから$n+1$個の数$a_i\;(i=0,1,2,...,n)$は、$n$個の整数を要素に持つ集合の要素であるから、鳩の巣原理により少なくとも$1$組は同じ値である。
$T$を$n$以下の自然数として同じ値である$2$項を$a_j=a_{j+T} \; (0\leq j< j+T\leq n)$であるとすると、$①②$から$\left\{a_i\right\}(i=0,1,2,...)$は常に$a_i=a_{i+T}$を満たす。
したがって、$n$が奇数のときチェーン$a_0 \rightarrow a_1 \rightarrow a_2 \rightarrow \dots \rightarrow a_{T-1} \rightarrow (a_0)$はこの順に環状になる。
これはどのチェーンにも言えるため、$n$が奇数ならばチェーンはすべて環状である。
$ $
$\text{(3)}$解答(答えのみ)
$\displaystyle y= d_{k-1}+\sum_{i=1}^{k-1} 2^id_{i-1}$
$\displaystyle \hspace{0.3em}\left( =2^{k-1}d_{k-2}+2^{k-2}d_{k-3}+\dots+2^3d_2+2^2d_1+2^1d_0+d_{k-1} \right)$
$ $
$\text{(3)}$解説
$\displaystyle x=\sum_{i=0}^{k-1} 2^id_i$であるから、$\displaystyle 2x=\sum_{i=0}^{k-1} 2^{i+1}d_i \quad =2^kd_{k-1}+\sum_{i=1}^{k-1} 2^id_{i-1}$
また、$x<2^k-1$であるから、$d_0=d_1=d_2=\dots=d_{k-1}=1$となることはない。
以下$\mod (2^k-1)$ として、
\begin{aligned} y &\equiv 2x \\ &\equiv 2^kd_{k-1}+\sum_{i=1}^{k-1} 2^id_{i-1} \\ &\equiv d_{k-1}+\sum_{i=1}^{k-1} 2^id_{i-1}\\ \end{aligned}
ここで、$\displaystyle 0\leq d_{k-1}+\sum_{i=1}^{k-1} 2^id_{i-1}< 1+\sum_{i=1}^{k-1}2^i=2^k-1$であるから、
$y$が$0\leq y< 2^k-1$ を満たすことを踏まえて$\displaystyle y= d_{k-1}+\sum_{i=1}^{k-1} 2^id_{i-1}$
$\displaystyle \left( \therefore y=2^{k-1}d_{k-2}+2^{k-2}d_{k-3}+\dots+2^3d_2+2^2d_1+2^1d_0+d_{k-1} \right)$
$ $
$ $
$\text{(4)}$解答(答えのみ)
$351$個
$ $
$\text{(4)}$解説
$4095=2^{12}-1$である。
$x\in S_{4095}$とする。
どの$x$に対しても常に$2^{12}x\equiv x\pmod {4095}$ が成立するから、$(2)$を踏まえると、どのチェーンも$12$の正の約数の長さ(一周するまでの$\rightarrow$の個数)をもつ。
ここで、以下 $\mod 4095$ とする。
任意の$i=0,1,2,\dots,11$について$d_i\in\left\{0,1\right\}$を満たすような$d_0,d_1,d_2,\dots,d_{11} \;(d_0\cdot d_1\cdot d_2\cdot \dots \cdot d_{10}\cdot d_{11}=0)\;$を用いて、$x\in S_{4095}$である$x$を
$\displaystyle x=2^{11}d_{11}+2^{10}d_{10}+2^9d_9+2^8d_8+\dots+2^2d_2+2^1d_1+2^0d_0$
と表すとき、$x\rightarrow y$であるような$y\in S_{4095}$について
\begin{aligned} y&\equiv 2x \\ &\equiv 2^{12}d_{11}+2^{11}d_{10}+2^{10}d_9+2^9d_8+\dots+2^3d_2+2^2d_1+2^1d_0\\ &\equiv 2^{11}d_{10}+2^{10}d_9+2^9d_8+\dots+2^3d_2+2^2d_1+2^1d_0+d_{12}\\ \therefore &\quad y=2^{11}d_{10}+2^{10}d_9+2^9d_8+\dots+2^3d_2+2^2d_1+2^1d_0+d_{12} \end{aligned}
したがって、$x\;(\in S_{4095})$を$2$進法で表記したとき、$x\rightarrow y$を満たす$y \;(\in S_{4095})$は、その$2$進法表記が「$x$が$2$進法表記で表す文字列に対して、左端の数字をを右端に移動させたもの」であるといえる。
例:
$\displaystyle 3761\rightarrow 3427$
$\displaystyle 3761_{(10)}=111010110001_{(2)}$
$\displaystyle 3427_{(10)}=110101100011_{(2)}$
$x\rightarrow y$ である$x,y$は同じチェーンにあるため、
$n=4095$のときのチェーンの個数を数えるには、
「$0,1$の$2$種類の文字を$12$個並べる方法(ただし例のように循環すると長さ$12$の同じ文字列が現れるものを同じ並べ方とみなす)」を数えればよい。
これは言い換えれば
円周上に等間隔に$12$個の頂点を配置し、各頂点を白$(0)$と黒$(1)$で塗り分ける方法(ただし回転して同じ色の配置となるものは同じ塗り方とする)であるといえる。
ただし、$4095\not\in S_{4095}$であるから、すべて黒である塗り方は除外する必要がある。(後ほど除外する。)
以下、同じ色の配置となる循環節の長さがちょうど$1,2,3,4,6,12$個となるものを数えていく。
$\text{(i)}$ 循環節の長さが$1$のとき、チェーンの長さは$1$
$\hspace{1em}$ 白$(0)$が$12$個並ぶか黒$(1)$が$12$個並ぶかの$2$通り
$\text{(ii)}$ 循環節の長さが$2$のとき、チェーンの長さは$2$
$\hspace{1em}$ $($循環節の色の並べ方の総数$2^2)$$-(\text{(i)}$の並べ方の総数$2)$ $=2$通り
$\text{(iii)}$ 循環節の長さが$3$のとき、チェーンの長さは$3$
$\hspace{1em}$ $($循環節の色の並べ方の総数$2^3)$$-(\text{(i)}$の並べ方の総数$2)$ $=6$通り
$\text{(iv)}$ 循環節の長さが$4$のとき、チェーンの長さは$4$
$\hspace{1em}$ $($循環節の色の並べ方の総数$2^4)$$-(\text{(i)}$の並べ方の総数$2)$ $-(\text{(ii)}$の並べ方の総数$2)$ $=12$通り
$\text{(v)}$ 循環節の長さが$6$のときチェーンの長さは$6$
$\hspace{1em}$ $($循環節の色の並べ方の総数$2^6)$$-(\text{(i)}$の並べ方の総数$2)$ $-(\text{(ii)}$の並べ方の総数$2)$ $-(\text{(iii)}$の並べ方の総数$6)$ $=54$通り
$\text{(vi)}$ 循環節の長さが$12$のときチェーンの長さは$12$
$\hspace{1em}$ $($循環節の色の並べ方の総数$2^{12})$$-(\text{(i)}$の並べ方の総数$2)$ $-(\text{(ii)}$の並べ方の総数$2)$ $-(\text{(iii)}$の並べ方の総数$6)$ $-(\text{(iv)}$の並べ方の総数$12)$ $-(\text{(v)}$の並べ方の総数$54)$ $=4020$通り
したがって、チェーンの個数は、$\text{(1)}$ですべて黒が並ぶ場合を除外して
$\displaystyle (2-1)+\frac{2}{2}+\frac{6}{3}+\frac{12}{4}+\frac{54}{6}+\frac{4020}{12}=351$個である。
$ $
あとがき
最後に作ったのが$\text{(3)}$なんですが、最初に$3$問作ったときに友達から「どうせならもう$1$問作って$4$問にしないか」と言われたので作りました。
また、7月に いいねの数だけ作問をするツイート をしたので、今回は$\text{(2)(3)}$を最初の$2$問とさせてください。
更新欄
2025.7.13.8:50 投稿
~ 2025.7.13.16:15 少々修正
2025.7.14 誤字など修正
