文献あり

OMC攻略①　動的計画法

230

動的計画法(Dynamic Programming)とはアルゴリズムの一種であり、
対象となる問題を複数の部分問題に分割し、部分問題の計算結果の記録を利用して全体の問題を解く手法を総称してこう呼ぶ。
これは競技プログラミングでの用途が一般的であるが、数学にも役立つことがある。そのため、私は数学の訓練のために競技プログラミングをやることを推奨している。

数学における動的計画法は、
①途中までの計算結果を記録するという発想
②手計算で地道に漸化式を解く
この2つの条件を満たすことが多い。
今回の記事では、N^2以上の盤面を使うことにフォーカスする。

簡単な例(小学生式)

下の図において、ゆーてる君は各マスで右か上に1マスずつ進める。スタートからゴールまで最短距離で移動する経路はいくつあるか
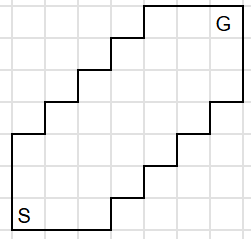迷路ー！

「右または上」が重要。つまり、今ゆーてるがいるマスは、必ず左または下から来たことになる。これを利用して漸化式を立てよう。
「漸化式」っていう難しい言葉が出てくるけど、やることは簡単。
各マスに移動する場合の数を考えて、左下から順に、各マスに「左の数と下の数の合計」を書き込めば良い。
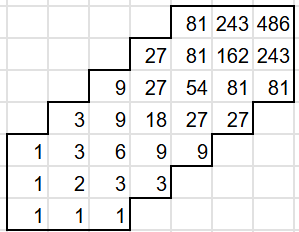見ろ！これが噂の動的計画法だ！
よって答えは486

※この最短経路の問題は興味深い。
この場合、3の累乗っぽい規則性が見られるだろう。
それもそのはず、規則的な形のときはこの2次元の漸化式は規則性をもつことがわかっている。
長方形ならパスカルの三角形になるし、
階段型ならカタラン数になる。

実はこれから見せる3問は、これと本質的に同じである。

OMCB040(G)

　OMC君は正 6 面体，正 8 面体，正 12 面体，正 20 面体のサイコロをそれぞれ 11 つずつ持っています．また，各 k∈{6,8,12,20}に対し正 k 面体のサイコロを振ったときに出る目は 1 以上 k 以下の整数であり，それぞれの目は等確率で現れるものとします．　OMC君はこれら 4 つのサイコロを同時に振ります．このときに現れる正 6面体，正 8 面体，正 12面体，正 20 面体のサイコロの目をそれぞれ a,b,c,d としたとき，a<b<c<dとなる確率は互いに素な正整数 m,n
によって m/n と表せるので，m+nの値を解答して下さい．

変に工夫して計算ミスをするより、動的計画法を用いた方が速く、正確になる最たる例だと思います。

解き方　by MARTH

1≤a≤6,1≤b≤8,1≤c≤12,1≤d≤20であって,a<b<c<dを満たす正整数の組の数を N とすれば, 答えの確率は N/6⋅8⋅12⋅20 である.
　N を求めることを考える. 座標平面内で(0,0)→(0,a−1)→(1,a−1)→(1,b−2)→(2,b−2)→(2,c−3)→(3,c−3)→(3,d−4)と x,yいずれか正方向に 1 ずつ進むことを繰り返して移動する経路と (a,b,c,d) の組を一対一に対応させることができる. あとは表のようにして, 各セルについて真下のセルと左のセルの和を書き込む。 1番右の列のセルの値を全部足し合わせると、N=1768になり、
答えは1768/11520=221/1440

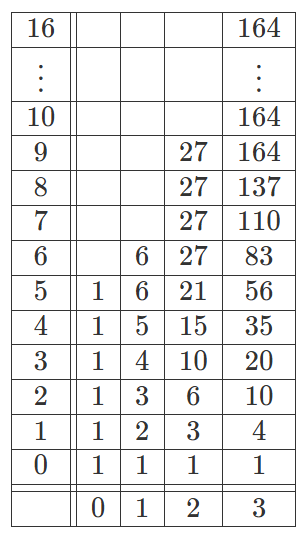表

よって解答するべき値は221+1440=1661

日本数学オリンピック予選2022第9問

1,2,⋯,1000 の並び替え(p1,p2,⋯,p1000)であって、任意の1以上999以下の整数iに対して、piがiの倍数であるようなものはいくつあるか。

この問題は動的計画法(?)が想定解であるため、裏技として紹介する感じではありません。発想としては重要です。
解法はてきとうにネットで調べたら見つかります。

OMCE016(B)

$\displaystyle \begin{array}{{>{\displaystyle}l}} 　30個の整数の組 (x_1,…,x_{10},y_1,…,y{10},z_1,…,z_{10})であって，\\ 以下の条件をともにみたすものは全部でいくつありますか？\\ ・任意の 1≤n≤9 なる整数 n について，x_{n+1}−x_n，y_{n+1}−y_n，\\z_{n+1}−z_nのうち 1つは 1 に等しく，残り 2 つは 0 に等しい．\\ ・任意の 1≤n≤10 なる整数 n について，\\max⁡(∣x_n∣,∣y_n∣,∣z_n∣)=2，min⁡(∣x_n∣,∣y_n∣,∣z_n∣)<2をともにみたす． \end{array}$

これは私が考えた解法です。裏技テクニックとして感心してくれると嬉しいです。模範解答では幾何学的な議論が必要だが、このやり方はゴリ押ししか使っていない。
条件から、
$ x_{10}+y_{10}+z_{10}=x_1+y_1+z_1+9$
よって$(x_1,y_1,z_1)\rightarrow(x_{10},y_{10},z_{10})$について、x,y,zで入れ替えたものを省いたとき、
①(-2,-2,-1)→(2,2,0)
②(-1,-2,-2)→(2,2,0)
③(-2,-2,-1)→(1,1,2)
④(-2,-2,-1)→(2,1,1)
の4つに場合分けできる。
※(-2,-1,-1)→(2,2,1)などは正負を反転しただけだから含めない。最後に2倍することで帳尻合わせをする。

あとは、①~④を動的計画法で解いたらいい。
これ以降x軸は右方向、y軸は上方向、盤面はzが小さい順から左から並べるものとする。盤面のXは、問題文の2つ目の条件から通過することができないことを意味する。
①x,y,zの並び順で×3をする。
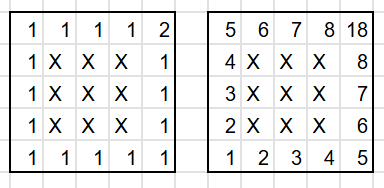①(左がz=-1,右がz=0)
よって18×3=54
②x,y,zの並び順で×6をする。
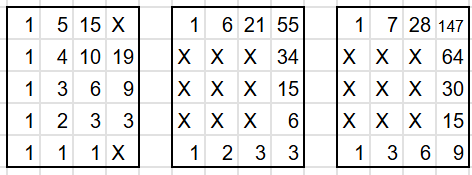②
よって147×6=882
③x,y,zの並び順で×3をする。
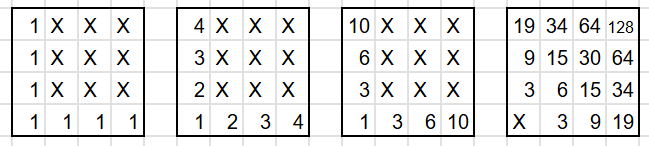③
よって128×3=384
④x,y,zの並び順で×6をする。
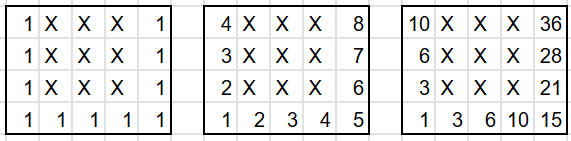④
よって36×6=216