トーナメントが環境の偏りを拡大する？！ ー勝ち上がりに伴う環境の変化を計算するー

はじめに

カードゲームなどのトーナメント大会で大会上位が変わったデッキであふれるという経験はないでしょうか？

最近 興味深いツイート がバズりました。
発端ツイートのスクショ

参加者全体で見るとうんちビートの使用率が高いとしても、トーナメントを勝ち進んだ上位卓では、うんちビートに有利なちんちんコントロールデッキばかりになっているかもしれません。そうなると、コントロールデッキに有利な別のデッキが、さらなる勝ち上がりには有効になるはずです。

このように、トーナメントの進行度によって、有効なキャラクターや戦略は変化していく可能性があります。本記事では、この「トーナメントの勝ち上がりに伴うキャラクター使用率の変化」という現象を、数理的なモデルを使って解き明かしていきます。

目的

この記事でわかること

• トーナメントを勝ち進むにつれて、なぜメタゲームの偏りが拡大していくのか、そのメカニズム
• メタゲームの予測がなぜ難しいのか、その構造的な理由
• トーナメント環境におけるキャラクター使用率の変化を分析する数学的なモデル

この記事でわからないこと

• 特定の状況でどのキャラクターを使えば勝てるかといった具体的な戦略（本稿が示すのは、予測が「困難である」という構造です）

本記事の目的は、ゲーム理論の考え方を用いて、「トーナメント」というシステムが、いかにして初期のわずかな環境の偏りを拡大させ、メタゲームの予測を困難にしていくのか、そのプロセスを数学的なモデルを通して解き明かすことです。

そのために、本稿では数理モデルを用いて、以下のステップで分析を進めます。

1. キャラクター間の相性（勝率）を行列で表現する
   どのキャラクターがどのキャラクターに有利・不利であるかを「利得行列」として定義します。
2. トーナメントの勝ち上がりを数式でモデル化する
   あるラウンドでのキャラクター使用率が、次のラウンドでどのように変化するのかを、漸化式を用いて表現します。
3. 「環境の偏り」がトーナメントに与える影響を分析する
   理想的な「ナッシュ均衡」の状態から少しだけズレた「偏った」環境が、トーナメントを勝ち進むにつれてどのように変化していくのかを分析します。

これらの分析を通じて、「なぜトーナメント上位のメタゲームは、これほどまでに予測が困難なのか？」という問いに対し、その根底にある構造的な理由を提示します。

理論：トーナメントを数式でモデル化する

それでは、実際にトーナメントの勝ち上がりを数式でモデル化していきましょう。少し複雑に見えるかもしれませんが、一つ一つのステップを丁寧に解説していきます。

問題設定

まず、トーナメントの状況を以下のように設定します。

• m種類 のキャラクターが存在する。
• $2^n$人 のプレイヤーがトーナメントに参加する。
• 各プレイヤーは、m種類のキャラクターのうちいずれか1つを使用する。
• キャラクター間の勝率は、どのプレイヤーが使用しても常に一定である。

$2^n$人のトーナメントなので、優勝するためにはn回勝利する必要があります。例えば、参加者が256人なら $2^8$ なので、8回戦を勝ち抜けば優勝となります。

利得行列 A：キャラクター間の相性を表現する

キャラクター間の相性（勝率）を、利得行列 A というm×mの行列で表現します。行列のi行j列の要素 $A_{ij}$ は、「キャラクターiがキャラクターjと対戦した時の勝率」を表します。一般に利得行列の話をする場合は利得として勝率以外を取ることもありますが、今回のトーナメントの勝ち上がりでは勝率(勝ち上がれる確率)を行列要素として話を進めます。

例えば、3すくみ（グー・チョキ・パー）のような関係であれば、行列は以下のようになります。（あいこは50%で勝ち上がるものとします）
$$ A = \begin{pmatrix} 0.5 & 1 & 0 \\ 0 & 0.5 & 1 \\ 1 & 0 & 0.5 \end{pmatrix} $$
(行と列はそれぞれグー、チョキ、パーに対応)

あるラウンドで、キャラクターiを使用しているプレイヤーが対戦相手と当たるわけですが、その対戦相手がどのキャラクターを使っているかは、そのラウンドのキャラクター使用率によって決まります。キャラクターの使用率をm次元のベクトル u で表すと、キャラクターiを使っているプレイヤーが次のラウンドに勝ち上がれる確率（期待値）は、行列とベクトルの積 Au の第i成分として計算できます。

漸化式：勝ち上がりによる使用率の変化

あるラウンド（n'回戦）が終了した時点でのキャラクター使用率の期待値をベクトル $u^{(n')}$ で表すことにします。

n'回戦に参加しているキャラクターiの割合は $u^{(n')}_i$ です。そして、そのキャラクターiがn'回戦で勝利する確率は $(Au^{(n')})_i$ です。したがって、n'+1回戦に進出するキャラクターiの割合は、この二つの積に比例します。

これを数式で表すと、次のラウンド $u^{(n+1)}$ の使用率は、現在のラウンドの使用率 $u^{(n)}$ を使って以下のような漸化式で計算できます。
$$ u^{(n+1)}_i = C \cdot u^{(n)}_i \cdot (Au^{(n)})_i $$
ここで、Cは規格化定数で、全キャラクターの使用率の合計が1になるように調整するためのものです。1試合ごとに参加者が半分になるので、C=2となります。

この式を繰り返し適用していくことで、トーナメントの初期状態 $u^{(0)}$ から、任意のラウンド $n'$ における使用率 $u^{(n')}$ を計算することができます。

ナッシュ均衡の場合：使用率は変化しない

もし、初期のキャラクター使用率 $u^{(0)}$ が、ゲーム理論における「ナッシュ均衡」の状態 v であった場合、つまり $u^{(0)} = v$ の時、どうなるでしょうか。

ナッシュ均衡の定義より、どのキャラクターを選択してもナッシュ均衡の相手に対しては勝ち上がれる確率は等しくなります。つまり、ベクトル Av の全ての成分が $\frac{1}{2}$ になります。

この時、1回戦後の使用率 $u^{(1)}$ は漸化式より、
$$ u^{(1)}_i = 2 \cdot u^{(0)}_i \cdot (Au^{(0)})_i = 2 \cdot v_i \cdot (Av)_i = 2 \cdot v_i \cdot \frac{1}{2} = v_i $$
となり、$u^{(1)}=v$ となります。これを数学的帰納法により繰り返すと、どのラウンドでも使用率は v のまま変化しないことがわかります。

$$ u^{(n+1)}_i = u^{(n)}_i $$

となり、なんと トーナメントを勝ち上がっても使用率は全く変化しない という結果になります。つまり、環境が完全に均衡している場合、トーナメントの上位も下位もキャラクターの分布は同じになるのです。

偏った環境の場合：メタは回るのか？

しかし、現実のゲーム環境が完全にナッシュ均衡になっていることは稀です。多くの場合、少しだけ均衡からズレた「偏った」環境になっています。

この「偏り」を、均衡状態からの差分ベクトル δu として表現しましょう。つまり、初期のキャラクター使用率を $u^{(0)} = v + \delta u$ とします。（vはナッシュ均衡の使用率ベクトル）

この初期状態から、トーナメントが1回進むと、使用率の偏りはどう変化するでしょうか。導出の詳細は以下の通りです。

$$ \begin{align} u^{(n+1)}_i &= 2 u^{(n)}_i (A u^{(n)})_i \\ (v + \delta u^{(n+1)})_i &= 2 (v + \delta u^{(n)})_i (A (v + \delta u^{(n)}))_i \\ v_i + \delta u^{(n+1)}_i &= 2 (v_i + \delta u^{(n)}_i) \sum_j A_{ij} (v_j + \delta u^{(n)}_j) \\ &= 2 (v_i + \delta u^{(n)}_i) (\sum_j A_{ij} v_j + \sum_j A_{ij} \delta u^{(n)}_j) \\ &= 2 (v_i + \delta u^{(n)}_i) ((Av)_i + (A \delta u^{(n)})_i) \end{align} $$

ここで、vはナッシュ均衡なので、 $(Av)_i = 1/2$ です。
$$ \begin{align} v_i + \delta u^{(n+1)}_i &= 2 (v_i + \delta u^{(n)}_i) (1/2 + (A \delta u^{(n)})_i) \\ &= (v_i + \delta u^{(n)}_i) (1 + 2(A \delta u^{(n)})_i) \\ &= v_i + 2 v_i (A \delta u^{(n)})_i + \delta u^{(n)}_i + 2 \delta u^{(n)}_i (A \delta u^{(n)})_i \end{align} $$

$\delta u$ は微小量なので、2次の項 $\delta u^{(n)}_i (A \delta u^{(n)})_i$ は無視できるとすると

$$ \begin{align} v_i + \delta u^{(n+1)}_i &\approx v_i + 2 v_i (A \delta u^{(n)})_i + \delta u^{(n)}_i \\ \delta u^{(n+1)}_i &\approx \delta u^{(n)}_i + 2 v_i (A \delta u^{(n)})_i \\ &= \delta u^{(n)}_i + 2 v_i \sum_j A_{ij} \delta u^{(n)}_j \end{align} $$

この式を行列で表現すると、次のラウンドの歪み δu' は、以下のような線形変換で表せることがわかります。

$$ \delta u^{(n+1)} = B \cdot \delta u^{(n)} $$

ここで、B は m×m の行列で、$B_{ij} = \delta_{ij} + 2v_i A_{ij}$ という式で定義されます。（$\delta_{ij}$はクロネッカーのデルタ）

この結果は非常に重要です。つまり、トーナメントを1ラウンド勝ち進むごとに、均衡からの歪み（メタのズレ）は行列Bによって変換されていく ことを意味します。

これをn回繰り返すと、n回戦終了後の歪みは以下のようになります。
$$ \delta u^{(n)} = B^n \cdot \delta u^{(0)} $$
最終的に、n回戦終了後のキャラクター使用率は、
$$ u^{(n)} = v + B^n \cdot \delta u^{(0)} $$
と表すことができます。この式が、私たちの分析の核心となります。

考察：メタはなぜ、どのように回るのか？

理論の章で、トーナメントを勝ち進むごとに、環境の「偏り」 δu が行列 B によって変換されていく、という数式を導き出しました。
$$ u^{(n)} = v + B^n \cdot \delta u^{(0)} $$

この一見すると複雑な式が、トーナメントにおけるメタゲームのダイナミクスを解き明かす鍵となります。この式を紐解くことで、「メタが回る」という現象の基本的な性質から、その詳細なふるまいまでを数学的に理解することができるのです。

数式が示すメタゲームの基本的な性質

まず、この数式から直接的にわかる、メタゲームの最も重要な3つの性質について見ていきましょう。

メタゲームの原動力は「均衡からの偏り」

この分析から得られる最も重要な知見は、メタゲームの動向を決定するのは、キャラクターの絶対的な使用率の高さではなく、ナッシュ均衡という理想的な状態からどれだけ偏っているか（過大評価／過小評価されているか） という点です。

数式 $u^{(n)} = v + B^n \cdot \delta u^{(0)}$ を見てください。n回戦後の使用率 $u^{(n)}$ がナッシュ均衡 $v$ から変化する理由は、右辺の $B^n \cdot \delta u^{(0)}$ の項があるからです。そして、この $\delta u^{(0)}$ こそが、大会初期における「ナッシュ均衡からの偏り」を表しています。もし初期環境が完全にナッシュ均衡であれば ($\delta u^{(0)} = 0$)、この項は消え、何回戦勝ち進んでも使用率は $v$ のまま変化しません。

たとえあるキャラクターの使用率が全体の50%を占めていたとしても、それがナッシュ均衡通りの比率なのであれば、そのキャラクターがトーナメントで有利になることも不利になることもないのです。

一方で、使用率がわずか5%しかないキャラクターでも、ナッシュ均衡における適正な比率が1%だったとすれば、それは「4%分も過大評価されている」ことになります。この「過大評価」こそが、メタを動かす原動力となるのです。

ラウンド数とメタの変化

次に数式の $B^n$ の部分、特に n（回戦） に注目してみましょう。このnが大きくなるほど、$B^n$ の影響は大きくなります。これは、トーナメントの規模や回戦数によって、メタゲームの様相が大きく変わることを意味します。
例えば、ごく小規模な大会（nが小さい）では、$B^n$ の効果が十分に現れる前に大会が終わってしまいます。そのため、初期環境の偏りはあまり増幅されず、メタは比較的穏やかなままです。

しかし、何回も勝ち進む必要がある大規模な大会（nが大きい）では、$B^n$ の効果が顕著に現れます。初期のわずかな偏りが、回戦を重ねるごとに繰り返し変換されていきます。そして、後のセクションで詳しく見ますが、この変換は多くの場合、偏りをさらに拡大する方向に作用します。その結果、上位環境では初期環境とは全く異なる、極端に偏ったメタゲームが形成されるのです。

したがって、「初戦を突破するのに有利なキャラクター」と「トーナメントを勝ち上がって上位に進出するのに有利なキャラクター」は、必ずしも同じではない、という可能性が生まれます。

有利なキャラクターの変遷

最後に、偏りを変換する行列 B そのものに注目します。行列 B は、単にズレ$\delta u^{(0)}$ を拡大・縮小するだけではありません。ベクトルの「向き」を変える働きも持っています。

これは、ラウンドが進むごとに、有利になる（過大評価される）キャラクターが順番に移り変わっていく という現象を引き起こす可能性があります。

例えば、初期環境ではキャラクターAが過大評価されていたとします（$\delta u^{(0)}$ のAに対応する成分が大きい）。しかし、行列Bを掛けることで、その偏りの形が変わり、数回戦後にはキャラクターBが最も過大評価される、という状況に変化することがあるのです。

このように、メタゲームは静的なものではなく、トーナメントの進行とともに有利なキャラクターが移り変わっていく動的なプロセスであることが、このモデルから示唆されます。

詳細なふるまい：行列Bの固有値が鍵

さて、これまでメタゲームの基本的な性質を説明してきましたが、では「偏り」は具体的にどのように、どのくらいの速さで変化していくのでしょうか？その鍵を握るのが、行列 B の数学的な性質、特に「固有値」という概念です。

行列 B をn乗するということは、ざっくり固有値もn乗されていくことを意味します。Bの固有値が1を超えていればn乗した時にどんどん大きくなり、1未満であればn上により小さくなるという事です。 B の固有値を調べることで、トーナメントが進むにつれて環境の歪みがどうなっていくのか、その未来をより詳細に予測できるのです。

このモデルをいくつかの具体的なケースで計算してみると、非常に興味深く、そして意外な結論が浮かび上がってきます。それは、多くの場合で 行列B の固有値の絶対値が1より大きくなる という事実です。

当初、わたしは「トーナメントが進むほど、メタは安定したナッシュ均衡に収束していくのではないか（＝固有値の絶対値が1未満になるのではないか）」と予想していました。しかし、複数の例で試す限り、結果は真逆でした。固有値の絶対値が1より大きいということは、ナッシュ均衡からのわずかなズレが、トーナメントを勝ち進むごとに拡大していく ことを意味します。

これは、ナッシュ均衡という一点が、実は非常に不安定なバランスの上に成り立っていることを示唆しています。ほんの少しでも均衡からズレた状態からスタートすると、そのズレはラウンドが進むにつれて雪だるま式に大きくなり、全く予測のつかない魔境へと突き進んでいくのです。

具体例：グラフで見るメタゲームの動き

理論と考察の章では、トーナメントにおけるメタゲームの動向が「ナッシュ均衡からのズレ」によって引き起こされることを数式を用いて説明しました。しかし、数式だけではなかなかイメージが湧かないかもしれません。

この章では、具体的な2つの例「うんちビート」と「じゃんけん」を取り上げ、グラフを使いながら、実際にメタゲームがどのように動いていくのかを視覚的に見ていきましょう。

例1：うんちビート ～使用率1位が勝者とは限らない～

まず、架空の3つのデッキタイプ「うんちビート」「ちんちんコントロール」「おっぱいミッドレンジ」が存在するメタゲームを考えてみます。それぞれの相性は以下の通りです。

• うんちビート：ちんちんコントロールに有利、おっぱいミッドレンジに不利
• ちんちんコントロール：おっぱいミッドレンジに有利、うんちビートに不利
• おっぱいミッドレンジ：うんちビートに有利、ちんちんコントロールに不利
  このメタゲームのナッシュ均衡（誰もデッキを変える動機がない安定状態）での各デッキの使用率は、うんち:ちんちん:おっぱい = 50% : 33.3% : 16.7% だとします。

では、大会開始時のプレイヤー全体の使用率が、ナッシュ均衡から少しズレて、うんち:ちんちん:おっぱい = 40% : 30% : 30% だったとしましょう。この状況を図で見てみます。

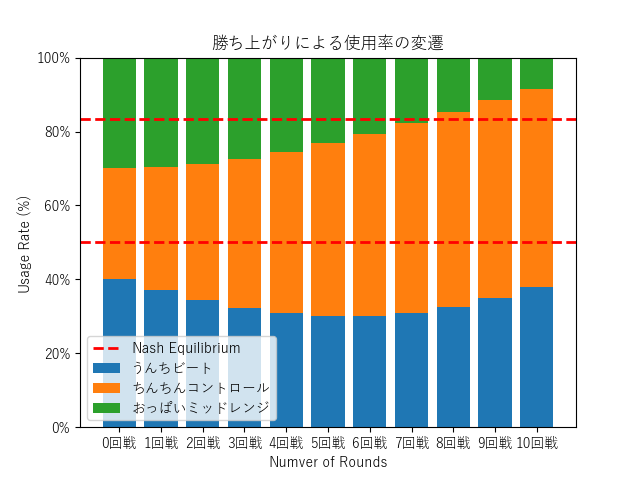初期環境とナッシュ均衡

グラフを見ると、開始時の環境（一番左、０回戦）では「うんちビート」（青）が最も使用率が高いことがわかります。しかし、トーナメントを勝ち進んでいくと、ちんちんコントロールの比率が多くなることがわかります。

なぜこのような逆転が起こるのでしょうか？
考察の章で述べた通り、メタを動かすのは「ナッシュ均衡からのズレ」です。今回の初期環境をナッシュ均衡と比べてみましょう。

• うんちビート: 均衡より10%少ない（過小評価）
• ちんちんコントロール: 均衡より3.3%少ない（過小評価）
• おっぱいミッドレンジ: 均衡より13.3%も多い（過大評価）
• この環境で最も「過大評価」されているのは、おっぱいミッドレンジです。そのため、おっぱいミッドレンジに有利なちんちんコントロールが最も勝ち上がりやすい環境と言えます。逆におっぱいミッドレンジに不利なうんちビートは、たとえ初期使用率が1位であっても、勝ち上がるにつれて数を減らしていきます。

また、ナッシュ均衡ぴったりの使用率だと次のように勝ち上がって分布が変わらないことが確認できます。
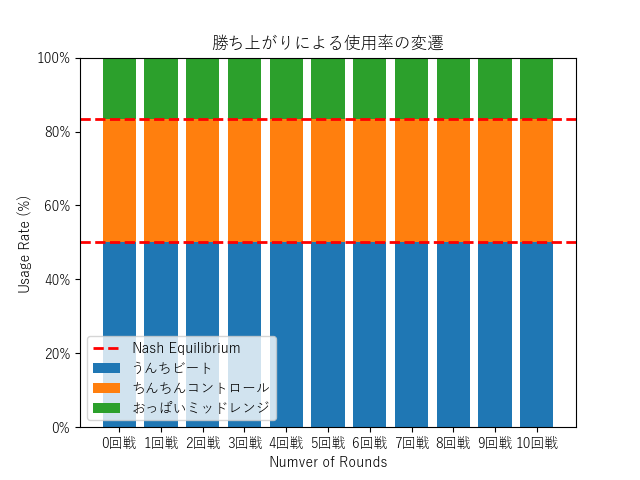初期環境とナッシュ均衡

これらの例からわかるように、あるデッキがトーナメントで有利かどうかは、単純な使用率の多さではなく、ナッシュ均衡と比べて「過小評価」されているかどうかで決まるのです。

例2：じゃんけん ～小さな差が大きな偏りを生む～

次に、私たちに最も馴染み深い「じゃんけん」を例に考えてみましょう。
ご存知の通り、じゃんけんのナッシュ均衡は、✊、✌️、✋をそれぞれ1/3ずつの確率で出すことです。もし✊、✌、✋を出すプレイヤーが完全に同じ比率で存在していたら✊✌✋は平等に勝ち上がります。

では、もし初期環境がナッシュ均衡からほんのわずかに、例えば✊:✌️:✋ = 38% : 33% : 28% のようにズレていたらどうなるでしょうか？

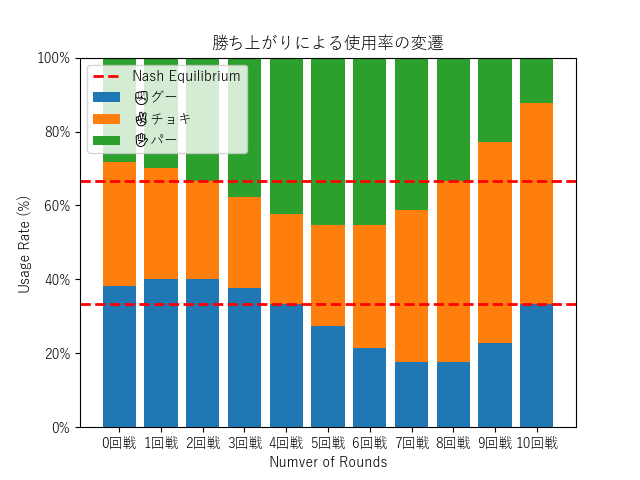じゃんけんのメタゲーム

グラフを見てください。初期環境(0回戦)では、✊、✌️、✋の差はごくわずかで、どれが一番多いかほとんど見分けがつきません。

しかし、トーナメントが進むにつれて、その差はどんどん拡大していきます。どの手の人数が一番多いかは何回戦かによって違いますが、右にいくほどトップの手と下位の手の使用率の差が激しくなってることがわかります。一番右の方なんて明らかに✋が少なくて✌多いです。

これは、考察の章で触れた「ナッシュ均衡からのわずかなズレが、トーナメントを勝ち進むごとに拡大していく」という性質を非常によく表しています。

じゃんけんのような一見すると完全に運に見えるゲームでさえ、参加者の傾向にほんのわずかな偏りがあるだけで、トーナメントの勝ち上がりというフィルターを通すことで、上位環境では無視できない大きな偏りが生まれるのです。

この2つの例を通して、数式が示していたメタゲームのダイナミクスを、少しでも直感的に感じ取っていただけたのではないでしょうか。

まとめ

本稿で提示した数式モデルは、トーナメントにおけるメタゲームのダイナミクスを解き明かすための強力なツールです。しかし、その分析から見えてくるのは、メタゲームの未来を正確に予言する単純な方法ではなく、むしろその複雑さと予測困難さです。

これまでの考察で明らかになった、メタゲームの重要な性質を3つのポイントにまとめます。

1. 評価すべきは「均衡からの差」である
   メタゲームの動向を左右するのは、キャラクターの単純な使用率ではなく、ナッシュ均衡という理想的な状態からどれだけズレているか、という「差」です。プレイヤーは「うんちビートが流行っている」という事実だけでなく、「うんちビートは本来の強さと比べて過大評価されていないか？」という、より深いレベルでの分析が求められます。

2. 上位と下位ではメタが異なる
   トーナメントは、回戦を勝ち進むごとに環境が変化していきます。そのため、序盤有利なデッキと、決勝を目指すためのデッキは全く異なる可能性があります。「今流行っているデッキ」や「上位で支配的になったデッキ」は自分の目標となる勝ち上がり数では裏目になるかもしれません。

3. 初期のわずかな誤差が拡大する
   大会初期のナッシュ均衡からのごくわずかなズレは、回戦を経るごとに雪だるま式に増幅されていきます。これは、大会開始時点の環境をどれだけ正確に把握したとしても、その中に含まれる小さな不確定要素が、上位環境の様相を全く予測不可能なものに変えてしまう可能性があることを意味します。

これら3つの性質は、いずれも大会上位のメタゲームを正確に予測することが極めて困難であるという一つの結論を示唆しています。

あとがき

感想

お疲れさまでした。今回はトーナメントを勝ち上がるにつれて使用率がどう変わるかというメタゲームを見てみました。

「使用率の絶対値ではなくて均衡からのズレだよ」は言われてみればそうかも、「勝ち上がるにつれて元々使用率低かったデッキが支配的になるよ」はそりゃそうだろという感じですが、「勝ち上がるにつれてズレが大きくなるよ」はかなりヤバい結果だったと思います。

この手の誤差って試合を繰り返すにつれて小さくなって一定値に収束するパターンはよく見かけるんですが、誤差がどんどん増えるパターンが身近にあるのは面白いです。大会で勝ち上がると極端な環境で戦うことになるのは笑えないですが・・・。

https://github.com/pyran19/tournament_usage_dynamics

記事ではグラフ作るくらいしか活躍しませんでしたが、数値計算で使用率の分布を計算するプログラムも作って色々遊べるようにしたので興味があったら誰か代わりに計算続けてみてください。

今後の応用について

例えば、ぱっと浮かぶ中ではこんな部分が気になりました。

•   どんなゲームでも同じことが言える？: 今回は特定のゲームの利得行列を使いましたが、一般の利得行列に対して固有値の傾向はどうなるでしょう。特に、固有値の絶対値が1より大きいという性質は、どんなゲームにも共通するのでしょうか。わたしがランダムに数値計算した限りは固有値が全部１より大きくなる傾向だったので一般的に証明できると思います。
•   メタの周期は変わらない？: 理論上は、メタが一周する周期は使用率に依存しないという結果が出ています($B^n \delta u$なので周期はBで決まる→u部分は関係ない)。実際に変わらないのかどうかやどういう時に周期が長くなる(=メタが変わりにくくなるか)を調べるとトーナメント形式により荒れやすい環境がどういう環境かわかりそうです。
•   シミュレーションで確かめてみよう: 今回は確率分布の漸化式という形でシミュレーションと理論予測を立てましたが、実際に何万回とトーナメント対戦を繰り返すシミュレーションを組んでみたら、今回と同じ結果になるのかどうか。確かめてみるのも面白そうです。
•   「流行り」と「強さ」は違う？: 「使用率が高い」ことと、個々のプレイヤーが勝ち進む確率は、似ているようで少し違います。勝ち抜く回数の期待値などを計算してみると、「流行っているけど、実は勝ちにくい」といったキャラクターが見つかるかもしれません。

また、トーナメントという非常に身近で一般的な対戦形式についての話なので専門家がちゃんと調べた内容がありそうな気もします。他の人の研究で関連したものを知ってる方いれば教えてもらえると喜びます。