積分定数とは何か
本記事は、積分定数とは何かについて概ね私見で述べたものです。また、基本的に高校数学の範囲で理解できるように書いたつもりなので、厳密性が疎かになっている部分があるかもしれません。
前提
積分定数とは不定積分の答えについてくることでお馴染みのアレです。というか不定積分以外で「積分定数」なるものが登場することはないと思いますが。まずは高校数学における不定積分の定義を確認しましょう。
微分して$f(x)$になる函数を$f(x)$の原始函数という。また、$f(x)$の原始函数全体を$f(x)$の不定積分といい、$\displaystyle\int f(x)dx$と表記する。
例えば定数$C$を用いて$x^2-x+C$と表される函数はどれも微分すると$2x-1$になり、逆に微分して$2x-1$になる函数は全てこの形で表されます。このことを一般的には
$$\int(2x-1)dx=x^2-x+C$$
と書きますね。
「全体」とは？
$\displaystyle\int f(x)dx$は何者なのでしょうか。通常は函数として扱われていると思いますが、定義文では原始函数「全体」と書かれています。高校数学で「全体」という言葉が使われるものといえば集合です。不定積分を原始函数全体の集合だと考えると色々と上手くいきます。つまり、
$$\int(2x-1)dx=\{x^2-x+c\mid c\in\mathbb R\}$$
ということです($\mathbb R$は実数全体の集合)。ここで、次の定義を導入します。
函数$f(x)$および函数からなる集合$X$に対し、
\begin{align*}
f(x)+X&=\{f(x)+g(x)\mid g(x)\in X\}\\
f(x)-X&=\{f(x)-g(x)\mid g(x)\in X\}\\
f(x)X&=\{f(x)g(x)\mid g(x)\in X\}\\
\end{align*}
と定める。また、函数からなる集合$X,Y$に対し、
\begin{align*}
X+Y&=\{f(x)+g(x)\mid f(x)\in X,\,g(x)\in Y\}\\
X-Y&=\{f(x)-g(x)\mid f(x)\in X,\,g(x)\in Y\}\\
\end{align*}
と定める。
このような表記は高校数学では馴染みがありませんが、大学数学ではそれなりに使われます。要は、この記事でだけのローカルルールではないという弁明です。この表記を使うと
$$\int(2x-1)dx=\{x^2-x+c\mid c\in\mathbb R\}=x^2-x+\mathbb R$$
ですから、積分定数$C$は実数全体の集合であるとの解釈ができます。この考え方の妥当性を、2つの具体例を通して見ていきます。
具体例
積分でよく躓きがちなところとして、2通りの計算
\begin{align*}
\int(x+1)^2dx&=\frac13(x+1)^3+C\\
\int(x+1)^2dx&=\int(x^2+2x+1)dx=\frac13x^3+x^2+x+C
\end{align*}
の結果が異なるように見えるという点があります。上の式で$1+C$となるところを$C'$のように書き換えれば下の式に一致する、という説明が一般的ですが、$C$が実数全体の集合であると考えることによっても説明できます(本質的には同じことですが)。即ち、
\begin{align*}
\frac13(x+1)^3+C&=\frac13(x+1)^3+\mathbb R\\
&=\left\{\frac13(x+1)^3+c\,\middle|\,c\in\mathbb R\right\}
\\
&=\left\{\frac13x^3+x^2+x+c\,\middle|\,c\in\mathbb R\right\}
\\
&=\frac13x^3+x^2+x+C
\end{align*}
です。次の例も躓きがちなポイントかと思います。
\begin{align*}
I&=\int e^x\sin x=e^x\sin x-\int e^x\cos xdx\\
&=e^x\sin x-e^x\cos x-\int e^x\sin xdx\\
&=e^x\sin x-e^x\cos x-I\\
\therefore2I&=e^x\sin x-e^x\cos x+{\color{red}C}
\end{align*}
どこからともなく$C$が出てきました。普通に考えると、$I=e^x\sin x-e^x\cos x-I$が成り立つような$I$は$\dfrac12(e^x\sin x-e^x\cos x)$しかないように思えます。しかし、$I$が集合であればそうとも限りません。$e^x\sin x$の原始函数の1つを$f(x)$とすると、$I=f(x)+\mathbb R$なので
\begin{align*}
e^x\sin x-e^x\cos x-I&=\{e^x\sin x-e^x\cos x-f(x)-c\mid c\in\mathbb R\}\\
&=\{e^x\sin x-e^x\cos x-f(x)+c\mid c\in\mathbb R\}
\end{align*}
これが$I$に等しいことから、任意に$f(x)+c_1\in I$をとると
$$ f(x)+c_1=e^x\sin x-e^x\cos x-f(x)+c_2(\in e^x\sin x-e^x\cos x-I)$$
を満たす$c_2$が存在します。両辺に$f(x)+c_1$を足せば
$$2(f(x)+c_1)=e^x\sin x-e^x\cos x+(c_1+c_2)$$
を得ます。これは、$2I$の任意の要素が$e^x\sin x-e^x\cos x+\mathbb R$に属することを表しています。逆に、$e^x\sin x-e^x\cos x+\mathbb R$の任意の要素が$2I$に属することも同様に分かります。以上より、
$$2I=e^x\sin x-e^x\cos x+\mathbb R$$
が分かりました。これら2つの具体例から分かるように、積分定数と呼ばれる「$C$」は実数全体の集合であると考えるのがよさそうです。
…本当にそれで良かったのでしょうか？
「公式」は本当に正しいか
数学Ⅲで習う積分公式として、次のものがあります。
$$\int\frac1xdx=\log|x|+C$$
定数$c$を用いて$\log|x|+c$と表される函数を$x$で微分すると$x<0$でも$0< x$でも$\dfrac1x$に等しくなるので、この公式は正しそうに思えるかもしれません。ですがよく考えてみましょう。不定積分とは原始函数全体でなければならないはずです。しかし、実際のところ$\dfrac1x$の原始函数は$\log|x|+c$の形のものだけではありません。例えば
$$ f(x)=\begin{cases}\log|x|&(x<0)\\\log|x|+1&(0< x)\end{cases}$$
と表される函数を考えると、これは$x\neq0$で微分可能であって導函数は$\dfrac1x$に一致します。つまり$f(x)$も$\dfrac1x$の原始函数なのですが、$f(x)=\log|x|+c$の形に表すことはできません。ではなぜこのような正しくない公式が流布しているのでしょうか。ここにはおそらく次の定理が関わっていると思われます。
実数全体で定義された函数$f(x),F(x)$が$f(x)=F'(x)$を満たすとする。このとき$f(x)$の原始函数は、定数$c$を用いて$F(x)+c$と表せる。
$F(x)+c$の形の函数が$f(x)$の原始函数であることは簡単に分かるので、$f(x)$の原始函数がすべて$F(x)+c$の形に書けることを言えばよい。
$F_0(x)$を$f(x)$の原始函数とし、$g(x)=F_0(x)-F(x)$とおく。平均値の定理から、任意の実数$\alpha,\beta$ ($\alpha<\beta$)に対して
$$\frac{g(\alpha)-g(\beta)}{\alpha-\beta}=g'(\gamma)$$
を満たす実数$\gamma$ ($\alpha<\gamma<\beta$)が存在する。ここで、
$$ g'(c)=F_0'(\gamma)-F'(\gamma)=f(\gamma)-f(\gamma)=0$$
であるので$g(\alpha)=g(\beta)$である。以上より定数$c$を用いて$g(x)=c$と表せて、このとき$F_0(x)=F(x)+c$である。
この定理では$f(x)$が実数全体で定義されていることを仮定しています。定義域が実数全体でないような函数の場合、$\alpha$と$\beta$の選び方によっては$\alpha\leqq x\leqq\beta$の範囲で$f(x)$が定義されているとは限りません。そのため平均値の定理が適用できず、最終的な結論が成り立つとは言えません。
積分定数は定数ではない？
では、$f(x)$の原始函数の1つが与えられたとき、$f(x)$の原始函数を全て求めるにはどうすればよいでしょうか。以下の定理が答えになります。
$D$を実数全体の集合の部分集合とし、$D$を定義域とする函数$f(x),F(x)$が$f(x)=F'(x)$を満たすとする。このとき
$$\int f(x)dx=F(x)+C(D)$$
ただし、$C(D)$は$D$上の局所定数函数全体の集合である。
ここで、局所定数函数の定義は下記の通りです。また、$D$が閉区間($a\leqq x\leqq b$の形の区間)だったり有理数全体の集合だったりするとうまく微分できないので、そのようなものは考えないことにします。大学数学の言葉を使って言えば、定理2における$D$は開集合のみを考えるということです。
$D$を実数全体の集合の部分集合とする。$D$を定義域とする函数$f(x)$が局所定数函数であるとは、
$$ I=\{x\mid a\leqq x\leqq b\}\subset D$$
の形の任意の区間$I$に対して$f(x)$が$I$上定数函数となることをいう。
ややこしい説明に感じるかもしれませんが、下図のようなグラフをもつ函数が局所定数函数です。
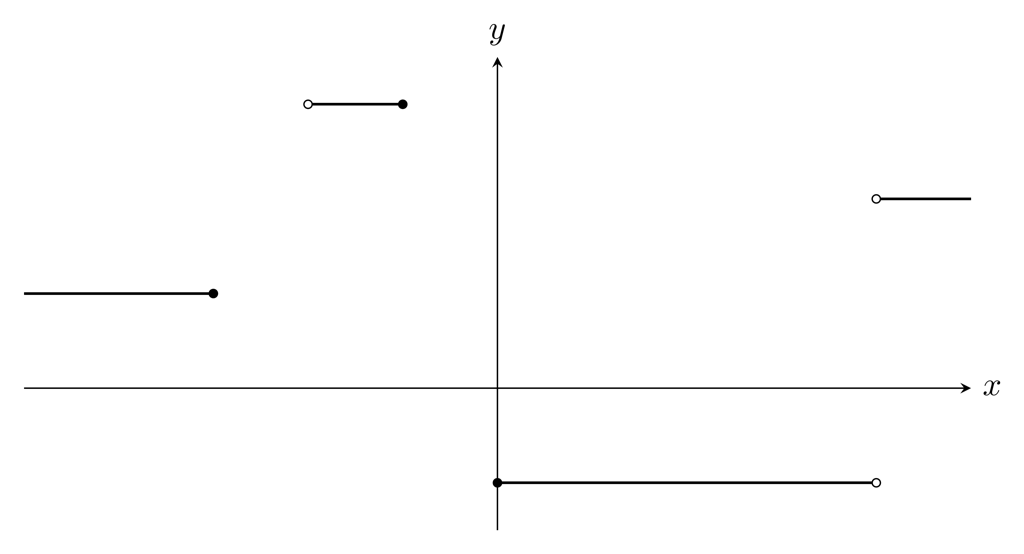局所定数函数
例えば$x\neq\pm1$で次のように定義された$f(x)$を考えます。
$$ f(x)=\begin{cases}1&(|x|<1)\\3&(1<|x|)\end{cases}$$
$f(x)$の定義域は$x\lt-1,\,-1\lt x\lt1,\,1\lt x$の3つに分かれます。これらの各区間において$f(x)$は定数函数ですから、$f(x)$は局所定数函数であると言えます。一方、実数$x$の整数部分を$\lfloor x\rfloor$と書くとき、実数全体で定義された函数$f(x)=\lfloor x\rfloor$は局所定数函数ではありません。なぜなら、$0\leqq x\leqq2$は定義域に含まれますがこの範囲で$f(x)$は定数函数ではないからです。
定理2も定理1と同様の流れで示せます。
$g(x)\in C(D)$を用いて$F(x)+g(x)$と書ける函数が$f(x)$の原始函数であることは簡単に分かるので、$f(x)$の原始函数がすべてこの形に書けることを言えばよい。
$\{x\mid a\leqq x\leqq b\}\subset D$を満たすように実数$a,b$をとり、左辺の集合を$I$とする。$F_0(x)$を$f(x)$の原始函数とし、$g(x)=F_0(x)-F(x)$とおく。平均値の定理から、任意の$\alpha,\beta\in I$ ($\alpha<\beta$)に対し
$$\frac{g(\alpha)-g(\beta)}{\alpha-\beta}=g'(\gamma)$$
を満たす実数$\gamma$ ($\alpha<\gamma<\beta$)が存在する。ここで、
$$ g'(\gamma)=F_0'(\gamma)-F'(\gamma)=f(\gamma)-f(\gamma)=0$$
であるので$g(\alpha)=g(\beta)$である。以上より$g(x)$は$I$上で定数函数である。よって$g(x)$は$D$上の局所定数函数であって$F_0(x)=F(x)+g(x)$なので、示したかった命題が得られる。
定理2において、$C(D)$を$C$と略記すれば式の形は一般的なものと一致します。このことから、「積分定数」と呼ばれているものを定数でも実数全体の集合でもなく局所定数函数全体の集合と解釈することで、不定積分に関する種々の公式が正しくなります。これ以外にもよい解釈があるかもしれませんが、とりあえず現時点で私が考える「積分定数とは何か？」に対する最良の答えは「被積分函数の定義域上の局所定数函数全体の集合」です。
余談
微分して$\dfrac1x$になる函数は、実函数(実数を受け実数を返す函数)の意味で言えば前述の通り$\log|x|+c$ ($c$は定数)の形に限られず、
$$ f(x)=\begin{cases}\log|x|+c_1&(x<0)\\\log|x|+c_2&(0< x)\end{cases}$$
という形のものがあります。一方、複素函数(複素数を受け複素数を返す函数)だと事情が異なります。複素函数の意味での微分は実函数の意味での微分とは似て非なるものであり、$\log|x|$は$x$に依らず微分不可能です。そして$\log x+c$ ($c$は定数)の形の函数は$0$でない複素数全体で定義されて導函数が$\dfrac1x$に等しく、かつこれ以外に導函数が$\dfrac1x$に等しくなるような函数はありません。正確に言えば、どの複素数$x_0$に対しても適切な主値の取り方をすることにより$x=x_0$で$\log x+c$は複素微分可能となります。この意味でも
$$\int\frac1xdx=\log|x|+C$$
($C$は定数)という書き方はよくないと思うわけです。
この記事を高評価した人
この記事に送られたバッジ
投稿者
