エレファント数学① ~カプレカ操作~
エレファントな証明
以下の定理をご存じだろうか。
平面上のいかなる地図も、隣接する領域が異なる色になるように塗り分けるには4色あれば十分である。
かつて未解決だったころは四色問題として名を馳せていたものである。1976年にケネス・アッペルとヴォルフガング・ハーケンによって、コンピュータを用いる総当たり的手法で反例がないことを示す証明が成された。当時はプログラムの複雑さなどの様々な理由から否定的な見方をされていたが、その後改良を加えより簡易なアルゴリズムで再証明が成され、現在では四色問題は解決されているとされている。
クリシェだが、簡潔で美しい証明方法をエレガントな証明というのに対し、このようなある種の「ごり押し」の証明方法を"エレファント"な証明と揶揄されることがある。
そこで、ここではもっと簡単な問題に対して、エレファントな解答を与えていくこととする。
エレファント数学
カプレカ数(Kaprekar number)
カプレカ数とは以下のような数のことである。
各桁を並べ替えて最大にした数と最小にした数の差が元の数に等しくなるような整数をカプレカ数という。
また、「各桁を並べ替えて最大にした数と最小にした数の差を取る」操作をカプレカ操作と呼ぶことがある。(以後単に操作という)
カプレカ数の例に495や6174がある。2数それぞれ操作を行うと
7641-1467=6174
954-459=495
となり、定義に従う。(※0もこの定義ではカプレカ数である。)
この操作に対して次の問題を考える。
いかなる5桁の正の整数も、有限回の操作のうちに4回以下の循環に入ることを示せ。
n回の循環というのは、n回操作を行うと元の整数に戻るという意味である。つまりn=1のときの整数を特にカプレカ数という。
これを一般的な証明をするのであれば、任意の5桁の正の整数を上手く表して、それに対して操作を何回か行い、ある4回以下の循環に入ることを示すこととなるだろう。しかし、実際にやってみると簡単には上手くいかないことがわかる。
しかし、今回議論されている数は、10000から99999までの高々90000個である。有限ならエレファント数学の考察対象だ。
Let's elephant
pythonで以下のプログラムを実行する。
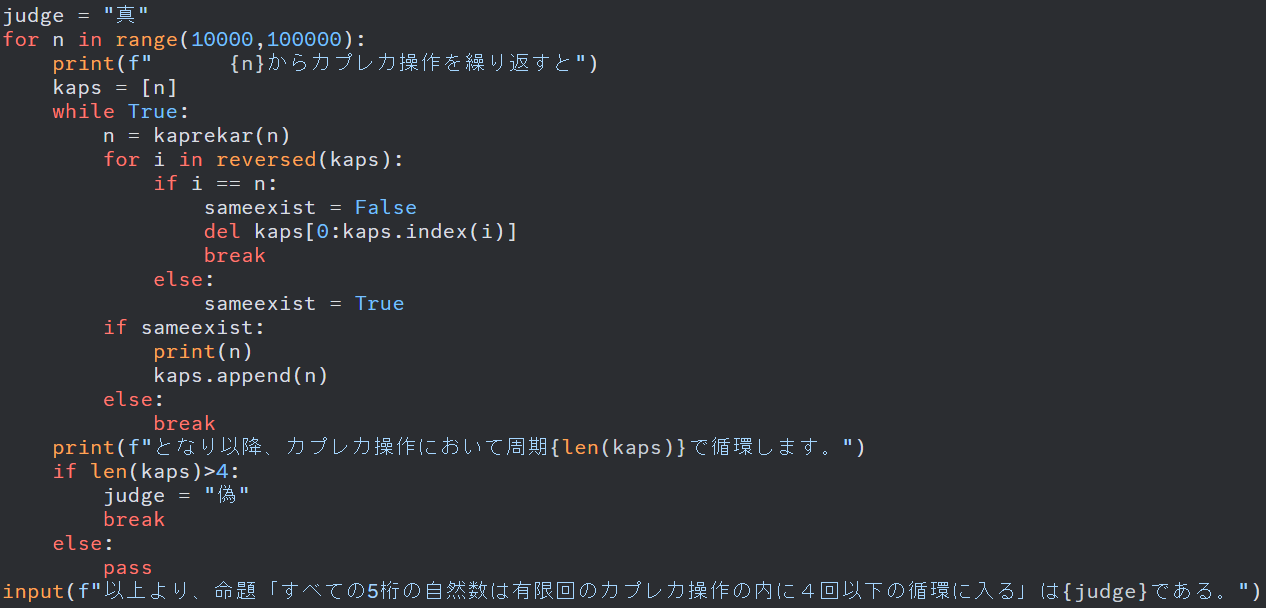 実行するプログラム
実行するプログラム
(kaprekar(n)はnに対して操作を行ったもの(文字列)を戻り値とする関数として別途書いている。)
これを実行すると10000から99999まで順に検証を行い、満たさないものが一つでもあれば"偽"が、すべて満たせば"真"がjudgeに代入されて最後のinputが出力される。
実行結果は"真"となる。よって題意は示された。
(実行の様子は私のTwitter(現X)にあげているので興味があればご確認ください)
カプレカ操作のプログラム(例)
参考になれば
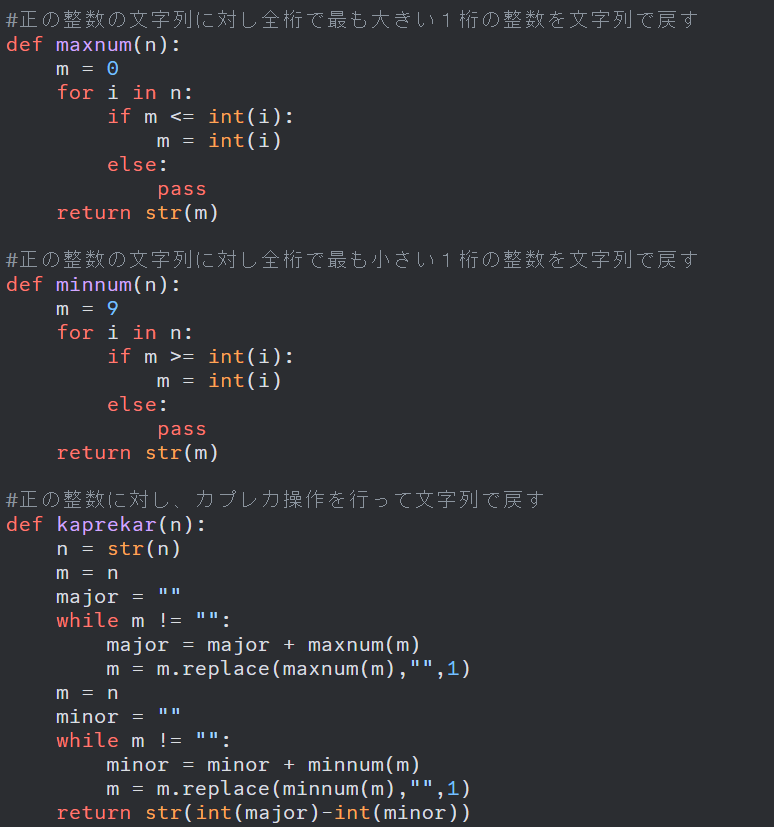 カプレカ操作
カプレカ操作
