AIME 2024 日本語訳

ayaは毎朝$9km$歩いて喫茶店に着きます．ある日，彼女は時速$skm$で歩き，喫茶店での$t$分を含めて計$4$時間かかりました．別の朝，彼女は時速$s+2km$で歩き，喫茶店での$t$分を含めて計$2$時間$24$分かかりました．今朝，彼女は$s+\dfrac{1}{2}km$で歩くとすると，喫茶店での$t$分を含めて計何分かかりますか？

実数$x,y\gt 1$は$\log_x(y^x)=\log_y(x^{4y})=10$を満たします．$xy$の値を求めてください．

AliceとBobがゲームを行います．はじめに$n$個の石の山があり，Aliceを先手として交互に$1$個または$4$個の石を山から取り除きます．最後の石を取り除いた方が勝ちです．
Aliceの行動にかかわらず，Bobが必ず勝てるような$2024$以下の$n$の個数を求めてください．

Jenは${1,2,\cdots ,10}$から$4$数を選び，抽選機も同じように$4$数を選ぶ．Jenの選んだ数のうち少なくとも$2$つを抽選機が選ぶと，Jenは賞を取る．Jenの選んだ$4$数すべてを抽選機が選ぶと，Jenは大賞を取る．Jenが賞を取ったときの，Jenが大賞を取る条件付き確率は互いに素な正整数$m,n$を用いて$\dfrac{m}{n}$と表せるので$m+n$を求めてください．

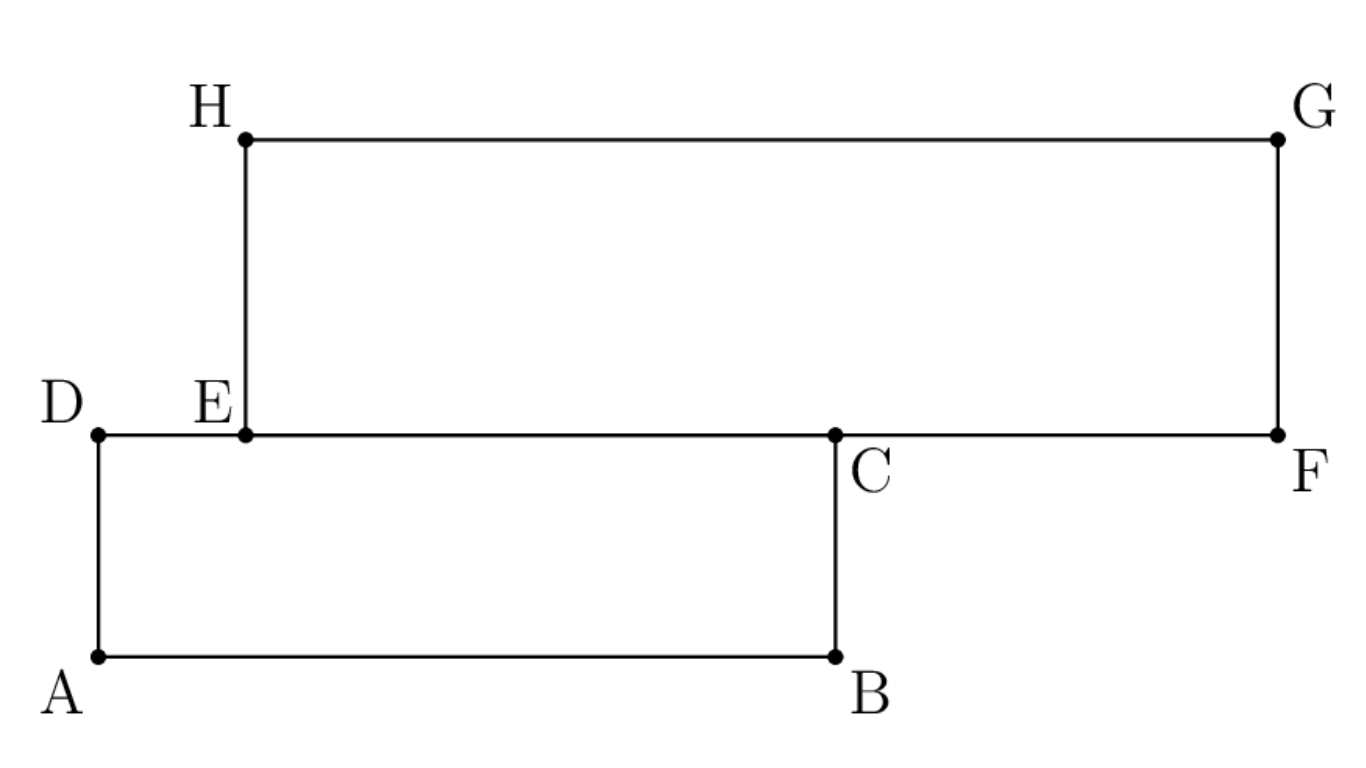
長方形$ABCD,EFGH$が$D,E,C,F$がこの順に一直線に並ぶように描かれている．$A,D,H,G$が共円であり，$BC=16,AB=107,FG=17,EF=184$であるとき，$CE$の長さを求めてください．

$8\times 8$のマス目の線上を通って左下から右上に行く長さ$16$の経路であって，ちょうど$4$回曲がるものはいくつありますか？

$z$が$|z|=4$を満たす複素数であるとき
$$(75+117i)z+\dfrac{96+144i}{z}$$
の実部の最大値を求めてください．

半径が$34$である$8$個の円が$\triangle ABC$の辺$BC$に接しており，$1$つめの円は辺$AB$に接し，以降の円は一つ前の円に接し，最後の円は辺$AC$に接している．同じように，半径が$1$である$2024$個の円が辺$BC$上に置かれている．$\triangle ABC$の内接円の半径は互いに素な正整数$m,n$を用いて$\dfrac{m}{n}$と表せるので，$m+n$を求めてください．

双曲線$\dfrac{x^2}{20}-\dfrac{y^2}{24}=1$上に四点$A,B,C,D$があり，四角形$ABCD$は中心が原点であるひし形をなしている．$BD^2$未満の最大の実数を求めてください．

$AB=5,BC=9,CA=10$である$\triangle ABC$がある．$\triangle ABC$の外接円の$B$と$C$における接線の交点を$D$とし，$AD$と$\triangle ABC$の外接円の交点を$P\not= A$とする．$AP$の長さは互いに素な正整数$m,n$を用いて$\dfrac{m}{n}$と表せるので$m+n$を求めてください．

正八角形の各頂点が赤色または青色に等しい確率で塗られている．適切に回転したとき，すべての青色の頂点が元あった赤色の頂点上にくるようにできる確率は互いに素な正整数$m,n$を用いて$\dfrac{m}{n}$と表せるので$m+n$を求めてください．

$f(x)=||x|-\dfrac{1}{2}|,g(x)=||x|-\dfrac{1}{4}|$とする．以下のグラフの交点の個数を求めてください．
$y=4g(f(sin(2\pi x))),x=4g(f(cos(3\pi y)))$

$n^4+1$が$p^2$で割り切れるような正整数$n$が存在するような最小の素数を$p$とする．$m^4+1$が$p^2$で割り切れるような最小の正整数$m$を求めてください．

四面体$ABCD$は$AB=CD=\sqrt{41},AC=BD=\sqrt{80},BC=AD=\sqrt{89}$を満たす．四面体の全ての面からの距離が等しいような点$I$が四面体の内部に存在し，$I$と四面体の面との距離は互いに素な正整数$m,p$と平方因子を持たない正整数$n$を用いて$\dfrac{m\sqrt{n}}{p}$と表せるので，$m+n+p$を求めてください．

体積が$23$，表面積が$54$の直方体の集合を$\mathcal{B}$とし，$\mathcal{B}$のいずれの要素も完全に内部に入る(表面上を含む)ような球の半径の最小値を$r$とする．$r^2$は互いに素な正整数$p,q$を用いて$\dfrac{p}{q}$と表せるので$p+q$を求めてください．