円にできる影の長さが一定になる光源の軌跡

問題：x軸の上に$x^2 + (y-1)^2 = 1$の円がある.点光源$L$から発せられた光が$x$軸上に作る影の長さが一定となるような点光源$L$の軌跡は何か?

画像の名前

解答:双曲線になる.
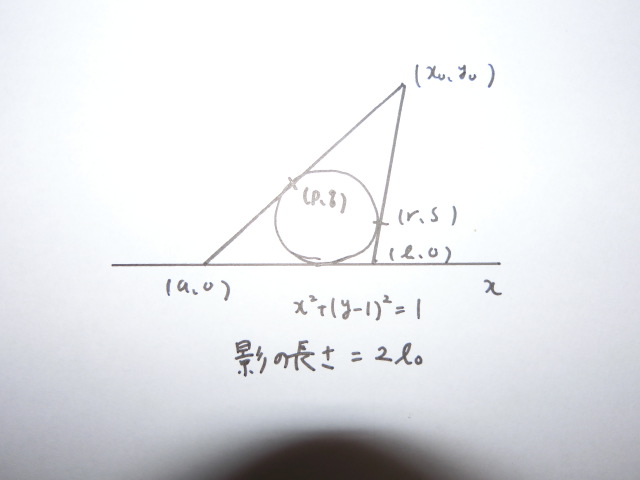
図のように接点$(p,q),(r,s)$,$x$軸上にできる影の両端$(a,0),(b,0)$を取る.

$(p,q)$を通る接線の方程式は$px+(q-1)(y-1) = 1$である.これが点$(a,0)$を通るので
$pa + (q-1)(-1) = 1$
従って
$q = pa$.
またこの直線上に点$(p,q)$があるので
$p^2 + (q-1)^2 = 1$
$q = pa$と合わせて$p \neq 0$であることを使うと
$p = \frac{2a}{a^2+1}$

同様に
$s = rb, r = \frac{2b}{b^2+1}$が分かる.

点光源$L$の座標を$(x_0,y_0)$とするとこれは二つの直線
$px + (q-1)(y-1) = 1, rx + (s-1)(y-1) = 1$の交点なので
$x_0 = \frac{s-q}{qr-ps + p-r}$
$y_0 = \frac{qr-ps}{sp-qr + r-p}$
となる.

これに$q = pa,s = rb$を代入し$q,s$を消去し,さらに$p = \frac{2a}{a^2+1},r = \frac{2b}{b^2+1}$を使うと
$x_0 = \frac{a+b}{ab+1}$
$y_0 = \frac{2ab}{ab+1}$
となる.

$(a,0),(b,0)$の中点のx座標を$t$,影の長さを$2l_0$とすると$l_0 > 1$で
$a = t - l_0,b = t + l_0$となる.これを上の$y_0$の式に代入すると
$y_0 = 2 - \frac{2}{ab+1} $
整理して
$t^2 = l_0^2 - 1 + \frac{2}{2-y_0}$が得られる.また
$\frac{2}{ab+1} = 2 - y_0$であり,$x^2 = \frac{4t^2}{(ab+1)^2}$であるから
$x^2 = (2-y_0)^2 \{l_0^2 - 1 + \frac{2}{2-y_0} \}$
すなわち
$x^2 = (l_0^2-1)(y_0 - 2)^2 - 2(y_0 -2)$
となりこれは平方完成をすることで双曲線の方程式となる.(解答終わり)

座標を使わず,初等幾何的に解けたという方はコメントをお願いします.