２日目

見た目が美しくない積分を作ったので紹介します。$$\begin{array}{r}{\int }_{\pi /4}^{\pi /2}\frac{{\cos }^2(2\theta )}{{\sin }^{10}(\theta )\ln (\tan \left(\theta \right))}d\theta =2\ln \left(\frac{5}{3}\right)\end{array}$$

Desmos上で数値的に計算したら、大体あってますね。Wolfram Alphaに投げても数値しか返さなかったので、厳密に正しいかは知りません。
一見すると、三角関数があるので、$t=\tan \left(\frac{\theta }{2}\right)$で有理型関数に帰着できそうですが、分母の$\ln (\tan \left(\theta \right))$がそれを阻んでいます。かつて自分が残した殴り書きのメモを参照しながら、なるべくわかりやすく導出していきます。

$\ln (1+x)$の別表現

まず、${\displaystyle {\int }_0^1\frac{t^x-1}{\ln \left(t\right)}dt=\ln (1+x)}$であることを示します。
$$\begin{array}{rl}& I(x)={\int }_0^1\frac{t^x-1}{\ln \left(t\right)}dtとします。\\ & ライプニッツの積分法則(またはファインマンの手法)より、\\ & \frac{dI}{dx}={\int }_0^1\frac{\partial }{\partial x}(\frac{t^x-1}{\ln \left(t\right)})dt={\int }_0^1\frac{t^x\ln \left(t\right)}{\ln \left(t\right)}dt={\int }_0^1{t}^{x}dt\\ & =\frac{1}{x+1}\\ & よって、\\ & I^{\prime }(x)=\frac{1}{x+1}\\ & ですから、両辺を積分して、\\ & I(x)=\ln (x+1)+C(Cは積分定数)\\ & ここで、x=0をI(x)に代入すると、\\ & I(0)={\int }_0^1\frac{t^0-1}{\ln \left(t\right)}dt={\int }_0^1\frac{1-1}{\ln \left(t\right)}dt=0\\ & です。よって、先ほど導出した式にx=0を代入して、\\ & 0=\ln (0+1)+C\\ & \therefore C=0\end{array}$$
これで、${\displaystyle {\int }_0^1\frac{t^x-1}{\ln \left(t\right)}dt=\ln (1+x)}$が示されました。

さて、この積分について、$t=\frac{1}{u}$と置換し、$u$を$t$と置きなおすと、いろいろと計算して、
${\displaystyle {\int }_1^{\mathrm{\infty }}\frac{t^x-1}{t^{x+2}\ln \left(t\right)}dt=\ln (1+x)}$となります。これで今回の定積分を導出するための道具は揃いました。

雑多な作業

ここから$J(x)={\displaystyle {\int }_1^{\mathrm{\infty }}\frac{t^x-1}{t^{x+2}\ln \left(t\right)}dt}$と定義します。先ほど導出したことから、$J(x)=\ln (x+1)$です。また、$I(x)={\displaystyle {\int }_0^1\frac{t^x-1}{\ln \left(t\right)}dt=\ln (x+1)}$であるので、$I(x)=J(x)$です。
$I(x)にx=4$を代入して、$I(4)={\displaystyle {\int }_0^1\frac{t^4-1}{\ln \left(t\right)}dt=\ln \left(5\right)}$です。これを$A$とします。
${\displaystyle A={\int }_0^1\frac{(t-1)(t+1)(t^2+1)}{\ln \left(t\right)}dt}$
$t=1-u$と置換し、$u$を$t$に置きなおします。

${\displaystyle ={\int }_0^1\frac{-t(2-t)(2-2t+t^2)}{\ln (1-t)}dt}$

${\displaystyle =-{\int }_0^1\frac{(t^2-2t{)}^2}{\ln \left(\frac{1}{1-t}\right)}dt+2{\int }_0^1\frac{t(2-t)}{\ln \left(\frac{1}{1-t}\right)}dt}$
ここで、$\frac{1}{1-t}=u$と置換します。$dt=\frac{du}{u^2}$で、積分範囲は$t:0\to 1$で$u:1\to \mathrm{\infty }$です。

${\displaystyle =-{\int }_1^{\mathrm{\infty }}\frac{{({(1-\frac{1}{u})}^2-2(1-\frac{1}{u}))}^2}{\ln \left(u\right)}\cdot \frac{1}{u^2}du+2{\int }_1^{\mathrm{\infty }}\frac{(1-\frac{1}{u})(1+\frac{1}{u})}{\ln \left(u\right)}\cdot \frac{1}{u^2}du}$

${\displaystyle =-{\int }_1^{\mathrm{\infty }}\frac{{(\frac{1}{u^2}-1)}^2}{u^2\ln \left(u\right)}du+2{\int }_1^{\mathrm{\infty }}\frac{(1-\frac{1}{u^2})}{u^2\ln \left(u\right)}du}$

${\displaystyle =-{\int }_1^{\mathrm{\infty }}\frac{{(u^2-1)}^2}{u^6\ln \left(u\right)}du+2{\int }_1^{\mathrm{\infty }}\frac{u^2-1}{u^4\ln \left(u\right)}du}$
ここで、第2項めの${\displaystyle {\int }_1^{\mathrm{\infty }}\frac{u^2-1}{u^4\ln \left(u\right)}du}$は、$J(x)$に$x=2$を入れたものに等しいです。よって、

${\displaystyle {\int }_1^{\mathrm{\infty }}\frac{u^2-1}{u^4\ln \left(u\right)}du=\ln \left(3\right)}$

です。すなわち、

${\displaystyle A=-{\int }_1^{\mathrm{\infty }}\frac{{(u^2-1)}^2}{u^6\ln \left(u\right)}du+2\ln \left(2\right)}$

ですが、もともと$A=I(4)=\ln \left(5\right)$ですから、移項して、
${\displaystyle {\int }_1^{\mathrm{\infty }}\frac{{(u^2-1)}^2}{u^6\ln \left(u\right)}du=\ln \left(\frac{9}{5}\right)\cdots \mathrm{①}}$

が成り立ちます。これを$B$と名付けましょう。

次に、${\displaystyle I\left(8\right)={\int }_0^1\frac{t^8-1}{\ln t}dt}$を用意します。$C$と名付けます。$C=\ln \left(9\right)$です。
${\displaystyle C={\int }_0^1\frac{(t^4+1)(t^2+1)(t+1)(t-1)}{\ln t}dt}$
先ほどと同様に$t=1-u$と置換し、 $u$を$t$と置きなおして、
${\displaystyle ={\int }_0^1\frac{\{{(1-t)}^4+1\}(t^2-2t+2)(t^2-2t)}{\ln (1-t)}dt}$
簡略化のために、$T=t^2-2t$とすると、
${\displaystyle ={\int }_0^1\frac{(T^2+2T+2)(T^2+2T)}{\ln (1-t)}dt}$

${\displaystyle ={\int }_0^1\frac{{(T^2+2T)}^2+2(T^2+2T)}{\ln (1-t)}dt}$

${\displaystyle ={\int }_0^1\frac{{(t^2-2t)}^2{(t^2-2t+2)}^2}{\ln (1-t)}dt+2{\int }_0^1\frac{{(t^2-2t)}^2}{\ln (1-t)}dt+4{\int }_0^1\frac{t^2-2t}{\ln (1-t)}dt}$
左の積分から順に$C_1,C_2,C_3$とします。$C_1+2C_2+4C_3=C$です。それぞれの値を計算しましょう。

$C_2$の計算

${\displaystyle C_2={\int }_0^1\frac{{(t^2-2t)}^2}{\ln (1-t)}dt}$
例にもれず、$\frac{1}{1-t}=u$と置換します。すると、
${\displaystyle ={\int }_1^{\mathrm{\infty }}\frac{{\{{(1-\frac{1}{u})}^2-2(1-\frac{1}{u})\}}^2}{\ln \left(\frac{1}{u}\right)}\cdot \frac{1}{u^2}du}$

=${\displaystyle {\int }_1^{\mathrm{\infty }}-\frac{{(1-\frac{1}{u})}^2{((1-\frac{1}{u})-2)}^2}{u^2\ln \left(u\right)}du}$

=${\displaystyle {\int }_1^{\mathrm{\infty }}-\frac{{(1-\frac{1}{u})}^2{(1+\frac{1}{u})}^2}{u^2\ln \left(u\right)}du={\int }_1^{\mathrm{\infty }}-\frac{{(1-\frac{1}{u^2})}^2}{u^2\ln \left(u\right)}du}$

${\displaystyle =-{\int }_1^{\mathrm{\infty }}\frac{{(u^2-1)}^2}{u^6\ln \left(u\right)}du}$
見覚えのある形が出てきましたね。これは先ほどの計算で導出した、$B$の符号が逆転したものです。すなわち、$C_2=-B=-\ln \left(\frac{9}{5}\right)$です。

$C_3$の計算

ここまでくればあともう少しです。
${\displaystyle C_3={\int }_0^1\frac{t^2-2t}{\ln (1-t)}dt}$を計算していきます。同様に、$\frac{1}{1-t}=u$と置換します。
${\displaystyle C_3={\int }_1^{\mathrm{\infty }}\frac{{(1-\frac{1}{u})}^2-2(1-\frac{1}{u})}{-\ln \left(u\right)}\cdot \frac{1}{u^2}du}$

${\displaystyle ={\int }_1^{\mathrm{\infty }}\frac{(1-\frac{1}{u})(1-\frac{1}{u}-2)}{-u^2\ln \left(u\right)}du={\int }_1^{\mathrm{\infty }}\frac{(1-\frac{1}{u})(1+\frac{1}{u})}{u^2\ln \left(u\right)}du={\int }_1^{\mathrm{\infty }}\frac{(1-\frac{1}{u^2})}{u^2\ln \left(u\right)}}$

${\displaystyle ={\int }_1^{\mathrm{\infty }}\frac{u^2-1}{u^4\ln \left(u\right)}}$
となりますが、これは$J(x)$に$x=2$を代入したものに等しく、すなわち$C_3=J(2)=\ln \left(3\right)$です。

$C_1$の計算

計算というか、先ほど導出した者たちを使ってシンプルに表します。
$C=C_1+2C_2+4C_3$でしたから、
$C_1=C-2C_2-4C_3$
$=\ln \left(9\right)-2(-\ln \left(\frac{9}{5}\right))-4(\ln \left(3\right))$
$=\ln \left(9\right)+2\ln \left(9\right)+2\ln \left(\frac{1}{5}\right)-2\ln \left(9\right)=2\ln \left(\frac{3}{5}\right)$
よって、
${\displaystyle C_1={\int }_0^1\frac{{(t^2-2t)}^2{(t^2-2t+2)}^2}{\ln (1-t)}dt=2\ln \left(\frac{3}{5}\right)}$です。
さて、勘のいい方は気づかれたかもしれませんが、これは冒頭に示した積分結果の符号が逆転したものです。つまり、この$C_1$を変形して、今回の積分を導出します。

クライマックス

${\displaystyle C_1={\int }_0^1\frac{{(t^2-2t)}^2{(t^2-2t+2)}^2}{\ln (1-t)}dt}$です。これもまた$\frac{1}{1-t}=u$と置換していきます。
${\displaystyle C_1={\int }_1^{\mathrm{\infty }}\frac{{({(1-\frac{1}{u})}^2-2(1-\frac{1}{u}))}^2{({(1-\frac{1}{u})}^2-2(1-\frac{1}{u})+2)}^2}{-\ln \left(u\right)}\cdot \frac{1}{u^2}du}$

${\displaystyle ={\int }_1^{\mathrm{\infty }}\frac{{(\frac{1}{u^2}-1)}^2{(1+\frac{1}{u^2})}^2}{-u^2\ln \left(u\right)}du={\int }_1^{\mathrm{\infty }}\frac{{(1-u^2)}^2{(1+u^2)}^2}{-u^{10}\ln \left(u\right)}du}$

$u=\tan \left(\theta \right)$と置換して、$du=\frac{d\theta }{{\cos }^2(\theta )}$で積分範囲は$u:1\to \mathrm{\infty }$で$\theta :\frac{\pi }{4}\to \frac{\pi }{2}$です。

${\displaystyle ={\int }_{\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{{\left(\frac{\cos \left(2\theta \right)}{{\cos }^2\left(\theta \right)}\right)}^2{\left(\frac{1}{{\cos }^2\left(\theta \right)}\right)}^2}{-{\tan }^{10}\left(\theta \right)\ln (\tan \left(\theta \right))}\cdot \frac{1}{{\cos }^2\left(\theta \right)}d\theta }$

${\displaystyle =-{\int }_{\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{{\cos }^2\left(2\theta \right)}{{\sin }^{10}\left(\theta \right)\ln (\tan \left(\theta \right))}d\theta }$
これは$C_1$で、$C_1=-2\ln \left(\frac{3}{5}\right)$でしたから、両辺のマイナスを打ち消して、

${\displaystyle {\int }_{\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{{\cos }^2\left(2\theta \right)}{{\sin }^{10}\left(\theta \right)\ln (\tan \left(\theta \right))}d\theta =2\ln \left(\frac{5}{3}\right)}$
が示せました。

最後に

今回の被積分関数の概形は、次のようになります。
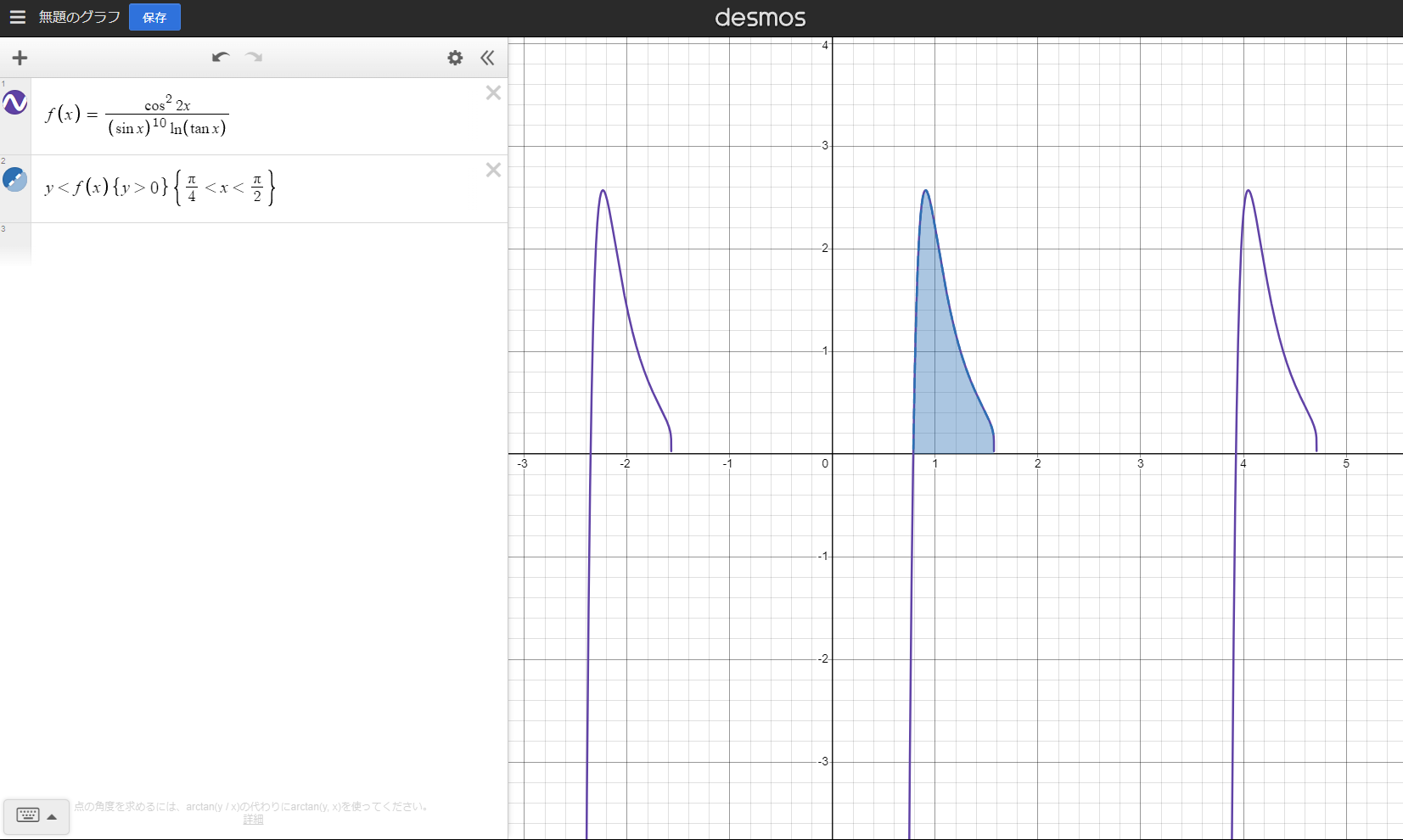
青色の部分の面積が$2\ln \left(\frac{5}{3}\right)$になるというわけですね。先端が尖りすぎているわけでもなく、相手を傷つけずに無効化する護身用グッズにありそうな形です。肋骨の隙間とかに差し込んだら痛そうです。
今回の積分のポイントは、$x^{2n}-1$の因数分解と、同型出現でしょうか。このまま続けていっても更に複雑な積分は生み出せそうですが、計算量に打ちのめされそうなのでやめておきます。お疲れさまでした。