確率漸化式その1〜東大理系第3問(2024)〜

はじめに

受験では, 確率漸化式の問題が頻出である。とくに多角形や多面体のどこかの頂点に点$\mathrm{P}$が止まっていて, そこから辺で繋がっている別の頂点にある確率で移動する問題が多い。これらの問題ではよく推移図という図が用いられる。ただ, 私が知る範囲では, 推移図は受験参考書など受験産業で生み出された資料でしか拝見したことがない。だから, 数学の世界できちんと市民権を得ている（グラフ理論の）グラフを用いて確率漸化式の問題を明解に説明し, それを答案を書く際に役立ててもらおうというのがこの記事の目的である。以下の東大の問題をグラフを使って解くことを今回の目的とします。

グラフ理論のグラフとは

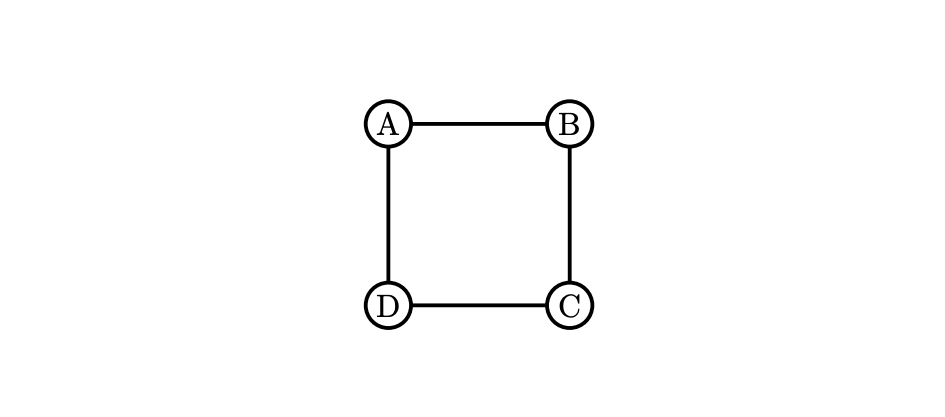グラフの1例

は, 4つの頂点$\mathrm{A, B, C, D}$と4つの辺からなるグラフである。また

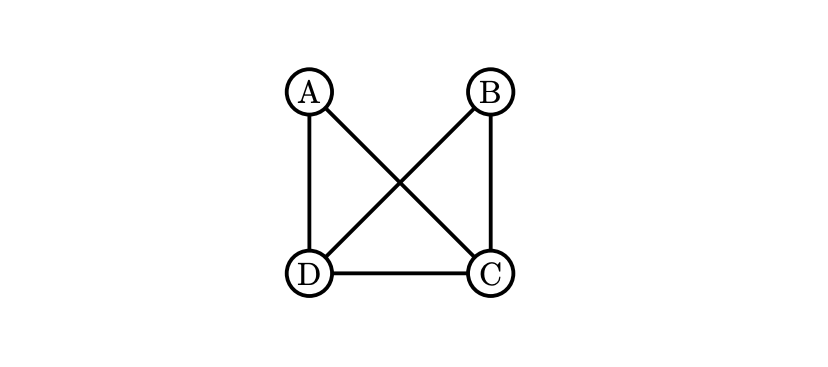グラフの1例

は, 4つの頂点$\mathrm{A, B, C, D}$と5つの辺からなるグラフである。ここで注意してほしいのは, 辺$\mathrm{AC}$と辺$\mathrm{BD}$の交点を頂点としますと宣言しなければ, このグラフの頂点ではない。ゆえに

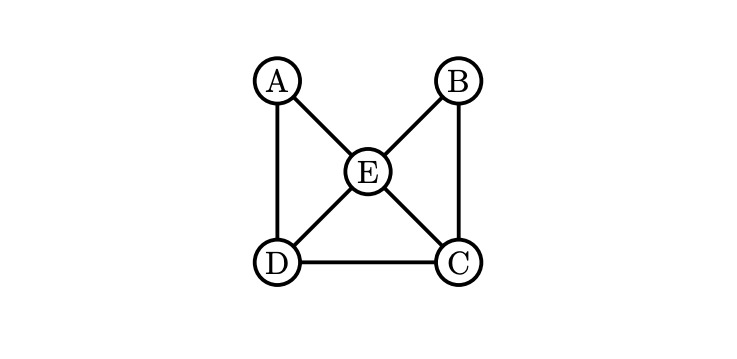グラフの1例

とは, 「異なる」グラフである。このグラフを$G$としよう。しかし, $G$は次のグラフ$G^{\prime}$とは, 「同じ」グラフである。

一般に2つのグラフが「同じ」グラフである。ことをグラフ同型といい次で定義される。

さらにグラフは我々が習ってきた多角形の辺違い辺の端点が同じ頂点である場合もある。今, そのような辺の頂点を$\mathrm{X}$とすると, その辺のことを$\mathrm{X}$を基点とするループという。また, ある2つの頂点を結ぶ辺は複数存在してもよく, そのような辺を多重辺という。しかし今回は幸運にもそのようなものは出ないので例はあげない。

東大理系第3問(2024)をグラフを利用して解く

$(1)\quad $

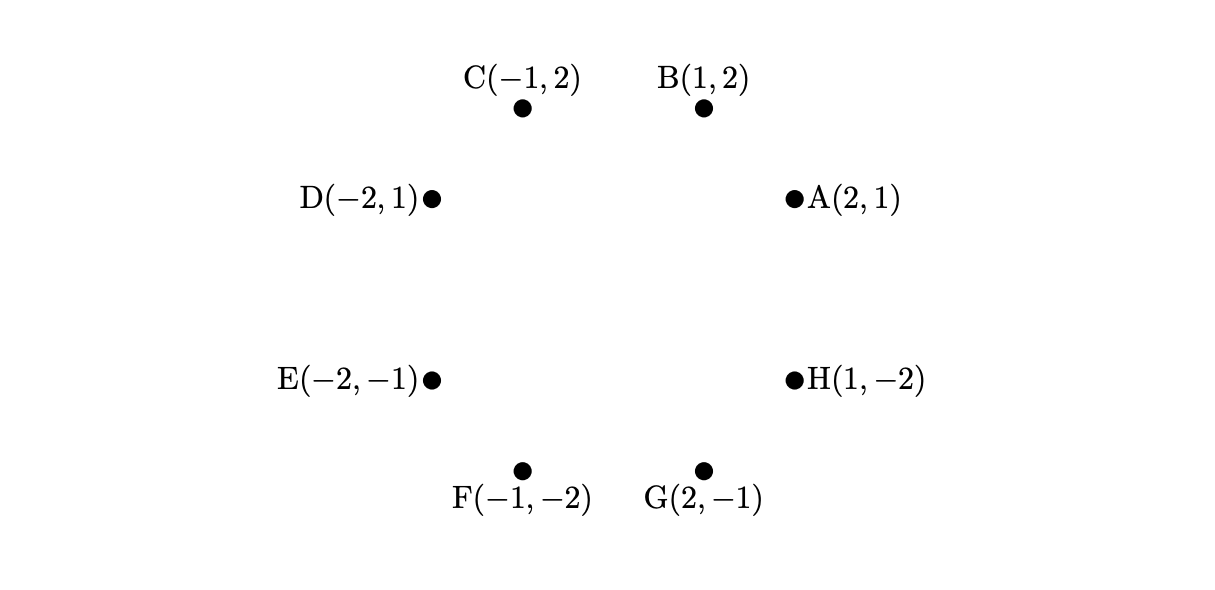(1)の答え

$(2)\quad $
下図をグラフと見てこれを$G$とおく。点$\mathrm{P}$は$G$上でランダムウォークしていると考えることができる。ただし最初$\mathrm{P}$は$\mathrm{A}$にいてある頂点から別の頂点への遷移確率は問題で与えられた確率と同じとする。

グラフ$G$

$G$は原点対称なグラフ$G^{\prime}$と重なった頂点を対応させることで, $G$と$G^{\prime}$はグラフ同型である。またこれら2つのグラフの対応する辺の遷移確率は同じであるから, この$G$の任意の頂点$\mathrm{X}$に対して, $n$秒後に$\mathrm{P}$が$X$にいる確率は, $n$秒後に$\mathrm{P}$がその原点対称な点にいる確率と等しい。よって, $n$秒後に$\mathrm{P}$が$\mathrm{A}$にいる確率と$\mathrm{E}$にいる確率は等しい。

$(3)\quad$ 以下のグラフ$G^{\prime\prime}$上で$\mathrm{P}$がランダムウォークしていると考える。このグラフは有向線分$\mathrm{AB}$を有向線分$\mathrm{FE}$を貼り合わせて（同一視して）$\mathrm{A}$と$\mathrm{F}$が重なった部分を$\mathrm{A}^{\prime}$とし, $\mathrm{B}$と$\mathrm{F}$が重なった部分を$\mathrm{B}^{\prime}$としています。それ以外の点は記号の置き方でアナロジーしてください。

グラフ$G^{\prime\prime}$

ただし, 最初$\mathrm{P}$は$\mathrm{A}^{\prime}$に止まっていて各辺の遷移確率は辺の近くに書いた値である。$n$秒後に$\mathrm{A}^{\prime}, \mathrm{B}^{\prime}, \mathrm{C}^{\prime}, \mathrm{D}^{\prime}$に$\mathrm{P}$がいる確率をそれぞれ$a_{n}, b_{n}, c_{n}, d_{n}$とする。求める確率は, $\dfrac{a_{n}}{2}$なので, $a_{n}$を求める。ここで, ある時刻に$G^{\prime\prime}$の頂点$X$にいるなら, その1秒後には頂点$X$にはいないので, $n$が奇数のとき$a_{n}=c_{n}=0$, $n$が偶数なら$b_{n}=d_{n}=0$が成り立つ。よって, $n=2k$となる$k\in\mathbb{N}$が存在するときのみを考える。$2(k+1)$秒後に$\mathrm{A^{\prime}}$にいる事象は

• $2k, 2(k+1)$秒後ともに$\mathrm{A^{\prime}}$にいる（その確率は$\left(\left(\dfrac{2}{3}\right)^{2}+\left(\dfrac{1}{3}\right)^{2}\right)a_{2k}=\dfrac{5}{9}a_{2k}$）
• $2k$秒後に$\mathrm{D^{\prime}}$にいるが, $2(k+1)$後に$\mathrm{A^{\prime}}$にいる（その確率は$\left(\dfrac{2}{3}\cdot\dfrac{1}{3}+\dfrac{1}{3}\cdot\dfrac{2}{3}\right)a_{2k}=\dfrac{4}{9}d_{2k}$）

の互いに排反な2つの事象の和事象なので
\begin{align*} a_{2(k+1)}=\dfrac{5}{9}a_{2k}+\dfrac{4}{9}d_{2k}. \end{align*}
$a_{2k}+d_{2k}=1$だから
\begin{align*} a_{2(k+1)}-\dfrac{1}{2}=\dfrac{1}{9}\left(a_{2k}-\dfrac{1}{2}\right). \end{align*}
$a_{2}=\dfrac{5}{9}$だから
\begin{align*} a_{2k}=\dfrac{1}{2}\left\{1+\left(\dfrac{1}{9}\right)^{k}\right\}. \end{align*}

\begin{equation*} \therefore\, 求める確率=\left\{\, \begin{aligned} &0\quad (nが奇数)\\ &\dfrac{1}{4}\left\{1+\left(\dfrac{1}{3}\right)^{n}\right\}\quad (nが偶数). \end{aligned} \right. \end{equation*}