PILAME2025-8の一般化について
本記事では京京氏が$X$で出題した$PILAME$杯 問$8$の一般化の個人的な解法を記載していく．元のツイートポストは
こちら
から．
問題を未読の方はまず手を動かして解いてみてほしい．頭痛くなるから．どうやって解くのか初見では闇の中すぎるから．後ほど改めて本記事内でも問題文と解説を記載するので頂点の割り振りなどを覚える必要はないが，何を順に示そうとしているのか咀嚼しやすくするためにもぜひ．
本問題が提唱される元となった$PILAME$杯については
こちら
から情報を確認できる．元の問題自体は過去のコンテストページで $2025$決勝 第$1$部 問$8$.にある．元の問題の段階でかなりの難問なので気をつけられたし．
幾何に限らず代数，整数，組み合わせも含めてクオリティの高い問題が並んでおり，興味のある方はぜひとも取り組んでみていただきたい．ホームページもしっかりしてくださっている運営様，本当にありがとうございます．
それでは一般化の問題について考えていこう．まずは以下の補題を示す．
同一直線上にない$3$点$A,B,C$を通る直角双曲線$\varGamma$上に異なる$2$点$P,Q$を取る．点$P$から直線$AQ,BQ,CQ$に下ろした垂線の脚を順に点$R,S,T$とし，点$Q$から直線$AP,BP,CP$に下ろした垂線の脚を順に点$U,V,W$とする．このとき，直線$RU,SV,TW$は一点で交わる．
なお，点$A$と点$P$が一致するとき直線$AP$は点$A$における$\varGamma$の接線と定義する．
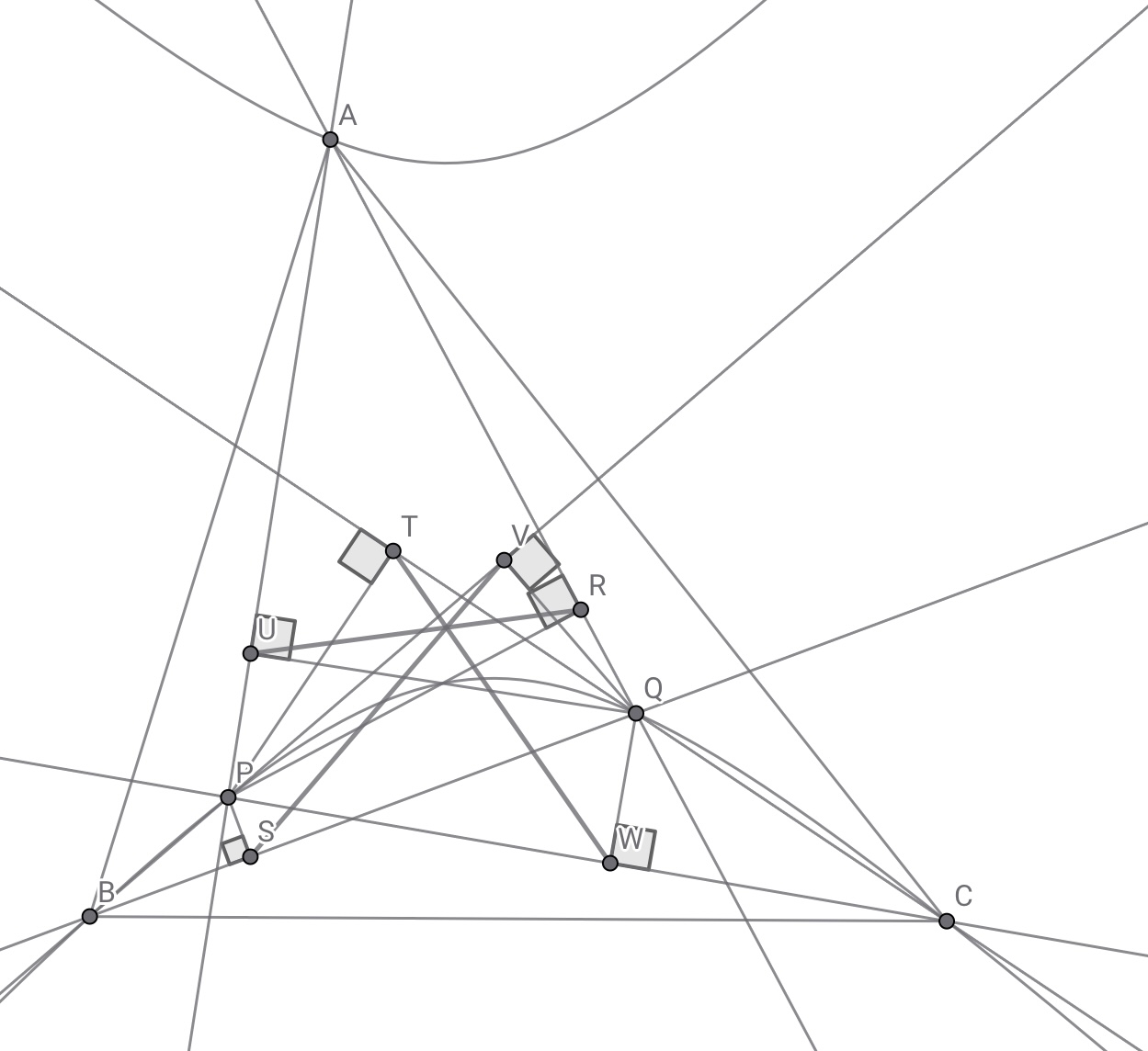垂直が多いということは……
補題を示すにあたって
「直角双曲線上に異なる$3$点$A,B,C$を取ったとき，三角形$ABC$も同一直角双曲線上にある」
と言う性質は前提知識とさせていただく．
$8$点$P,Q,R,S,T,U,V,W$は全て線分$PQ$を直径とする円周上にある．この円を$\varOmega$とする．
直線$PR$と$QU$の交点を点$D$，直線$PS$と$QV$の交点を点$E$，直線$PT$と$QW$の交点を点$F$とする．点$D,E,F$はそれぞれ三角形$APQ,BPQ,CPQ$の垂心となるため全て$\varGamma$上にあり，直線$AD,BE,CF$は全て直線$PQ$に垂直である．
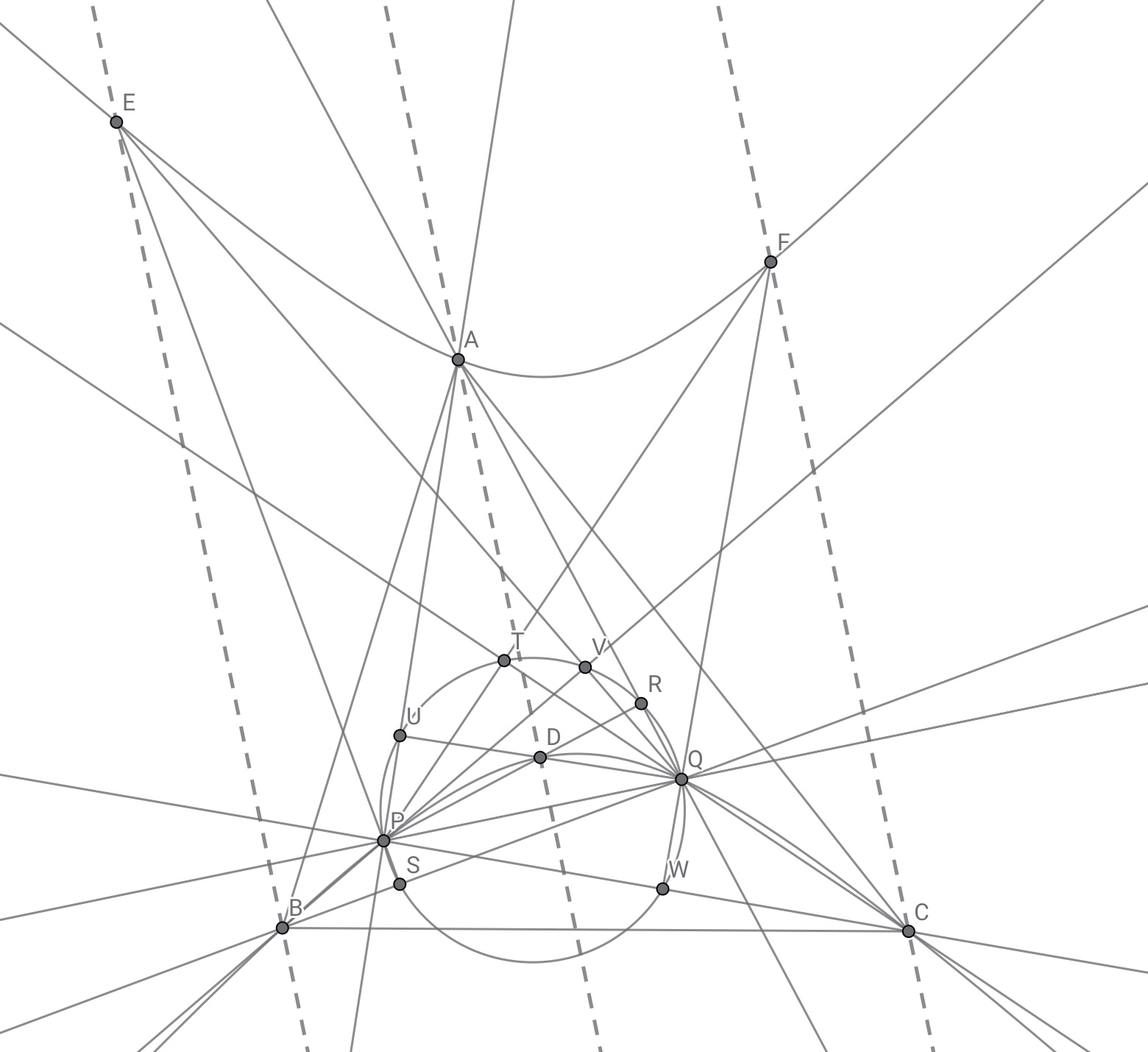垂心と直角双曲線の相性よ
ここで，線分$AD,BE,CF,PQ$の中点を順に点$L,M,N,O$とする．$\varGamma$に対するパスカルの定理から直線$AB$と$DE$の交点，直線$BF$と$CE$の交点，直線$CA$と$DF$の交点は同一直線上にあり，直線$AD,BE,CF$が平行であることからデザルグの定理より直線$AB$と$DE$の交点，直線$BF$と$CE$の交点，直線$AF$と$CD$の交点も同一直線上となる．
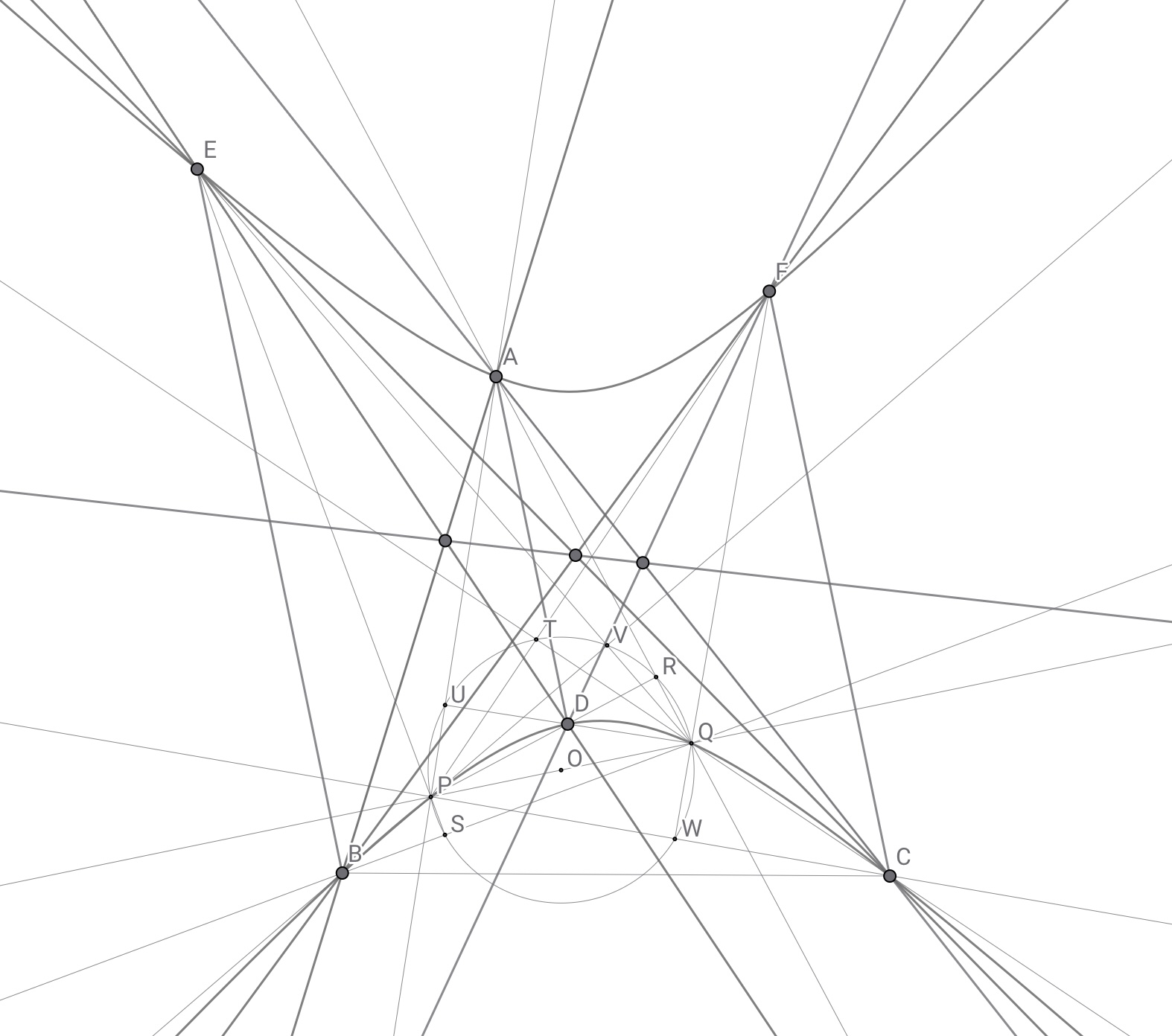パスカルの定理の場合
デザルグの定理の場合
この直線が一致することから，台形$ADCF$に注目すればこの直線が線分$AD$の中点$L$および線分$CF$の中点$N$を通ることは明らかであり，同様の操作を行うことで$3$点$L,M,N$もこの直線上に並ぶことがわかる．
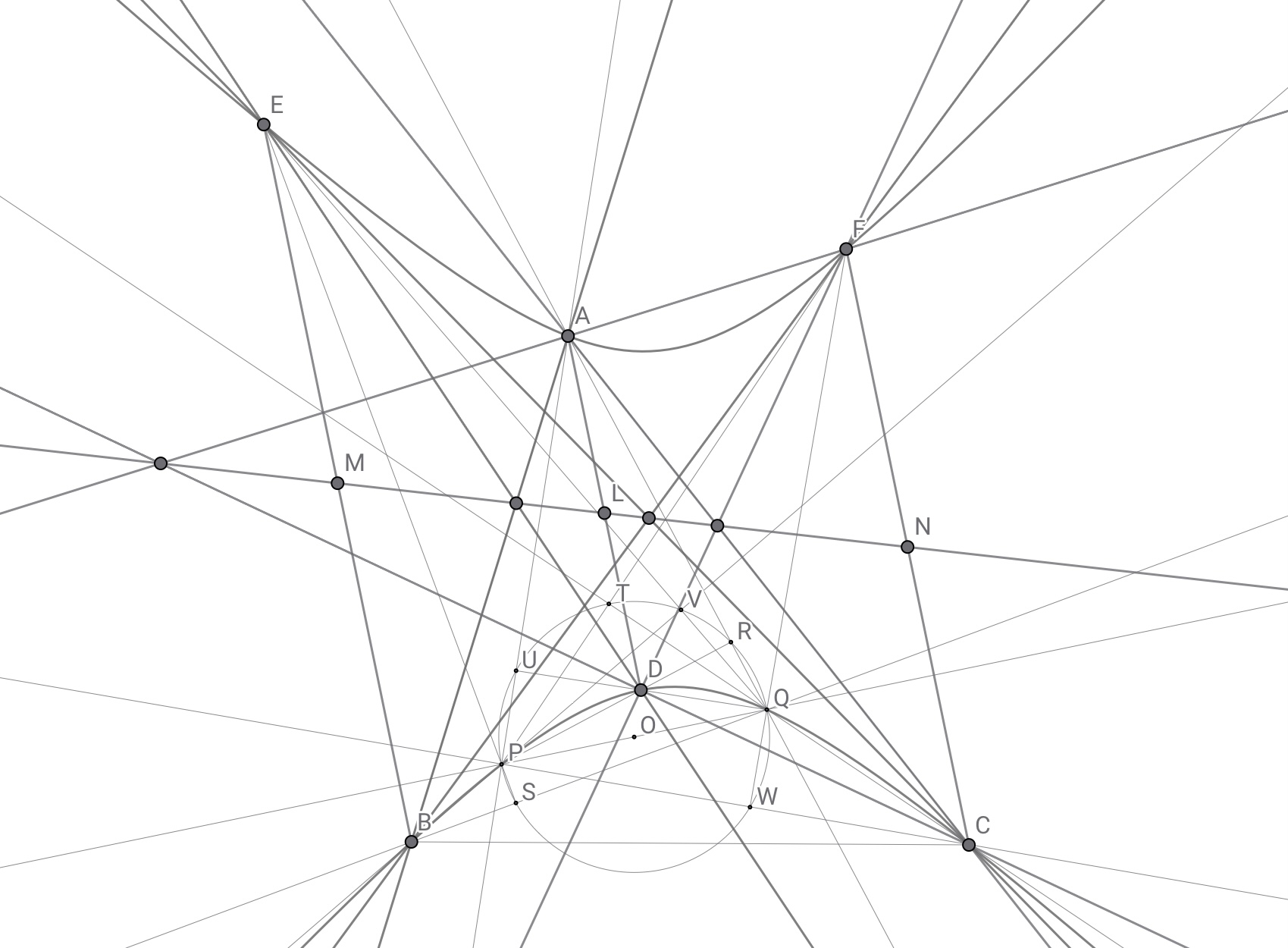円の場合だけ示せば十分という説もある
また，三角形$APQ$の九点円$\omega$を考えると，$4$点$L,O,R,U$は$\omega$上かつ線分$LO$は$\omega$の直径であることから$LR \perp OR$, $LU \perp OU$となる．したがって直線$LR,LU$は円$\varOmega$に接するので，直線$RU$は円$\varOmega$における点$L$の極線である．
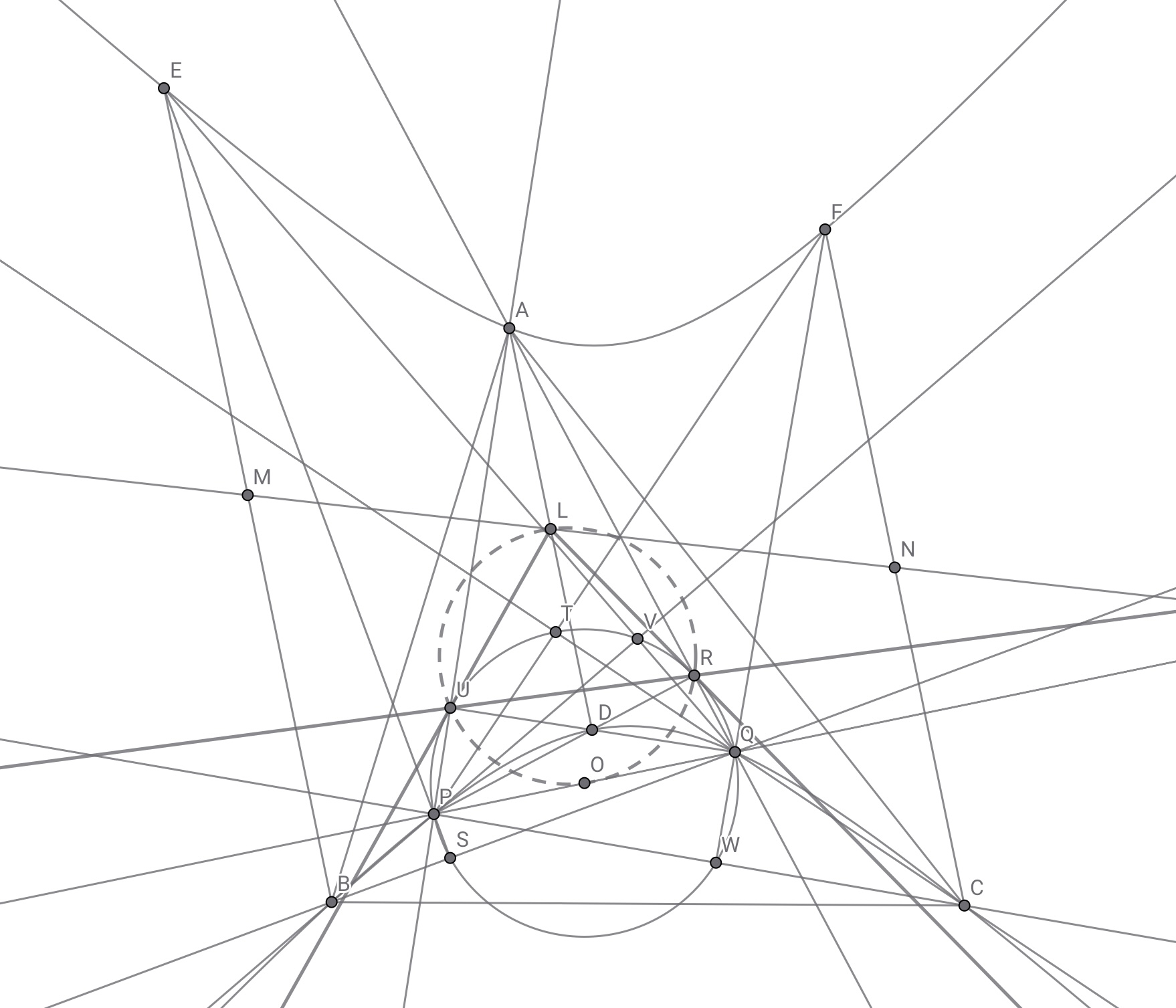極線関連の表現があやふや
同様に直線$SV$は点$M$，直線$TW$は点$N$の極線となる．$3$点$L,M,N$は同一直線上なので，直線$RU,SV,TW$は$1$点（$L,M,N$を通る直線が極線となるような点）で交わる． ◼️
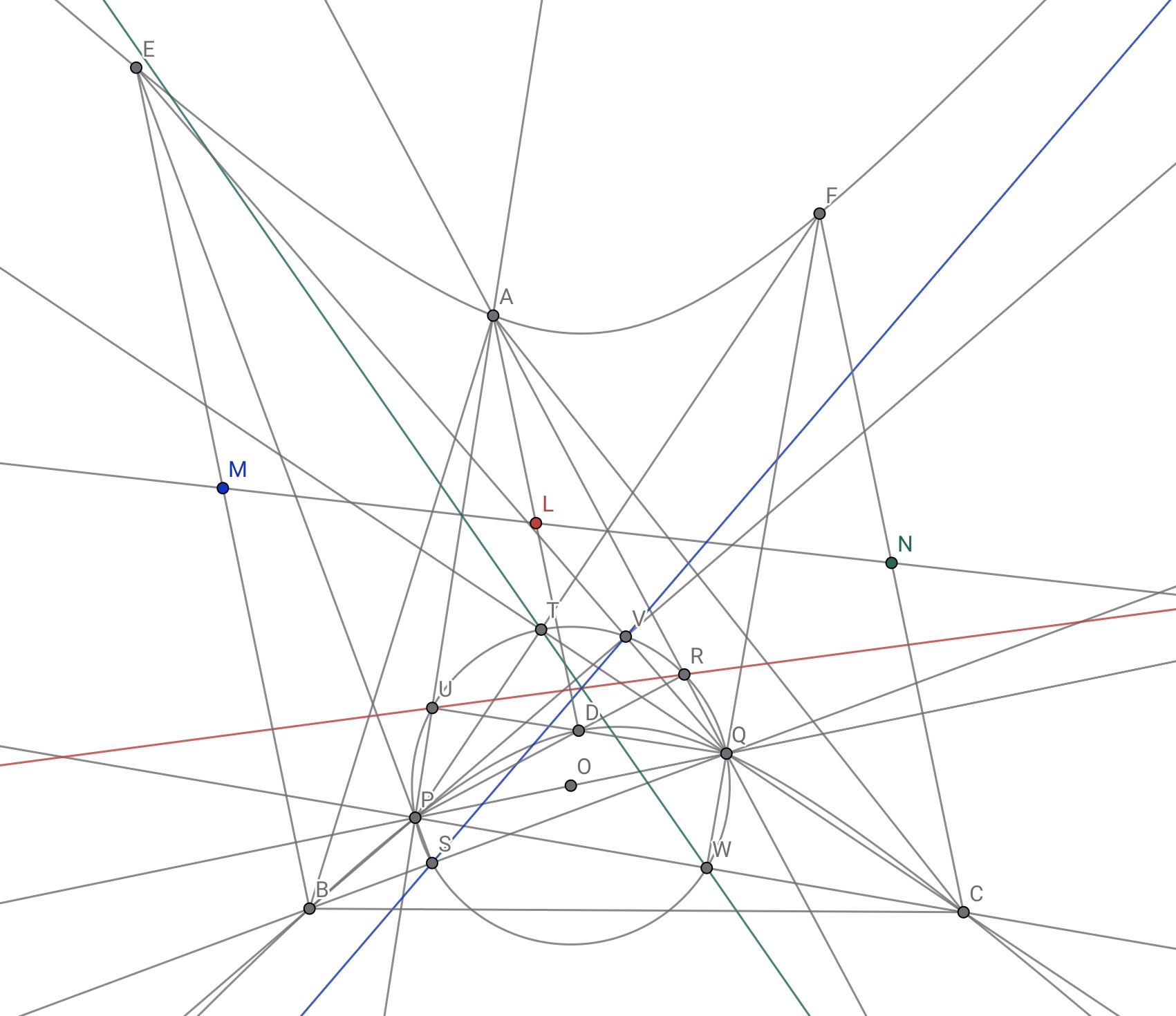極線についての性質も前提とさせてくれ
この補題をもう少し使いやすい形にしておく．
上記の補題の図において$RW \cdot SU \cdot TV=TU \cdot RV \cdot SW$が成り立つ．
円についてのチェバの定理的な感じ
直線$RU,SV,TW$の交点を点$X$とすれば，
$$
\frac{RW}{TU}=\frac{RX}{TX},\frac{SU}{RV}=\frac{SX}{RX},\frac{TV}{SW}=\frac{TX}{SX}
$$
となるので辺々を掛け合わせれば示される． ◼️
上記の補題の図において
直線$AP$と$BQ$のなす角度を$\theta_{AB}$，直線$BP$と直線$AQ$のなす角度を$\theta_{BA}$，
直線$BP$と$CQ$のなす角度を$\theta_{BC}$，直線$CP$と直線$BQ$のなす角度を$\theta_{CB}$，
直線$CP$と$AQ$のなす角度を$\theta_{CA}$，直線$AP$と直線$CQ$のなす角度を$\theta_{AC}$
とすると
$$
\frac{\cos \theta_{AB}\cdot \cos \theta_{BC}\cdot \cos \theta_{CA}}{\cos \theta_{BA}\cdot \cos \theta_{CB}\cdot \cos \theta_{AC}}=1
$$
が成り立つ．
直線$AP$と$BQ$の交点を点$Y$とすれば相似から$\cos\theta_{AB}=\dfrac{YS}{YP}=\dfrac{SU}{PQ}$となる．
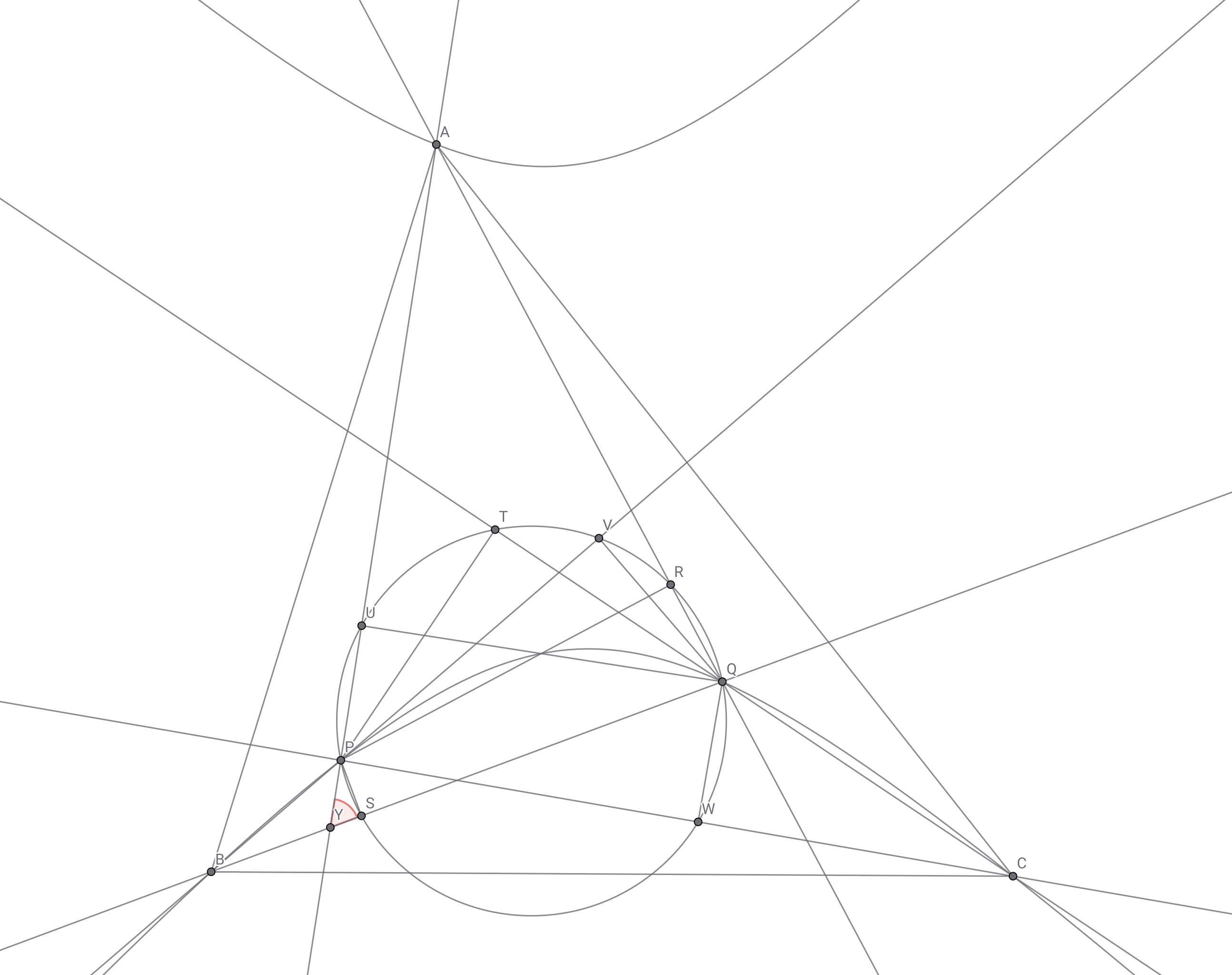図が複雑な時ほどシンプルに考えたい
同様に$\cos\theta_{BA}=\dfrac{VR}{PQ}$，$\cos\theta_{BC}=\dfrac{TV}{PQ}$，$\cos\theta_{CB}=\dfrac{SW}{PQ}$，$\cos\theta_{CA}=\dfrac{RW}{PQ}$，$\cos\theta_{AC}=\dfrac{TU}{PQ}$となるので補題$2$から所望の式が得られる． ◼️
補題$3$を用いて今回の主題である問題を解いていこう．すでに冒頭で問題を確認いただいていると思うが，改めて問題を以下に記載する．
どの$2$辺の長さも等しくない鋭角三角形$ABC$がある．また，$0<\theta <\pi$なる実数$\theta$および点$D,E,F,G,H,I,J,K,L,M,N,O$があり，以下の条件をすべてみたしている．
- 点$D,E,F,G$は直線$BC$に関して$A$と反対側にあり，四角形$BCDE,CBFG$はそれぞれ$\angle BCD=\theta ,\angle CBF=\theta$をみたすひし形である．
- 点$H,I,J,K$は直線$CA$に関して$B$と反対側にあり，四角形$CAHI,ACJK$はそれぞれ$\angle CAH=\theta ,\angle ACJ=\theta$をみたすひし形である．
- 点$L,M,N,O$は直線$AB$に関して$C$と反対側にあり，四角形$ABLM,BANO$はそれぞれ$\angle ABL=\theta ,\angle BAN=\theta$をみたすひし形である．
直線$BJ,CL$の交点を$P$，直線$BK,CM$の交点を$Q$，直線$CN,AD$の交点を$R$，直線$CO,AE$の交点を$S$，直線$AF,BH$の交点を$T$，直線$AG,BI$の交点を$U$とする．このとき，三角形$APQ$の外接円，三角形$BRS$の外接円，三角形$CTU$の外接円すべてが共通する$2$点を通ることを示せ．
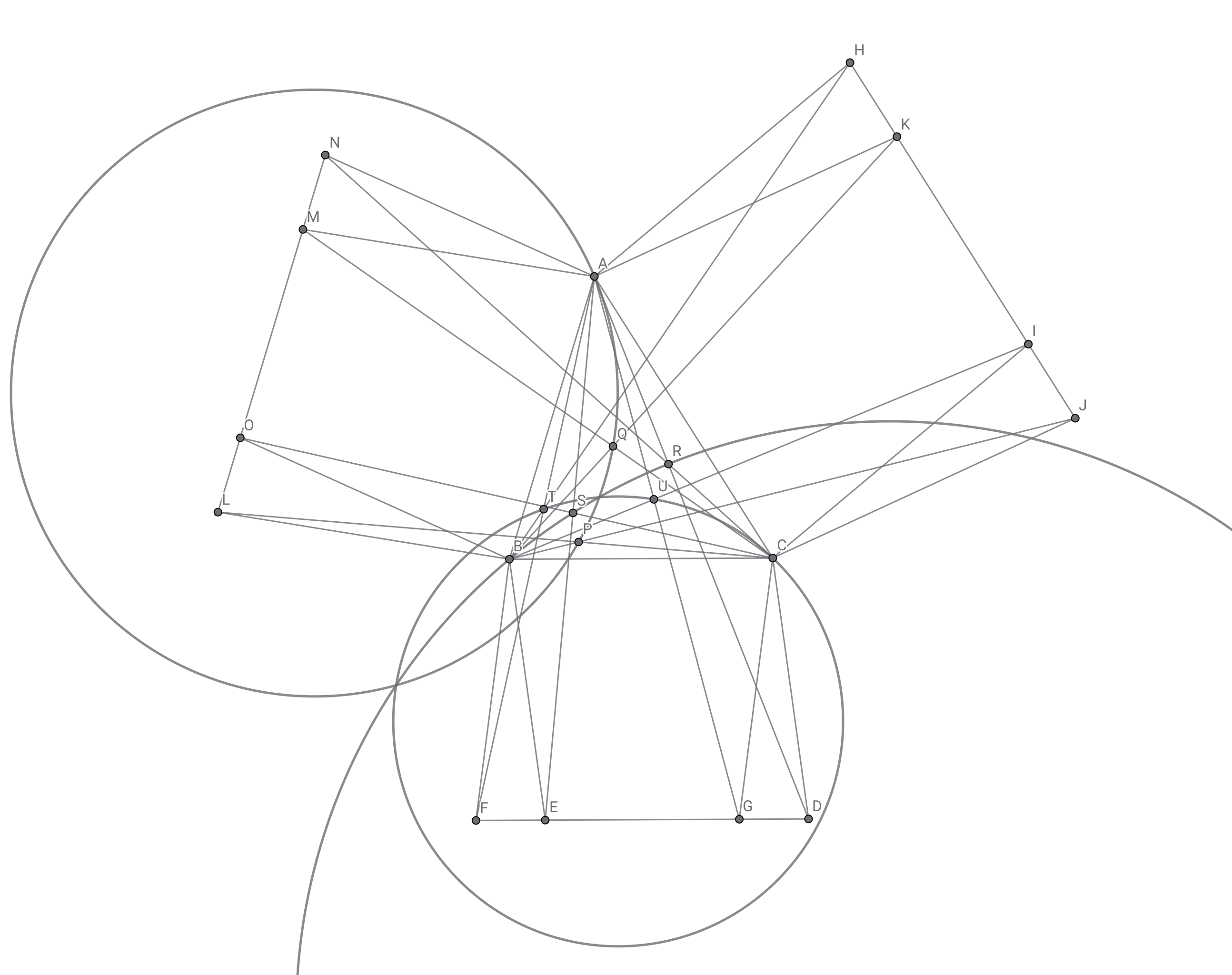共軸問題は比較的新しめの典型な気がする
一つ一つの要素は見たことのある構図ではあるが，組み合わさって外接円をトッピングするとだいぶ凶悪に仕上がってしまっている．この問題と先の補題がどう関わるのかをまずは明かしていくために幾つかの命題を示していく．
直線$AP,BF,CD$は一点で交わる．
直線$BF$と$CD$の交点を$A_1$とする．また三角形$ABC$の面積を$[ABC]$で表すとする．
$\angle BAL=\angle CAJ$および$AL:AJ=AB:AC$より$[ACL]=[ABJ]$
$\theta$の回転を考慮すると直線$AF$と$BC$のなす角度は$\angle DCL$と等しくなるため，$[ABFC]=[CDL]$となり，同様の考察から$[ACDB]=[BFJ]$も分かり$[CDL]=[BFJ]$が導かれる．
したがって$BA_1=CA_1$と合わせて$\dfrac{[ABP]}{[ACP]}=\dfrac{[FBP]}{[DCP]}=\dfrac{[A_1BP]}{[A_1CP]}$より$3$点$A_1,A,P$は同一直線上． ◼️
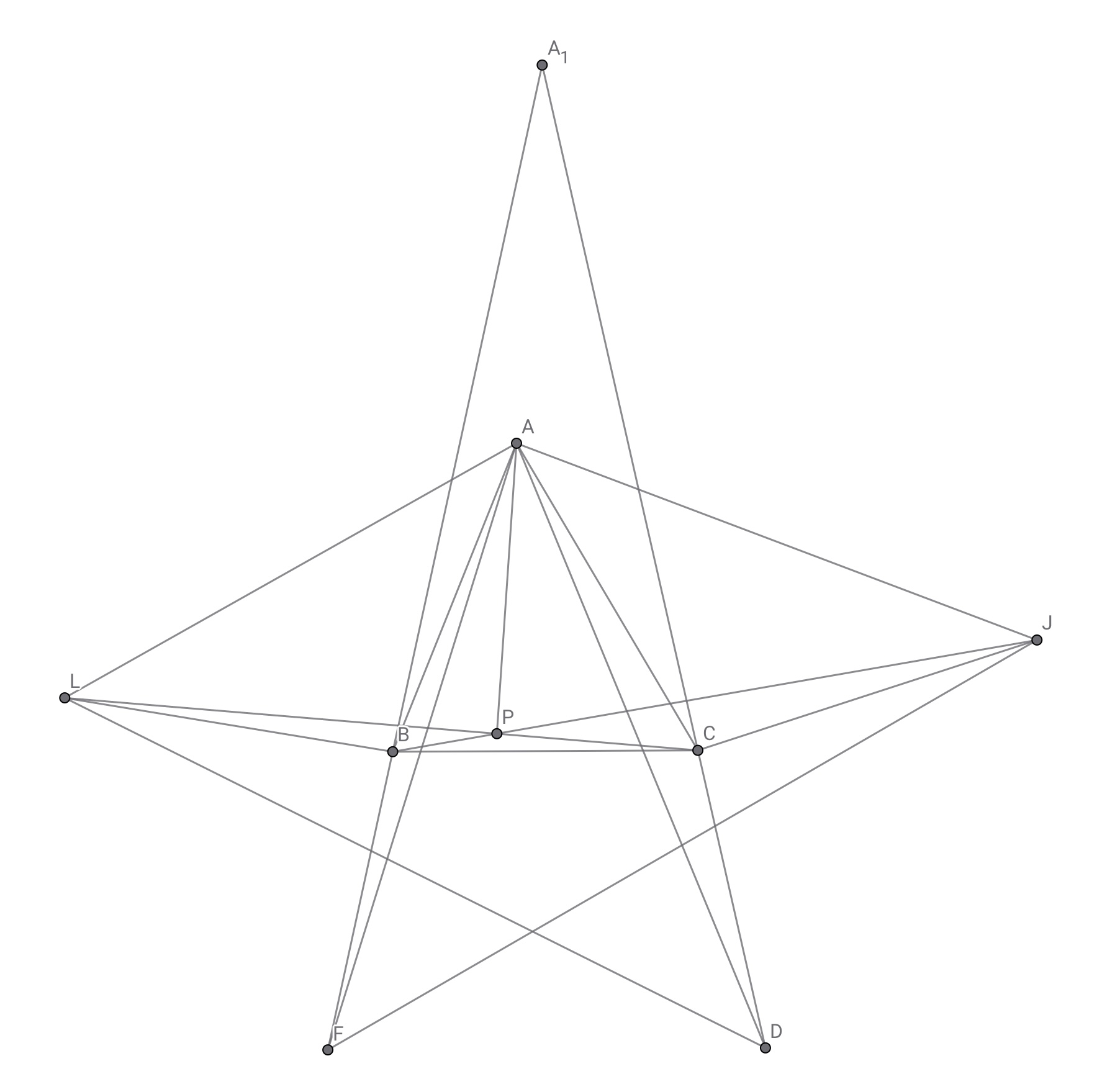これだけでも何らかの問題で出されてそう
直線$BH$と$CN$の交点を$X$，直線$CL$と$AF$の交点を$Y$，直線$AD$と$BJ$の交点を$Z$とする．
円$BCGE$の中心を$O_A$とすると点$A,O_A$はいずれも$\angle BXC$の内角二等分線上にある．
$4$点$A,N,B,X$と$A,H,C,X$はそれぞれ同一円周上にあり
$\angle AXN=\angle ABN=\angle ACH=\angle AXH$
$\angle O_ABC=\angle ABN=\angle AXN$より$\angle O_ABC+\angle O_ACB=\angle BXC$から$B,X,C,O_A$は同一円周上となるので$\angle BXO_A=\angle CXO_A$ ◼️
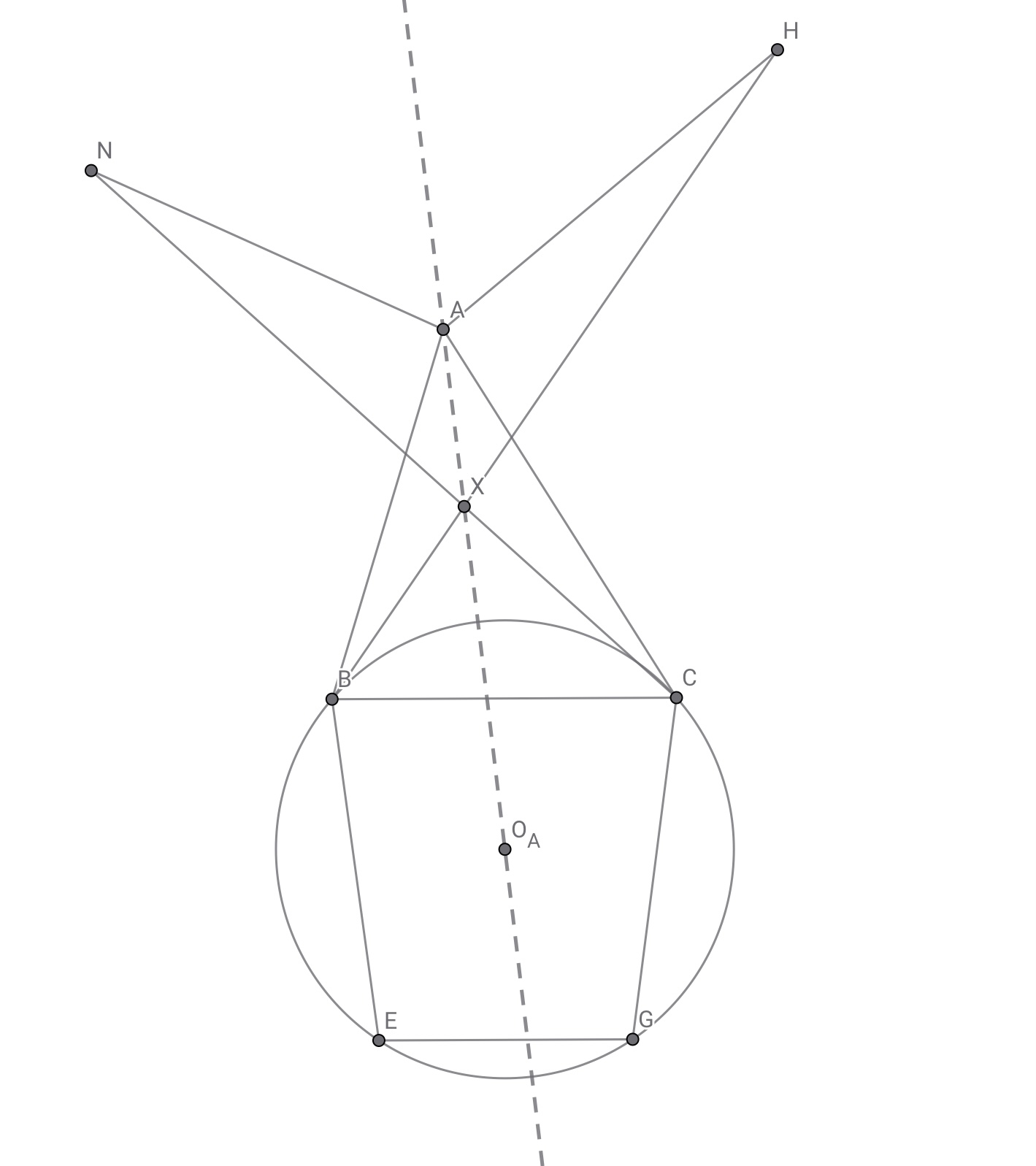このくらいのやさしさなら安心です
補題の活用に向けた下ごしらえが整ったので，この問題に適用していこう．直線$JC$と$HA$の交点を$B_1$，直線$NA$と$LB$の交点を$C_1$，円$CAKI$の中心を$O_B$，円$ABOM$の中心を$O_C$とする．
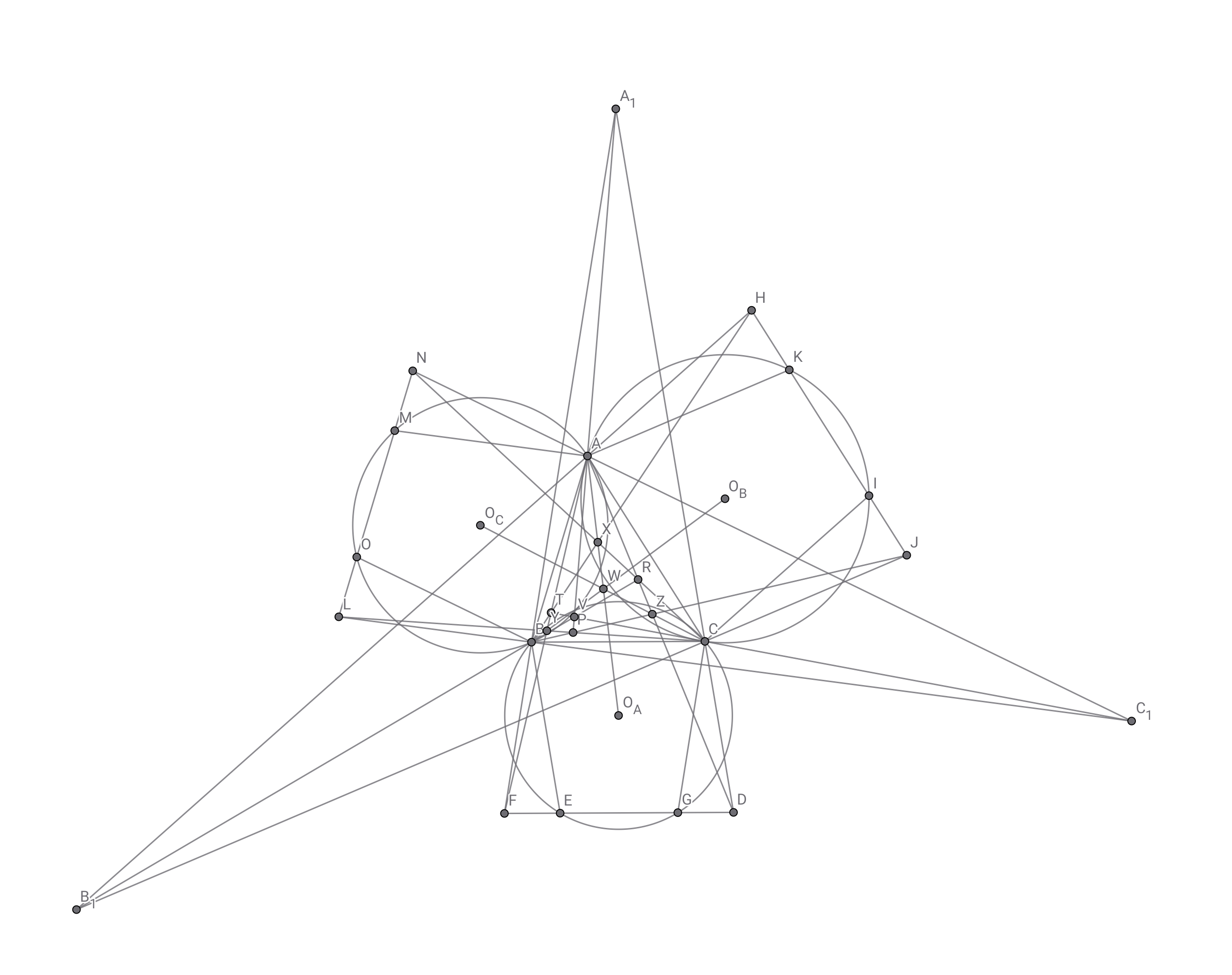内側に多く外にも広がる図、ゴチャりがち
キーペルト点の条件を満たすことから直線$AA_1,BB_1,CC_1$は一点で交わり，直線$AO_A,BO_B,CO_C$も一点で交わる．これらの点を順に$V,W$とすれば$A,B,C,V,W$はキーペルト双曲線上にある．
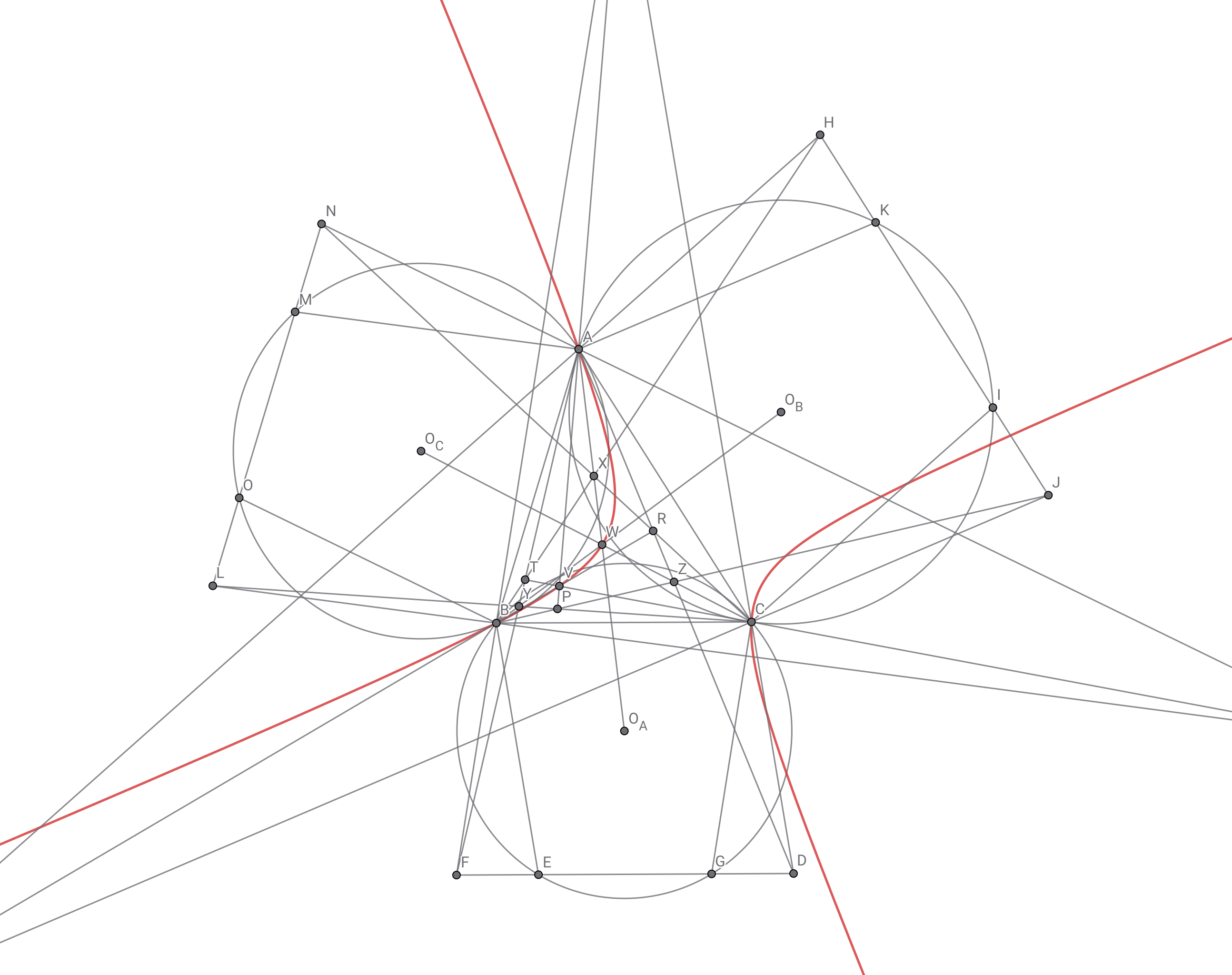赤線がキーペルト双曲線である
キーペルト双曲線は直角双曲線なので補題$3$が適用できる．ここで
直線$AV$と$BW$のなす角度を$\theta_{AB}$，直線$BV$と直線$AW$のなす角度を$\theta_{BA}$，
直線$BV$と$CW$のなす角度を$\theta_{BC}$，直線$CV$と直線$BW$のなす角度を$\theta_{CB}$，
直線$CV$と$AW$のなす角度を$\theta_{CA}$，直線$AV$と直線$CW$のなす角度を$\theta_{AC}$
と定義しておく．ここまでに示した命題から直線$AV,BV,CV,AW,BW,CW$は直線$AP,BR,CT,AX,BY,CZ$と同一である．元の問題に違和感なく適用できたので本題の証明に進んでいこう．
三角形$APQ$の外接円と三角形$BRS$の外接円の交点の一つを$T_1$とする．頂点名が被っているのは問題にも責任があると思う．なお交点を持つこと自体の証明は$AB< AC$であれば点$B,S$が円$APQ$の内部にあり点$S$は外部にあることから示される．
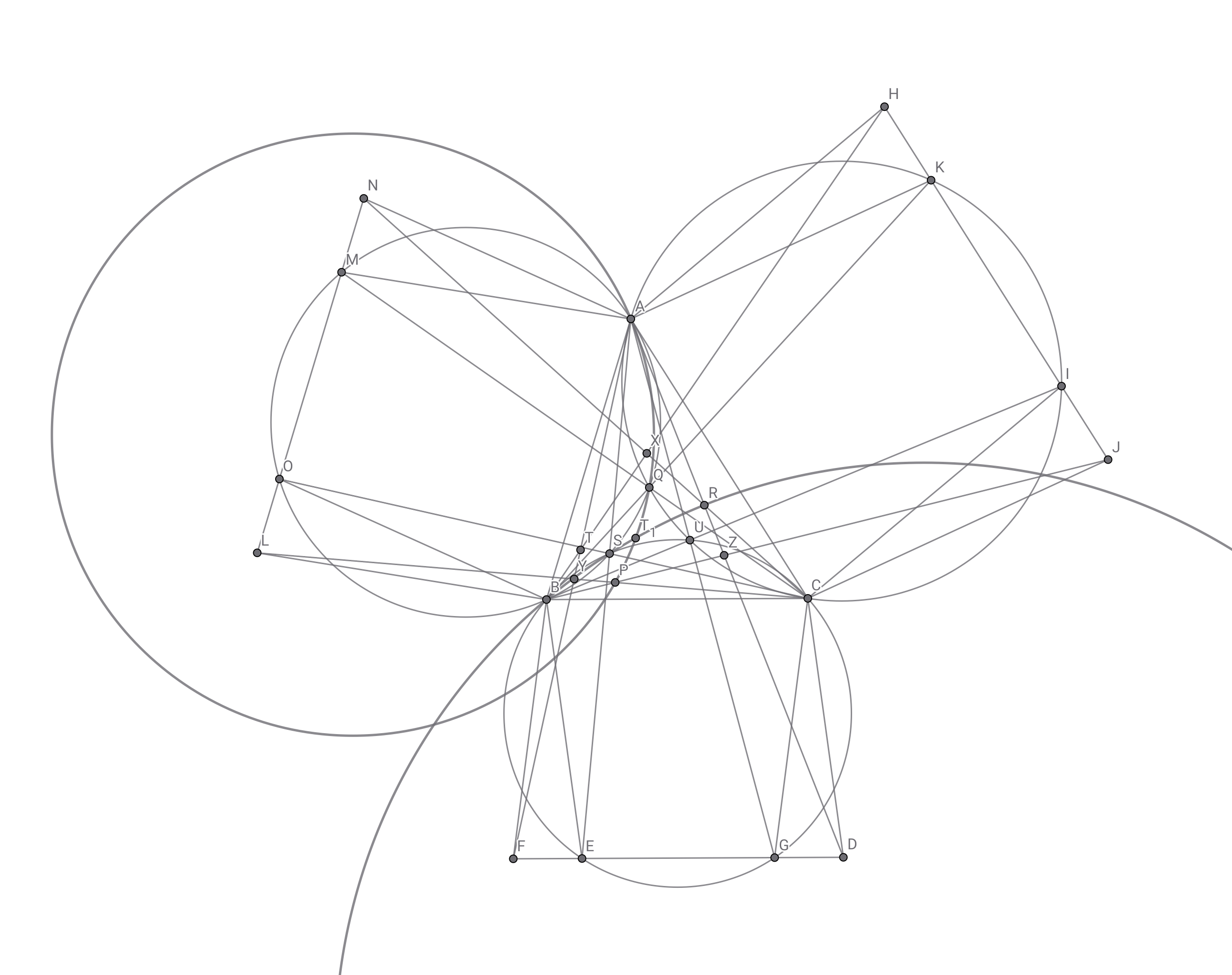ようやく考えるべき外接円の一部が顕現
円$BEGCUS,CIKAQU,AMOBSQ$を順に円$\varOmega_A,\varOmega_B,\varOmega_C$とすると共軸に関する性質より
$\dfrac{Pow\varOmega_B(T_1)}{Pow\varOmega_C(T_1)}=\dfrac{Pow\varOmega_B(P)}{Pow\varOmega_C(P)}$，$\dfrac{Pow\varOmega_C(T_1)}{Pow\varOmega_A(T_1)}=\dfrac{Pow\varOmega_C(R)}{Pow\varOmega_A(R)}$
となる．方べきについて考えたくなってくるはずである．
直線$XB,XC$が円$\varOmega_A$と再び交わる点を順に$B_X,C_X$，直線$YC,YA$が円$\varOmega_B$と再び交わる点を順に$C_Y,A_Y$，直線$ZA,ZB$が円$\varOmega_C$と再び交わる点を順に$A_Z,B_Z$ととする．
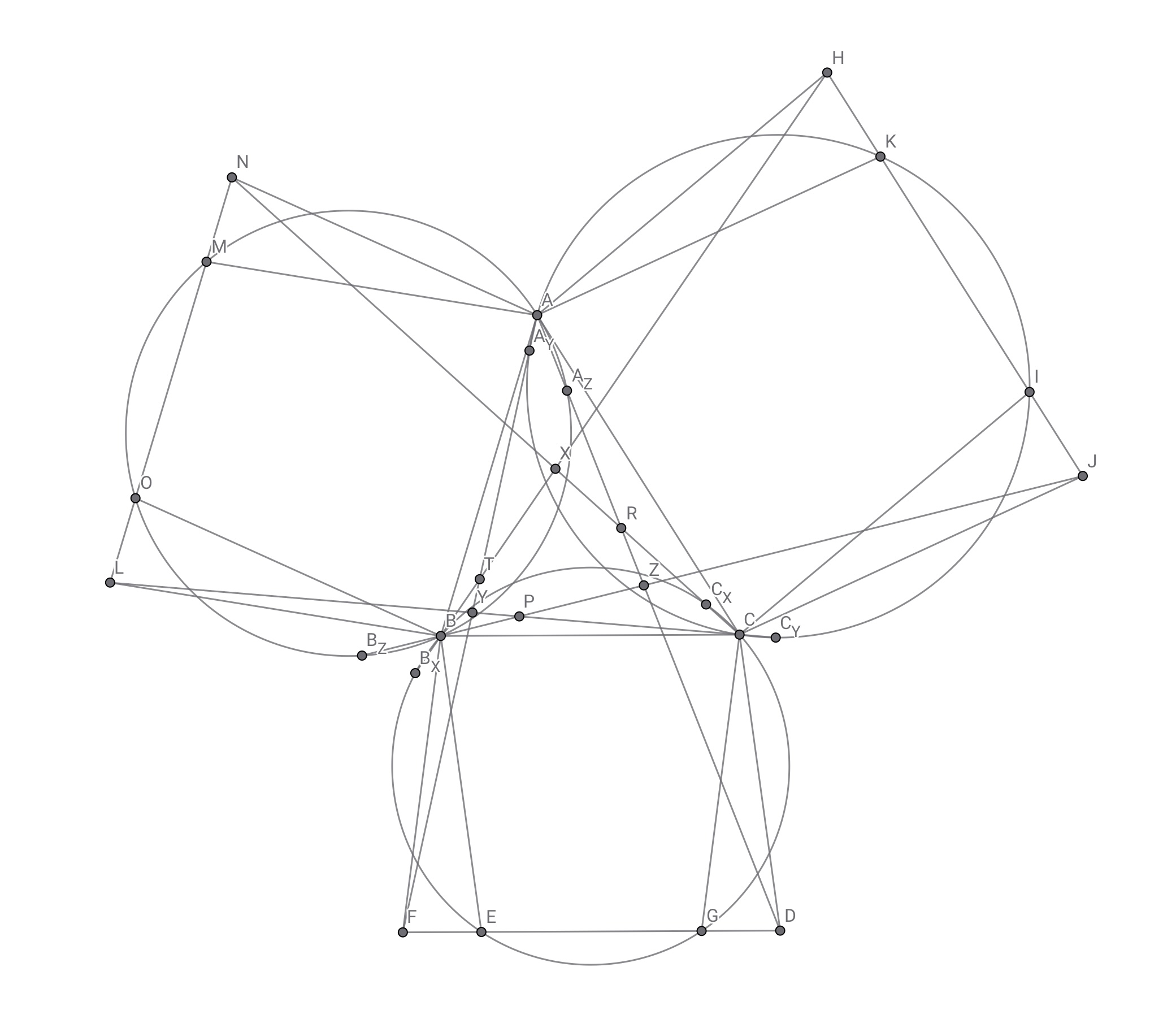新しくつけた点の意味付けを考える時間
円$\varOmega_A$は$\angle BXC$の内角二等分線に関して対称なので$XB_X=XC,XC_C=XB$となる．したがって$Pow\varOmega_A(T)=TB \cdot TB_X=TB\cdot (XC-XT)=TB\dfrac{TC\cos\theta_{CA}}{\cos (\angle BXC/2)}$
$Pow\varOmega_A(R)=RC \cdot RC_X=RC\cdot (XB-XR)=RC\dfrac{RB\cos\theta_{BA}}{\cos (\angle BXC/2)}$
が言える．
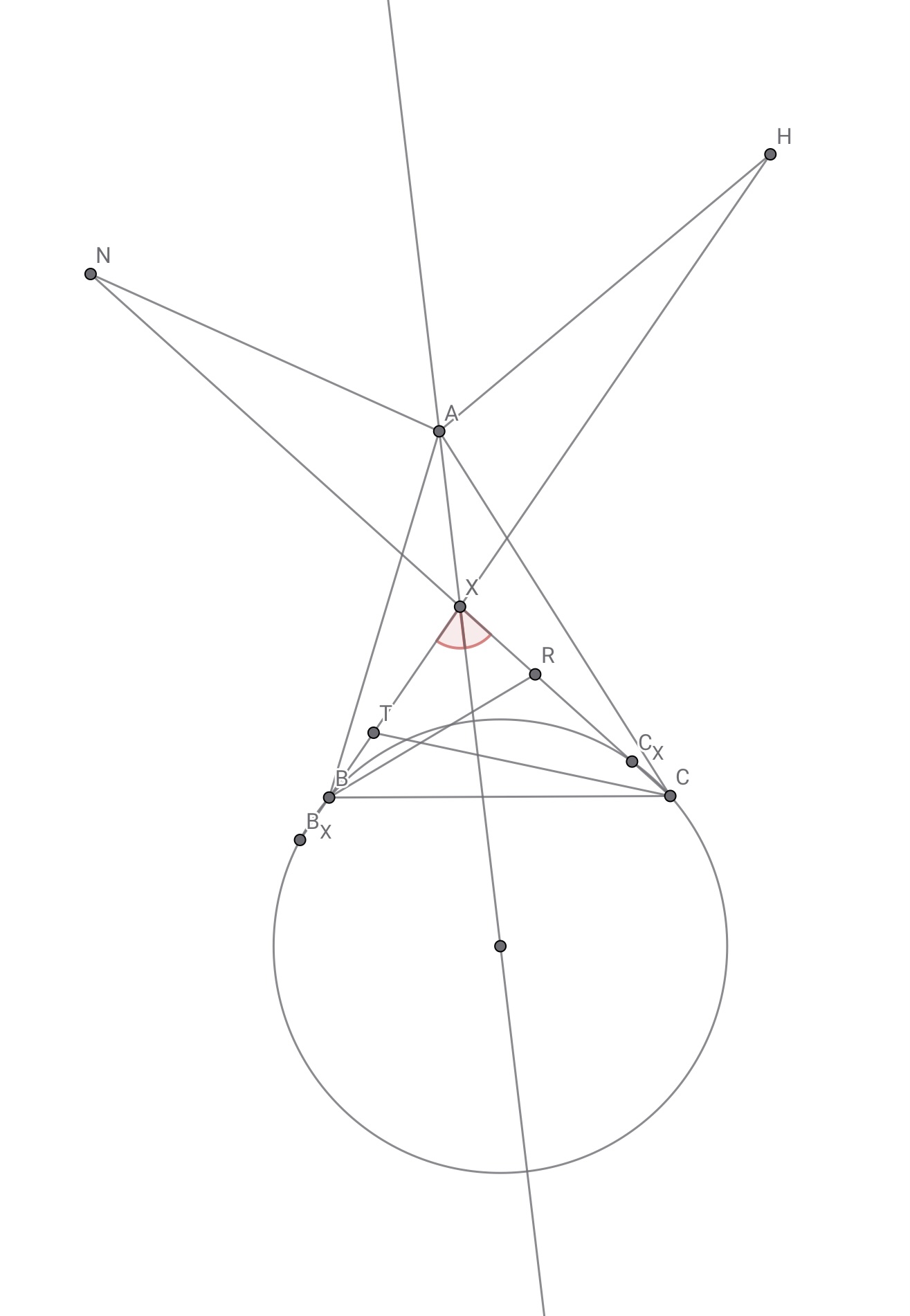あのときのcosをここで
よって
$\dfrac{Pow\varOmega_A(T)}{Pow\varOmega_A(R)}\cdot\dfrac{Pow\varOmega_B(P)}{Pow\varOmega_B(T)}\cdot\dfrac{Pow\varOmega_C(R)}{Pow\varOmega_C(P)}=\dfrac{TB\cdot TC\cos\theta_{CA}}{RC\cdot RB\cos\theta_{BA}}\cdot\dfrac{PC\cdot PA\cos\theta_{AB}}{TA\cdot TC\cos\theta_{CB}}\cdot\dfrac{RA\cdot RB\cos\theta_{BC}}{PB\cdot PA\cos\theta_{AC}}$
$=\dfrac{PC}{PB}\cdot\dfrac{RA}{RC}\cdot\dfrac{TB}{TA}=\dfrac{\sin\angle PBC}{\sin\angle PCB}\cdot\dfrac{\sin\angle RCA}{\sin\angle RAC}\cdot\dfrac{\sin\angle TAB}{\sin\angle TBA}=\dfrac{CJ}{CB}\cdot\dfrac{AN}{AC}\cdot\dfrac{BF}{BA}=1$
となるので
$\dfrac{Pow\varOmega_B(T_1)}{Pow\varOmega_A(T_1)}=\dfrac{Pow\varOmega_B(T_1)}{Pow\varOmega_C(T_1)}\cdot\dfrac{Pow\varOmega_C(T_1)}{Pow\varOmega_A(T_1)}=\dfrac{Pow\varOmega_B(P)}{Pow\varOmega_C(P)}\cdot\dfrac{Pow\varOmega_C(R)}{Pow\varOmega_A(R)}=\dfrac{Pow\varOmega_B(T)}{Pow\varOmega_A(T)}$
が言える．円$\varOmega_A$と円$\varOmega_B$の交点が点$C,U$であることから，$4$点$C,U,T,T_1$は同一円周上にあることがわかる．点$T_1$ではない方の交点についても同様の議論ができるため，三角形$APQ$の外接円，三角形$BRS$の外接円，三角形$CTU$の外接円は共通の$2$点を取ることが示された． ◼️
かなり冗長となってしまったが議論の抜けはないだろうか．補題$3$と最後の段落の議論がしたかっただけなので他の部分はさらっと流していただきたい．気づいたことがあれば追記するかも．
