国際信州学院大学観光学部R6第二問を、高校数学+α＋βくらいで解く

ある定数$c$で積分区間を分けて、別々で収束を証明する。
$\displaystyle A_1 = \int_0^c e^{-t}t^{x-1}\: dt$
$\displaystyle A_2 = \int_c^\infty e^{-t}t^{x-1}\: dt$
まず、被積分関数が$t>0$で常に0以上なので、
$0\leq A_1$、$0\leq A_2$

$A_1$について、
また、$e^0 =1$で$e^{-t}$は単調減少なので$e^{-t}\leq 1$から、
$$A_1 \leq \int_0^c t^{x-1}\: dt$$
$x>0$の仮定から、
\begin{eqnarray} \int_0^c t^{x-1}\: dt &=& \left[\dfrac{t^x}{x}\right]_0^c\\ &=& \dfrac{c^x}{x}<\infty \end{eqnarray}
$A_2$について、

1以上の任意の自然数$n$をとして、関数$\displaystyle f(x) = x-\log\left(1+x+\dfrac{x^2}{2}+\cdots + \dfrac{x^n}{n!}\right)$ $(x>0)$とすると、$\displaystyle \lim_{x\rightarrow +0}f(x)=0$かつ、
$$f'(x) = 1-\dfrac{1+x+\frac{x^2}{2}+\cdots + \frac{x^{n-1}}{(n-1)!}}{1+x+\frac{x^2}{2}+\cdots + \frac{x^n}{n!}}>0$$
よって$x>0$で$f(x)>0$が成り立ち、整理して指数を取ると、
$$e^x > 1+x+\dfrac{x^2}{2} + \cdots + \dfrac{x^n}{n!}$$
つまり$e^{-x}<\dfrac{n!}{x^n}$
よって、$n>x$なる$n$を取ってきて、
\begin{eqnarray} A_2 &\leq& \int_c^\infty \dfrac{n!}{t^{n+1-x}}\: dt\\ &=& \left[\dfrac{n!}{(x-n)t^{n-x}}\right]_{c}^\infty\\ &=& \dfrac{n!}{(n-x)c^{n-x}} <\infty \end{eqnarray}
よって、$\Gamma(x)$は$x>0$で収束する。

\begin{eqnarray} \Gamma(x+1) &=& \int_0^\infty e^{-t}t^{x}\: dt\\ &=& \left[-e^{-t}t^x\right]_0^\infty + x\int_0^\infty e^{-t}t^{x-1}\: dt\\ &=& x\Gamma(x) \end{eqnarray}
2段目の極限は、定理1の議論と同様にして導ける。

$1+x+\dfrac{x^2}{2}\leq e^x$の証明は定理1の証明の途中で示している。
もう一つの不等式について、
$f(x) = 1+x+x^2-e^x$とすると、$f'(x)=1+2x-e^x, f''(x)=2-e^x$となり、
$f''(x)\geq 0\: (0\leq x \leq \log2)$,$f'(0) = 0$であるので、$f'(x)\geq 0\: (0\leq x \leq \log 2)$
また、$f(0)=0$であるので、
$f(x)\geq 0\: (0\leq x\leq \log 2)$
よって$e^x \leq 1+x+x^2\: (0\leq x\leq \log 2)$

まずは、$\displaystyle\int_0^\infty e^{-t}t^{x-1}(\log t)^n\: dt$が収束することを示そう。
$0\leq t\leq 1$で$e^{-t}\leq 1$である。$1\leq t$で$(\log t)^n\leq t^n$であることは、$f(t) = t-\log t$の増減表を書くことで示せる。
よって、
\begin{eqnarray} \int_{0}^\infty e^{-t}t^{x-1}(\log t)^n\: dt &\leq& \int_0^1 t^{x-1}(\log t)^n\: dt + \int_1^\infty e^{-t}t^{n+x-1}\: dt\\ &<&\infty\quad \left(\lim_{x\rightarrow+ 0}x^{a}(\log x)^n = 0\quad (a>0)\text{であることは、}\lim_{x\rightarrow +\infty}\dfrac{\log x}{x^{\frac{a}{n}}}=0\text{より従う。　また、この極限は$e^x > \dfrac{x^n}{n!}$より従う。また、2項目は$\Gamma(n+x)$より小さい。}\right) \end{eqnarray}
\begin{eqnarray} \Gamma(x+h) &=& \int_0^\infty e^{-t}e^{(x+h-1)\log t}\: dt\\ &=& \int_0^\infty e^{-t}e^{(x-1)\log t}e^{h\log t}\: dt \end{eqnarray}
$0\leq h\log t\leq \log 2$を満たす、つまり十分小さい$h$において、
$$\int_0^\infty e^{-t}e^{(x-1)\log t}\left(1+h\log t+\dfrac{h^2(\log t)^2}{2}\right)\: dt \leq \Gamma(x+h) \leq \int_0^\infty e^{-t}e^{(x-1)\log t}\left(1+h\log t+h^2(\log t)^2\right)\: dt$$
$$\int_0^\infty e^{-t}e^{(x-1)\log t}\left(h\log t+\dfrac{h^2(\log t)^2}{2}\right)\: dt \leq \Gamma(x+h)-\Gamma(x) \leq \int_0^\infty e^{-t}e^{(x-1)\log t}\left(h\log t+h^2(\log t)^2\right)\: dt$$
$$\lim_{h\rightarrow 0}\dfrac{1}{h}\int_0^\infty e^{-t}e^{(x-1)\log t}\left(h\log t+\dfrac{h^2(\log t)^2}{2}\right)\: dt \leq \lim_{h\rightarrow 0}\dfrac{1}{h}\left(\Gamma(x+h)-\Gamma(x) \right)\leq \lim_{h\rightarrow 0}\dfrac{1}{h}\int_0^\infty e^{-t}e^{(x-1)\log t}\left(h\log t+h^2(\log t)^2\right)\: dt$$
左側も右側も、同じ収束値であるので、挟み撃ちの原理から、
$$\Gamma '(x) = \lim_{h\rightarrow 0}\dfrac{\Gamma(x+h)-\Gamma(x)}{h}=\int_{0}^\infty e^{-t}t^{x-1}\log t\: dt$$
この議論は、$\Gamma '(x)$、$\Gamma ''(x)\cdots \Gamma^{(n-1)}(x)$に対しても同様に行えるので、式を得る。

\begin{eqnarray*}   \{\log \Gamma (x)\}'' = \left(\dfrac{\Gamma '(x)}{\Gamma (x)}\right)' &=& \dfrac{\Gamma ''(x)\Gamma(x)-\Gamma '(x)^2}{\Gamma (x)^2}\\   &=& \dfrac{1}{\Gamma (x)}\left(\Gamma''(x) - \left(\dfrac{\Gamma (x)'}{\Gamma(x)}\right)^2\Gamma(x)\right)\\   &=& \dfrac{1}{\Gamma (x)}\left(\Gamma''(x)-2\dfrac{\Gamma '(x)}{\Gamma(x)}\Gamma '(x) + \left(\dfrac{\Gamma (x)'}{\Gamma(x)}\right)^2\Gamma(x)\right)\\   &=& \dfrac{1}{\Gamma (x)}\int_{0}^{\infty}e^{-t}t^{x-1}\left\{(\log t)^2 -2\dfrac{\Gamma '(x)}{\Gamma(x)} + \left(\dfrac{\Gamma '(x)}{\Gamma(x)}\right)^2\right\}\: dt\\   &=& \dfrac{1}{\Gamma (x)}\int_{0}^{\infty}e^{-t}t^{x-1}\left(\log t - \dfrac{\Gamma '(x)}{\Gamma(x)}\right)^2\: dt \geq 0 \end{eqnarray*}

$0< x\leqq 1$、$n$は$0$以上の整数だとすると、
$$f(x+n) = (x+n-1)(x+n-2)\cdots (x+1)xf(x)$$
となるので、いかなる正の実数に対しても、$0< x\leqq 1$の定義域に帰着する。
ここで、$\log f(x)$は下に凸なので、$0< x\leqq 1$を満たす実数、$n$を2以上の自然数とすると以下の不等式が成立する。
$$\dfrac{\log f(-1+n) - \log f(n)}{(-1+n)-n}\leqq \dfrac{\log f(x+n) - \log f(n)}{(x+n)-n}\leqq \dfrac{\log f(1+n) - \log f(n)}{(1+n)-n}$$
$f(n+1) = n!$、$f(n) = (n-1)!$、$f(n-1) = (n-2)!$であるから上式は
\begin{eqnarray*} \log (n-1) \leqq &\dfrac{\log f(x+n) - \log(n-1)!}{x}& \leqq \log n\\ x\log (n-1) \leqq &\log f(x+n) - \log (n-1)! &\leqq x\log n\\ x\log (n-1) + \log (n-1)! \leqq &\log f(x+n)& \leqq x\log n + \log (n-1)!\\ \log \left\{(n-1)^x (n-1)!\right\} \leqq &\log f(x+n)&\leqq \log \left\{n^x (n-1)!\right\} \end{eqnarray*}
$\log$は単調増加なのでそのまま外せて
$$(n-1)^x (n-1)! \leqq f(x+n) \leqq n^x (n-1)!$$
ここで、$f(x+n)$を先ほどの方法で変形させて整理すると、
$$\dfrac{(n-1)^x (n-1)!}{x(x+1)\cdots (x+n-1)}\leqq f(x)\leqq \dfrac{n^x (n-1)!}{x(x+1)\cdots (x+n-1)} = \dfrac{n^x n!}{x(x+1)\cdots (x+n)}\dfrac{x+n}{n}$$
この式は2以上の任意の自然数$x$に対して成立するものであるから、左辺に対して$n$を$n+1$にしたものも当然成立して
$$\dfrac{n^x n!}{x(x+1)\cdots (x+n)}\leqq f(x)\leqq \dfrac{n^x n!}{x(x+1)\cdots (x+n)}\dfrac{x+n}{n}$$
$$f(x)\leqq \dfrac{n^x n!}{x(x+1)\cdots (x+n)}\leqq f(x)\dfrac{x+n}{n}$$
$n\rightarrow \infty$で下限と上限は同じ$f(x)$に収束するので、挟み撃ちの原理から、
$$f(x) = \lim_{n\rightarrow \infty}\dfrac{n^x n!}{x(x+1)\cdots (x+n)}\quad \text{(これをガウスの無限乗積表示といいます。)}$$
という一義的な関数に定まる。また、$\Gamma(x)$はこの条件を全て満たすことからこの極限が収束することも分かり、$f(x) = \Gamma(x)$であることも言える。

$x=\sin ^2 \theta$に変数変換する。$x:0\rightarrow 1$で$\theta :0\rightarrow \frac{\pi}{2}$、$\dfrac{dx}{d\theta} = 2\sin\theta\cos\theta$であるので、
\begin{eqnarray} B(a,b) &=& \int_{0}^{\frac{\pi}{2}}(\sin ^2 \theta)^{a-1}(\cos ^2\theta)^{a-1}\cdot 2\sin \theta\cos\theta\: d\theta\\   &=& 2\int_{0}^{\frac{\pi}{2}}\sin ^{2a-1}\theta \cos ^{2b-1}\theta d\theta \end{eqnarray}

\begin{eqnarray} \Gamma(a)\Gamma(b) &=& \int_0^\infty x^{a-1}e^{-x}\: dx \int_0^\infty y^{b-1}e^{-y}\: dy\\ &=& \int_0^\infty\left(\int_0^\infty x^{a-1}y^{b-1}e^{-(x+y)}\: dy\right)\: dx \end{eqnarray}
ここで、$y$に対して$y=t-x$という変数変換を行うと、$y:0\to\infty$で$t:x\to \infty$となるので、
$$\int_0^\infty \left(\int_x^\infty x^{a-1}(t-x)^{b-1}e^{-t}\: dt\right)\: dx$$
と表せる。今、積分範囲は下図の様になっており、(横軸が$x$軸、縦軸が$t$軸。)
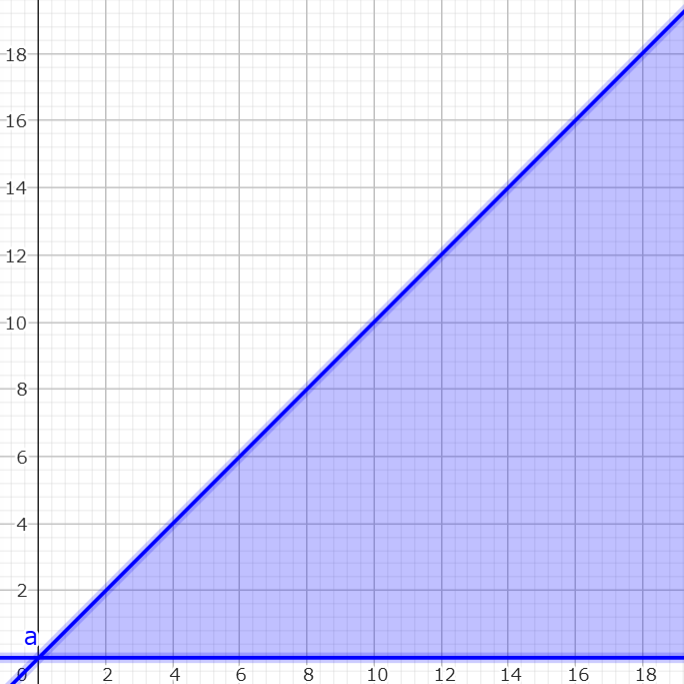積分範囲
これは、$x$が$0$から$t$までを動いて、$t$が$0\to \infty$と動く
とも捉えられる。よって、
$$\int_0^\infty\left(\int_0^t x^{a-1}(t-x)^{b-1}e^{-t}\: dx\right)\: dt$$
最後に、$x$に対して、$x=tz$と変数変換すると、$x:0\to t$で$z:0\to 1$であり、$\dfrac{dx}{dz} = t$であるから、
$$\int_0^\infty \left(\int_0^1 t^{a+b-2}e^{-t}z^{a-1}(1-z)^{b-1}\: t\: dz\right)\: dt$$
$$\int_0^\infty t^{a+b-1}e^{-t}\: dt \int_0^1 z^{a-1}(1-z)^{b-1}\: dz$$
$$= \Gamma(a+b)B(a,b)$$
よって、$B(a,b) = \dfrac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}$

$$B\left(\dfrac{1}{2},\dfrac{1}{2}\right) = \dfrac{\Gamma\left(\dfrac{1}{2}\right)^2}{\Gamma(1)} = \Gamma\left(\dfrac{1}{2}\right)^2$$
$$B\left(\dfrac{1}{2},\dfrac{1}{2}\right) = 2\int_0^{\frac{\pi}{2}}d\theta = \pi$$
整理して両辺平方根を取ると、$\displaystyle \Gamma\left(\dfrac{1}{2}\right) = \sqrt{\pi}$

$f(x) = \dfrac{2^{x-1}}{\sqrt{\pi}}\Gamma\left(\dfrac{x}{2}\right)\Gamma\left(\dfrac{x+1}{2}\right)$とするとき、$f(x)=\Gamma(x)$となることを示せばよい。
\begin{eqnarray*} f(x+1) &=& \dfrac{2^x}{\sqrt{\pi}}\Gamma \left(\dfrac{x+1}{2}\right)\Gamma\left(\dfrac{x}{2}+1\right)\\ &=& \dfrac{2\cdot 2^{x-1}}{\sqrt{\pi}}\Gamma \left(\dfrac{x+1}{2}\right)\dfrac{x}{2}\Gamma\left(\dfrac{x}{2}\right)\\ &=& xf(x) \end{eqnarray*}
また、$x>0$のとき$f(x)>0$で、
$$\log f(x) = (x-1)\log 2 -\log \sqrt{\pi} + \log \Gamma \left(\dfrac{x}{2}\right) + \log \Gamma \left(\dfrac{x+1}{2}\right)$$
であるから、
$$\{\log f(x)\}'' = \left\{\log \Gamma \left(\dfrac{x}{2}\right)\right\}'' + \left\{\log \Gamma \left(\dfrac{x+1}{2}\right)\right\}'' \geqq 0$$
となる。そして、$f(1) = \dfrac{1}{\sqrt{\pi}}\cdot 1\cdot \sqrt{\pi} =1$であるから、3条件を満たすので、
$f(x) = \Gamma (x)$である。

$0< x<1$に対して、
$$f(x) = \Gamma(x)\Gamma(1-x)\sin \pi x$$
を定める。この関数を$x=0,1$でも定義できるようにする。
\begin{eqnarray*}   f (0) &=& \lim_{x\rightarrow 0}\Gamma (x+1)\Gamma (1-x)\dfrac{\sin \pi x}{x}\\  &=& \lim_{x\rightarrow 0}\Gamma \pi(x+1)\Gamma (1-x)\dfrac{\sin \pi x}{\pi x}\\  &=& \pi \cdot 0!\cdot 0!\qquad \left(\because \lim_{x\rightarrow 0}\dfrac{\sin x}{x} = 1\right)\\  &=& \pi \end{eqnarray*}
また、
\begin{eqnarray*}   f(1) &=& \lim_{x\rightarrow 1}\Gamma (x)\Gamma(1-x)\sin \pi x\\   &=& \lim_{x\rightarrow 0} \Gamma (x+1)\Gamma(-x)\sin (\pi x + \pi)\\   &=& \lim_{x\rightarrow 0}x\Gamma(x)\dfrac{\Gamma(1-x)}{-x}(-\sin \pi x)\\   &=& \lim_{x\rightarrow 0}\Gamma (x)\Gamma (1-x)\sin \pi x =f(0) \end{eqnarray*}
となるので、$f(0) = f(1) = \pi$

\begin{eqnarray*} f\left(\dfrac{x}{2}\right)f\left(\dfrac{x+1}{2}\right) &=& \Gamma\left(\dfrac{x}{2}\right)\Gamma \left(1-\dfrac{x}{2}\right)\sin \dfrac{\pi x}{2}\Gamma \left(\dfrac{x+1}{2}\right)\Gamma\left(\dfrac{1-x}{2}\right)\sin \left(\dfrac{\pi x}{2}+\dfrac{\pi}{2}\right)\\ &=& \Gamma \left(\dfrac{x}{2}\right)\Gamma \left(\dfrac{x+1}{2}\right)\Gamma\left(\dfrac{1-x}{2}\right)\Gamma \left(1-\dfrac{x}{2}\right)\sin \dfrac{\pi x}{2}\cos \dfrac{\pi x}{2}\\ \end{eqnarray*}
公式1の事実を用いれば、これはさらに変形出来て、
\begin{eqnarray*}   &=& \dfrac{\sqrt{\pi}}{2^{x-1}}\Gamma (x) \sqrt{\pi}2^x\Gamma (1-x)\dfrac{1}{2}\sin \pi x\\   &=& \pi\Gamma (x)\Gamma(1-x)\sin \pi x\\   &=& \pi f(x) \end{eqnarray*}
$g(x) = \left\{\log f(x)\right\}''$とおく。
$$g(x) = \left\{\log\left[\dfrac{1}{\pi}f\left(\dfrac{x}{2}\right)f \left(\dfrac{x+1}{2}\right)\right]\right\}'' = \dfrac{1}{4}\left\{g\left(\dfrac{x}{2}\right)+ g\left(\dfrac{x+1}{2}\right)\right\}$$
$|g(x)|$の最大値を$M$とおけば、
$$|g(x)|\leqq \dfrac{1}{4}\left|g\left(\dfrac{x}{2}\right)\right|+\dfrac{1}{4}\left|g\left(\dfrac{x+1}{2}\right)\right| \leqq \dfrac{M}{4}+\dfrac{M}{4} = \dfrac{M}{2}$$
となるので、$M$の存在が矛盾しないためには、$M=0$と取るほかない。
絶対値を取って最大が0であるということは、$g(x)$は常に0でなければならない。

$\{\log f(x)\}''$が常に0ということは、$\log f(x)$は定数関数か一次関数であることになるが、$f(0) = f(1)$であるので、定数関数となる。$\log f(x)$が定数であるので、$f(x)$は定数。つまり$f(x)= \pi$
よって相反公式が得られる。