マス目に数を書き込んだときの隣接する数の和

100

数学力のなさ

　私が作問しOMCに出題された以下の問題について、一般化を考えたい。

OMC027-B

$3 \times 3$のマス目に$1$以上$9$以下の整数を$1$つずつ書き込みます。このとき、どの隣り合う$2$マスについても、数の和が$11$以下となるような書き込み方は$M$通りあります。$M$を解答してください。ただし、回転や反転で一致するものも区別するものとします。
（ https://onlinemathcontest.com/contests/omc027/tasks/3 より）

　$11$という数は、限界の値である。つまり、これを$10$にすることはできない。どのマスも少なくとも$2$つのマスと隣接しており、$9$と隣接する数を考えれば、和の最大値は$11$以上にならざるを得ないからである。
　では、$n \times n$ではこの限界の値はどうなるか。次が成り立ちそうである。

$n \times n$のマス目に$1$から$n^{2}$までの整数を$1$つずつ書き込むとき、隣り合う$2$マスの数の和の最大値としてありうる最小値は、$n^{2}+ \lfloor \dfrac{n}{2} \rfloor +1 $である。すなわち、どの隣り合う$2$マスについても数の和が$n^{2}+ \lfloor \dfrac{n}{2} \rfloor +1 $以下となる書き込み方は存在するが、どの隣り合う$2$マスについても数の和が$n^{2}+ \lfloor \dfrac{n}{2} \rfloor $以下となる書き込み方は存在しない。

$n^{2}+ \lfloor \dfrac{n}{2} \rfloor +1 $のときは、以下のように数を書き込んでいけばよい。(図は$n=9$のとき)
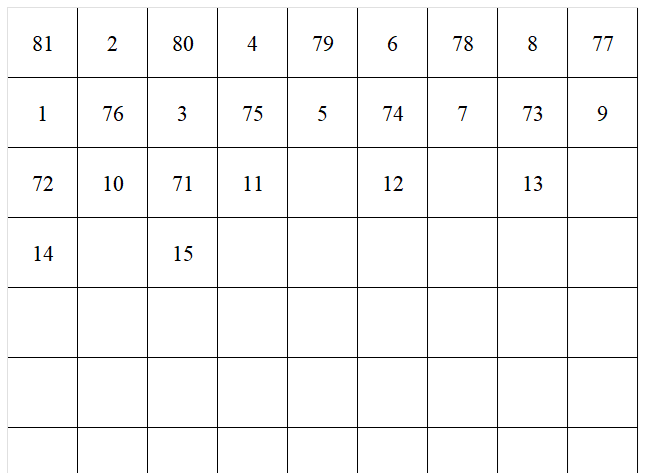左上から大きい数と小さい数を交互に埋めていく

あとは$n^{2}+ \lfloor \dfrac{n}{2} \rfloor $が無理であることを証明すればよいが……。証明が思いつかないので、置いとこう。

　最初のOMC問題の一般化としては、次の問題を解くことが一旦の目標となる。

一般化 $n \times n$

$n \times n$のマス目に$1$以上$n^{2}$以下の整数を$1$つずつ書き込む。このとき、どの隣り合う$2$マスについても、数の和が$n^{2}+ \lfloor \dfrac{n}{2} \rfloor +1 $以下となるような書き込み方は何通りあるか。ただし、回転や反転で一致するものも区別するものとする。

$n=4$のときを実際に求めてみよう。

4×4雑解説

　$16,15$の位置関係で場合分けを行う。★は$1,2,3,4$のいずれかを表す。
(14,5),(13,6),…を順にはめ込んでいく方法を考えると、数えられる

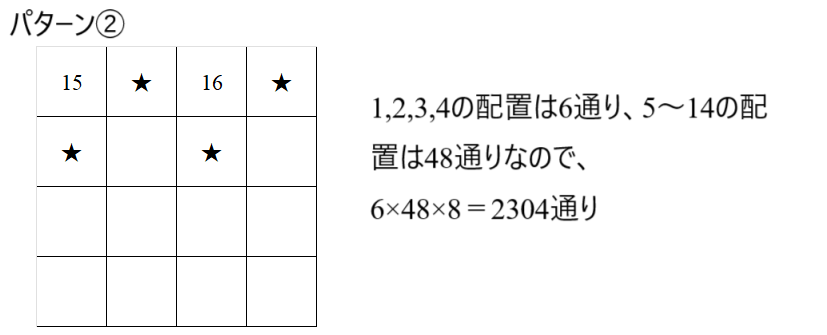
以上により、合計は$11520$通りである。

一般化検討

　$n \times n$のときも$4 \times 4$と同様に、最初のいくつかの数を与えておけば、あとは$2 \times 1$の長方形で埋める方法を数えていけばよい。が、結局場合分けが大量発生するような気がする……。よくわからん。

もっと一般化できるくね？

$a_{1} \times a_{2} \times \cdots \times a_n$

　$a_{1} \times a_{2} \times \cdots \times a_n$の$n$次元直方体のマス目に$1$以上$a_{1} a_{2} \cdots a_n$以下の整数を$1$つずつ書き込む。このとき、どの隣り合う$2$マスについても、数の和が$N$以下となるような書き込み方は何通りあるか。ただし、回転や反転で一致するものも区別するものとする。

　$3$次元の一番簡単な場合だけやってみる。$2 \times 2 \times 2$で、$N=11$とする。
　$8$の場所が$8$通り、$1,2,3$の場所が$6$通り、$7$と$4$の場所が$3$通り、$5$と$6$の場所が$2$通りなので、$8 \times 6 \times 3 \times 2 = 288$通り。