自分なりのカークマンシステム
前に記事を書いたシュタイナートリプルシステムシステムは
$n^{2}+n+1$人から$n+1$人ずつのグループを作り、
自分以外の全員に対して、同じ人と一度しか組まない組み合わせです。
今回はコレを分解可能にできるカークマントリプルシステムの組み立て方を紹介してみたいと思います。
カークマントリプルシステム
シュタイナーシステムが有限射影平面を基にしてるのに対して
カークマンシステムは有限アフィン平面を基にしています。
私が今回記事に書く射影平面、アフィン平面は共にデザルグ平面と呼ばれています。他にも非デザルグ平面と呼ばれるものが数種類ありますが、ここでは長くなるのでやめときます。
しかしアフィン平面ならば射影平面に変換できます。
今回紹介するカークマンシステムは
$p^{2}$人から$p$人ずつの$p$個のグループを$p+1$個に分解できます。
因みに$p$は素数です。
本当は素数じゃなくてもできる場合があるのですが、その場合の一般的な組み立て方法も証明もわかりません。
なので位数が素数の場合の条件付きで今回私が発見した作成方法を書きたいと思います。
まず$p$の平方形のブロックに$1$から$p^{2}$までの数字を入れて、左上の$1$を中心に縦と横と斜めの直線で引いた数をグループとします。
$0$列$0$行から$(p-1)$列$(p-1)$行の$p$のブロック。※横(行→)$y$、 縦(列↓)$x$とします。
$【p^{2}ブロック】p=5$の場合、
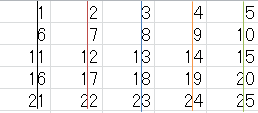 縦
縦
${1,6,11,16,21}$
${2,7,12,17,22}$
${3,8,13,18,23}$
${4,9,14,19,24}$
${5,10,15,20,25}$
 横
横
${1,2,3,4,5}$
${6,7,8,9,10}$
${11,12,13,14,15}$
${16,17,18,19,20}$
${21,22,23,24,25}$
そして残りの数の斜めを引いていきます。
(斜めだと途中で数が足りなくなるので、$p^{2}$ブロックを横に足していきます)
※実際にブロックデザインを作成するときは$p^{2}$ブロックの中だけで線を引く方が楽です。
![斜線!FORMULA[31][36913844][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fi0Z0dWb29qI5LVGJvbSS.png?alt=media) 斜線$y=x$
斜線$y=x$
${1,7,13,19,25}$
${2,8,14,20,21}$
${3,9,15,16,22}$
${4,10,11,17,23}$
${5,6,12,18,24}$
![斜線!FORMULA[37][1144264534][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FDNqX8atCz971odfd3Kjt.png?alt=media) 斜線$y=2x$
斜線$y=2x$
${1,8,15,17,24}$
${2,9,11,18,25}$
${3,10,12,19,21}$
${4,6,13,20,22}$
${5,7,14,16,23}$
![斜線!FORMULA[43][1144265495][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FEy7hajDAVSXHnkJ4tpnK.png?alt=media) 斜線$y=3x$
斜線$y=3x$
${1,9,12,20,23}$
${2,10,13,16,24}$
${3,6,14,17,25}$
${4,7,15,18,21}$
${5,8,11,19,22}$
![斜線!FORMULA[49][1144266456][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fio4dY9LfmrZiI4SPpNNT.png?alt=media) 斜線$y=4x$
斜線$y=4x$
${1,10,14,18,22}$
${2,6,15,19,23}$
${3,7,11,20,24}$
${4,8,12,16,25}$
${5,9,13,17,21}$
縦横の$2$と角度別の斜線$p-1$を足して$p+1$個に分解できます。
図を見てわかる通り縦横は一目瞭然ですが、
斜めでは何故ほかの数字と被らないか気になります。
斜線が他と被らず線が当たるか自分なりに証明しました。
斜線の傾きの違いにより、素数の特性を使い、ブロックごとに被りません。
$(p-1)^{2}$のブロックを作ります。
$1列目$$(y=x)$,$2列目$$(y=2x)$〜$(p-1)列目$$(y=(p-1)x)$
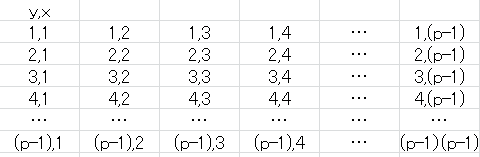 倍数ごとの角度違いの斜線
倍数ごとの角度違いの斜線
もし列と行で$x$と$y$の乗算が同じになるとグループ内で被る。
$y×x$にすると、
 九九の表
九九の表
九九の表になるため左上からの斜線を基準に対称になる。よって同値になる可能性は斜めにある値であって、縦、横の値は被らない。
素数は$1$から$p-1$までの数の$a$に対して互いに素なので
完全剰余系の基本定理により
$p$を法とすると余りが全て異なる数になり、
縦横の数字が異なるラテン方格になります。
![!FORMULA[72][36643648][0]の場合](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FK6o5qtwcj7yJcDsLnCG9.png?alt=media) $p=5$の場合
$p=5$の場合
よって倍数により角度の違う
(p-1)個の斜線すべてで異なることが分かります。
一番左上のマスの$1$から斜線を引き下ろす場合、
$1$行目すべてに$1$を挿入して他の行目に$1$を足す。
![!FORMULA[77][36643648][0]斜線のブロック](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fm7VwTjZifNAFcLgAghJx.png?alt=media) $p=5$斜線のブロック
$p=5$斜線のブロック
これを各倍数(列)ごとの$1$から$p$までの斜線の場合全て引き下す。
つまり$p^{2}$ブロック内で一番左上のマスから$y=x$から$y=x(p-1)$までの傾きの線を引いて、当たった数でブロックを組めば、アフィン平面のブロックデザインが作成できます。
この斜線のブロックの列の並びがグループになります。
これら斜線のブロックに縦横の直線$2$つを足して
$p^{2}$を$p$個の$p$グループを$p+1$個に分解でき、同じものと一度しか組まない方法が証明できました。
a、n が互いに素であるとするとき、n−1個の相異なる整数
1a、2a、3a、· · ·、(n −1)a
をnで割った余りは、1 からn-1までの全ての整数が
1回ずつすべて (順不同で) 現れる。
射影平面への変換
アフィン平面に一本の線上$p+1$の点を足して$p^{2}+p+1$射影平面になります。
縦横斜めのブロック毎に$p+1$の点を追加します。そして追加の点による線も追加したら完成です。
先程の$【p^{2}ブロック】p=5$のアフィン平面を使う。
縦
${1,6,11,16,21,26}$
${2,7,12,17,22,26}$
${3,8,13,18,23,26}$
${4,9,14,19,24,26}$
${5,10,15,20,25,26}$
横
${1,2,3,4,5,27}$
${6,7,8,9,10,27}$
${11,12,13,14,15,27}$
${16,17,18,19,20,27}$
${21,22,23,24,25,27}$
斜線$y=x$
${1,7,13,19,25,28}$
${2,8,14,20,21,28}$
${3,9,15,16,22,28}$
${4,10,11,17,23,28}$
${5,6,12,18,24,28}$
斜線$y=2x$
${1,8,15,17,24,29}$
${2,9,11,18,25,29}$
${3,10,12,19,21,29}$
${4,6,13,20,22,29}$
${5,7,14,16,23,29}$
斜線$y=3x$
${1,9,12,20,23,30}$
${2,10,13,16,24,30}$
${3,6,14,17,25,30}$
${4,7,15,18,21,30}$
${5,8,11,19,22,30}$
斜線$y=4x$
${1,10,14,18,22,31}$
${2,6,15,19,23,31}$
${3,7,11,20,24,31}$
${4,8,12,16,25,31}$
${5,9,13,17,21,31}$
追加した点による線
${26,27,28,29,30,31}$
カークマンの話
カークマントリプルシステムを作ったイギリス人数学者トーマス・カークマンは、実は最初にシュタイナートリプルシステムを作った人でもあります。
しかし、名前が売れておらずスイス人数学者ヤコブ・シュタイナーが再発見したことにより名前が付けられました。さらにカークマンは同国の有名数学者アーサー・ケイリーやジェームス・ジョセフ・シルベスターと折り合いが悪く、シルベスターが「この分野を作った」と主張しカークマンの業績を横取りするような事もありました。
カークマンの女学生問題
今回記事にしたのは$p^{2}$人から$p$人のグループを$p$個作り、$p+1$に分けることでした。
カークマンが作った最初の問題は$15$人の女学生は$3$人を$5$つのグループを作り、$7$日間に分けるとき、毎日$1$回だけ一緒に登下校する組合せを考えろという問題でした。現在これは一般化し$15$人ではなく$6n+3$人となっています。
これも悲しい話ですが、一般化した女学生の問題はインド系アメリカ人数学者$2$人が証明しましたが、その数年前に中国人アマチュア数学者が証明していました。しかし論文を中国科学院数学研究所が「基本的に新しい結果ではなく、価値がない」という文言と一緒に不受理になりました。数年後価値に気付いて本人に賞を与えましたが、その時は教師以外でも仕事をし重労働で体に限界がきていて、$48$歳で息を引き取りました。ちなみに死後二日後にカナダのトロント大学からのお誘いのメールが届きました。
アーベル的悲劇です。
追記
一般カークマントリプルシステムは頂点の数が$6n+3$であれば必ず成り立つことを示しています。しかしそれを作成する決まりの方法が無かったので、この素数位数のカークマンシステムの作成方法を応用して頂点の数が$3^{m}$以上のアフィン空間になる場合のみの作り方を書こうと思います。
完全剰余系の基本定理で素数の累乗$p^{m} $が$aから(p-1)a$の$a$に対しても互いに素なのは明らかです。
$p$を素数として
$(1行目)=1…(p^{n}-1)=(1とp^{n}は互いに素)$ $(2行目)=2(1…(p^{n}-1))=(2とp^{n}は互いに素)$ $(3行目)=3(1…(p^{n}-1))=(3とp^{n}は互いに素)$ $………$$(p-1行目)=(p-1)(1…(p^{n}-1))$まで続ける。$p$は$p^{n}$の約数なので$(p-1)$行目に抑える。
列の数は斜線に対称なので被らない。
これで縦p横p^{n}の斜線ブロックが作れる。
カークマンシステムの元になる
アフィン平面$3^{2}$の縦3横3
〇〇〇 〇〇〇 〇〇〇
〇〇〇 〇〇〇 〇〇〇
〇〇〇 〇〇〇 〇〇〇
123 101112 192021
456 131415 222324
789 161718 252627
の頂点に縦横に線を引きそして斜線は上で示した九九の表を用いた方法で示せますが、縦3横9
〇〇〇〇〇〇〇〇〇
〇〇〇〇〇〇〇〇〇
〇〇〇〇〇〇〇〇〇
の場合は縦線と斜線はできても横線ができません。
しかし通常の位数$3$アフィン平面の頂点の数である$3^{2}$の数を利用して、1段目、2段目、3段目の三か所に置くとします。
そして数字をはめて
⑴⑵⑶⑷⑸⑹⑺⑻⑼
⑽⑾⑿⒀⒁⒂⒃⒄⒅
⒆⒇㉑㉒㉓㉔㉕㉖㉗
として、上で示した方法で作成すると
縦線
$ 1,10,19-2,11,20-3,12,21-4,13,22-5,14,23-6,15,24-7,16,25-8,17,26-9,18,27$
斜線y=x
$ 1,11,21-2,12,22-3,13,23-4,14,24-5,15,25-6,16,26-7,17,27-8,18,19-9,10,20$
斜線y=2x
$1,12,23-2,13,24-3,14,25-4,15,26-5,16,27-6,17,19-7,18,20-8,10,21-9,11,22$
斜線y=3x
$1,13,25-2,14,26-3,15,27-4,16,19-5,17,20-6,18,21-7,10,22-8,11,23-9,12,24 $
斜線y=4x
$1,14,27-2,15,19-3,16,20-4,17,21-5,18,22-6,10,23-7,11,24-8,12,25-9,13,26$
斜線y=5x
$1,15,20-2,16,21-3,17,22-4,18,23-5,10,24-6,11,25-7,12,26-8,13,27-9,14,19$
斜線y=6x
$1,16,22-2,17,23-3,18,24-4,10,25-5,11,26-6,12,27-7,13,19-8,14,20-9,15,21$
斜線y=7x
$1,17,24-2,18,25-3,10,26-4,11,27-5,12,19-6,13,20-7,14,21-8,15,22-9,16,23$
斜線y=8x
$1,18,26-2,10,27-3,11,19-4,12,20-5,13,21-6,14,22-7,15,23-8,16,24-9,17,25$
横線(アフィン平面$3^{2} $縦線)
$1,4,7-2,5,8-3,6,9-10,13,16-11,14,17-12,15,18-19,22,25-20,23,26-21,24,27$
横線(アフィン平面$3^{2} $横線)
$1,2,3-4,5,6-7,8,9-10,11,12-13,14,15-16,17,18-19,20,21-22,23,24-25,26,27$
横線(アフィン平面$3^{2} $斜線y=x)
$1,5,9-4,8,3-7,2,6-10,14,18-13,17,12-16,11,15-19,23,27-22,26,21-25,20,24$
横線(アフィン平面$3^{2} $斜線y=2x)
$1,6,8-2,4,9-3,5,7-10,15,17-11,13,18-12,14,16-19,24,26-20,22,27-21,23,25$
と表わせます。
この結果を
縦3横27
$〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇$
$〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇$
$〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇〇$
$⑴⑵⑶⑷⑸⑹⑺⑻⑼⑽⑾⑿⒀⒁⒂⒃⒄⒅⒆⒇㉑㉒㉓㉔㉕㉖㉗$
$㉘㉙㉚㉛㉜㉝㉞㉟㊱㊲㊳㊴㊵㊶㊷㊸㊹㊺㊻㊼㊽㊾㊿………54$
$55565758596061626364656667686970717273…………81$
に、この横並びの数字対して先程示した縦3横3、それを基に縦3横9のカークマンシステムを使う。
$p^{n}$個のアフィン空間の横線(横並び頂点)のブロック作成の手順は、
⑴,$p^{2}$個に区切って行列にして、区切った各行列で$p^{2}$個アフィン平面を作る。
さらに各アフィン平面で同じ角度の直線同士のブロックを作る。
⑵,$p^{3}$個に区切って列(縦)$p$行(横)$p^{2}$の行列を作り、真下(縦線)と角度別斜めの線を引く。
各行列で同じ角度の直線同士のブロックを作る。
⑶,⑵と同じ作業を列(縦)$p$行(横)$p^{n-1}$個の行列まで繰り返します。
⑷,$p^{2}$の行列(アフィン平面)から$p^{n-1}$の行列にかけて作った、同じ角度の直線同士のブロックが列(縦)$p$行(横)$p^{n}$のアフィン空間の各行のアフィン空間のブロックデザインです。
縦pは固で横並びの数字が$3^{m}$づつ増えます。
射影空間に変換
射影空間$ p^{n}+p^{n-1}+p^{n-2}+…+p^{2}+p^{1}+1$に変換するには
$n$次元アフィン空間$【p^{n}】$に一つの$(n-1)$次元射影空間$【p^{n-1}+p^{n-2}+…+p^{2}+p^{1}+1】$を挿入する事です。これも射影平面から$n$次元射影空間のブロックデザインを再帰的に作成できるのがわかります。※しかしシュタイナーシステムであってカークマンシステム(分割可能なシュタイナーシステム)ではない。
$ 3^{3}$に$ 3^{2}+3+1$を足す。
まずは先程の位数$3$の$3^{3}$アフィン空間を使います。
縦線
$ 1,10,19,28-2,11,20,28-3,12,21,28-4,13,22,28-5,14,23,28-6,15,24,28-7,16,25,28,28-8,17,26-9,18,27,28$
斜線y=x
$ 1,11,21,29-2,12,22,29-3,13,23,29-4,14,24,29-5,15,25,29-6,16,26,29-7,17,27,29-8,18,19-9,10,20,29$
斜線y=2x
$1,12,23,30-2,13,24,30-3,14,25,30-4,15,26,30-5,16,27,30-6,17,19,30-7,18,20,30-8,10,21,30-9,11,22,30$
斜線y=3x
$1,13,25,31-2,14,26,31-3,15,27,31-4,16,19,31-5,17,20,31-6,18,21,31-7,10,22,31-8,11,23,31-9,12,24,31 $
斜線y=4x
$1,14,27,32-2,15,19,32-3,16,20,32-4,17,21,32-5,18,22,32-6,10,23,32-7,11,24,32-8,12,25,32-9,13,26,32$
斜線y=5x
$1,15,20,33-2,16,21,33-3,17,22,33-4,18,23,33-5,10,24,33-6,11,25,33-7,12,26,33-8,13,27,33-9,14,19,33$
斜線y=6x
$1,16,22,34-2,17,23,34-3,18,24,34-4,10,25,34-5,11,26,34-6,12,27,34-7,13,19,34-8,14,20,34-9,15,21,34$
斜線y=7x
$1,17,24,35-2,18,25,35-3,10,26,35-4,11,27,35-5,12,19,35-6,13,20,35-7,14,21,35-8,15,22,35-9,16,23,35$
斜線y=8x
$1,18,26,36-2,10,27,36-3,11,19,36-4,12,20,36-5,13,21,36-6,14,22,36-7,15,23,36-8,16,24,36-9,17,25,36$
横線(アフィン平面$3^{2} $縦線)
$1,4,7,37-2,5,8,37-3,6,9,37,37-10,13,16,37-11,14,17,37-12,15,18,37-19,22,25,37-20,23,26,37-21,24,27,37$
横線(アフィン平面$3^{2} $横線)
$1,2,3,38-4,5,6,38-7,8,9,38-10,11,12,38-13,14,15,38-16,17,18,38-19,20,21,38-22,23,24,38-25,26,27,38$
横線(アフィン平面$3^{2} $斜線y=x)
$1,5,9,39-4,8,3,39-7,2,6,39-10,14,18,39-13,17,12,39-16,11,15,39-19,23,27,39-22,26,21,39-25,20,24,39$
横線(アフィン平面$3^{2} $斜線y=2x)
$1,6,8,40-2,4,9,40-3,5,7,40-10,15,17,40-11,13,18,40-12,14,16,40-19,24,26,40-20,22,27,40-21,23,25,40$
そこに位数$3$の次元$2$の射影空間(射影平面)$ 3^{2}+3+1 $を追加します。
$28,29,30,37-31,32,33,37-34,35,36,37-28,31,34,38-29,32,35,38-30,33,36,38-28,32,36,39-29,33,34,39-30,31,35,39−28,33,35,40−
29,31,36,40−30,32,34,40$
$37,38,39,40$
カークマンの女学生問題は位数2、次元3の射影空間と同じ数だと証されました。
今回紹介した方法で示してみます。
まず位数2,次元3のアフィン空間のブロックデザインを作ります。
$1,2,3,4$
$5,6,7,8$
まず真下、各斜めの線
$1,5-2,6-3,7-4,8$
$1,6-2,7-3,8-4,5$
$1,7-2,8-3,5-4,6$
$1,8-2,5-3,6-4,7$
そして横の線を構築するため、次元を1つ下げたアフィン空間を作る。
(1段目の2^2と2段目の2^2によるアフィン平面)
$1,2$ $5,6$
$3,4$ $7,8$
$1,2-3,4-5,6-7,8$
$1,3-2,4-5,7-6,8$
$1,4-2,3-5,8-6,7$
上で示した位数2、次元3のアフィン空間を射影空間にします。
$2^3$に$(2^2+2+1)$を足します。
まずは$2+1$にするために、各線に各点1つを足していきます。
$1,2,9-3,4,9-5,6,9-7,8,9$
$1,3,10-2,4,10-5,7,10-6,8,10$
$1,4,11-2,3,11-5,8,11-6,7,11$
$1,5,12-2,6,12-3,7,12-4,8,12$
$1,6,13-2,7,13-3,8,13-4,5,13$
$1,7,14-2,8,14-3,5,14-4,6,14$
$1,8,15-2,5,15-3,6,15-4,7,15$
さらに$2^2+2+1$の射影平面を足します。
$9,10,12-10,11,13-11,12,14-12,13,15-13,14,9-14,15,10-15,9,11$
