前田数学模試(中1)

前田数学模試(Level中1)
試験時間・・・50分

大問1 (25点)
次の式を計算せよ.
(1)$(-3)^2÷(\frac{3}{7})^2-3^2÷\frac{3}{7}+(-3)^2÷(-\frac{3}{7})^3$
(2)$\frac{x-1}{3}+\frac{x+1}{5}-\frac{x-1}{15}$
(3)円周率を$π$とするとき、直径$r$cmの面積と円周を求めよ。
(4)1辺の長さ$x$cmの立方体の体積と、表面積、周の長さを求めよ.
(5)$5x-2=\frac{1}{3}(6x+12)$の$x$の値を求めよ。
(1)~(5)各5点
※(3),(4)は完答

大問2 (25点)
(1)直線上をAさんが$1m/s$で3分歩いたあと、Bさんが$5.0m/s$で自転車で追いかけるとき、追いつくときの方程式をかけ。
(2)(1)の方程式を解け.
(3)AさんとBさんが(1)と同じ速さで半径40mの円周上を開始地点、向きは同じで動くときBさんがAさんに1周差,2周差,n周差のときの時間をもとめよ.
(1)・・・5点
(2)・・・5点
(3)・・・各5点

大問3(25点)
(1)
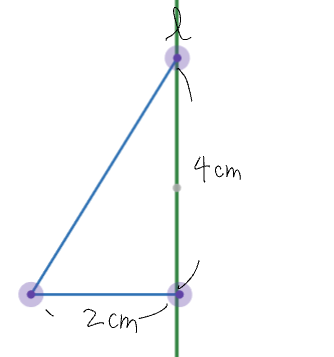
図1の図形を$l$軸を回転した体積を求めよ。また、単位は$cm^3$で答えよ.
(2)図1の図形を90°ごとに360°回転させたときの体積を求めよ。また、体積は$cm^3$で答えよ。
(3)
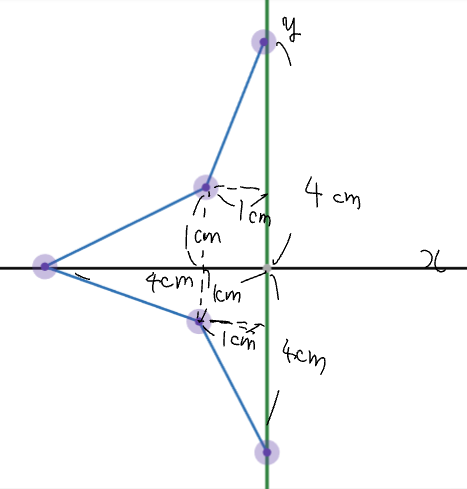
(a)$x$軸を回転させたときの体積を求めよ。ただし、単位は$cm^3$で答えよ。
(b)$y$軸を回転させたときの体積を求めよ。ただし、単位は$cm^3$で答えよ。
(1)・・・各2点
(2)・・・6点
(3)
(a)・・・7点
(b)・・・8点

大問4(25点)
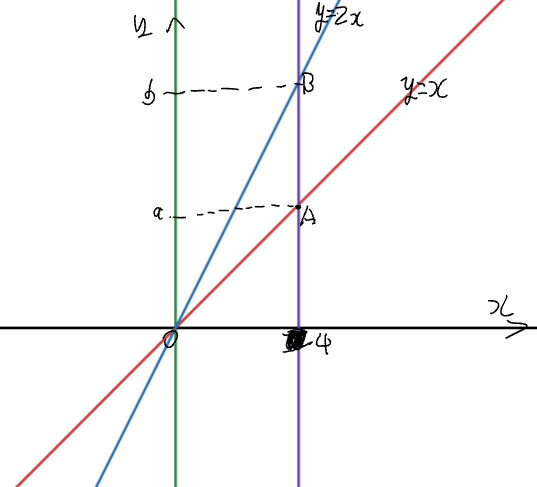大問4
(1)$a,b$の値を求めよ.
(2)$\triangle{OAB}$の面積を求めよ。
(3)円周率をπとする。
(a)$x$軸を軸として、$\triangle{OAB}$を回転させたときの体積を求めよ。
(b)$y$軸を軸として、$\triangle{OAB}$を回転させたときの体積を求めよ。
(1)・・・各2点
(2)・・・6点
(3)
(a)・・・7点
(b)・・・8点