【射影幾何】1.1 基礎
1.1 基礎
射影幾何を学ぶ前に、そもそも幾何って何?という問から始めようと思います.要するに基礎固めといったところです.一般論であるため抽象度は高いですが,ゆっくりと一歩ずつ進んでいきましょう.
集合$\Omega$と次の(1),(2)を満たした$\Omega$上の関係$I$があるとき
(1)反射律 $\forall x\in I,xIx$
(2)対称律 $xIy \Rightarrow yIx$
この対$(\Omega,I)$のことを幾何(Geomtry)という.
この定義の意味を具体例を用いて考えてみましょう.
以下の図1を見てください.
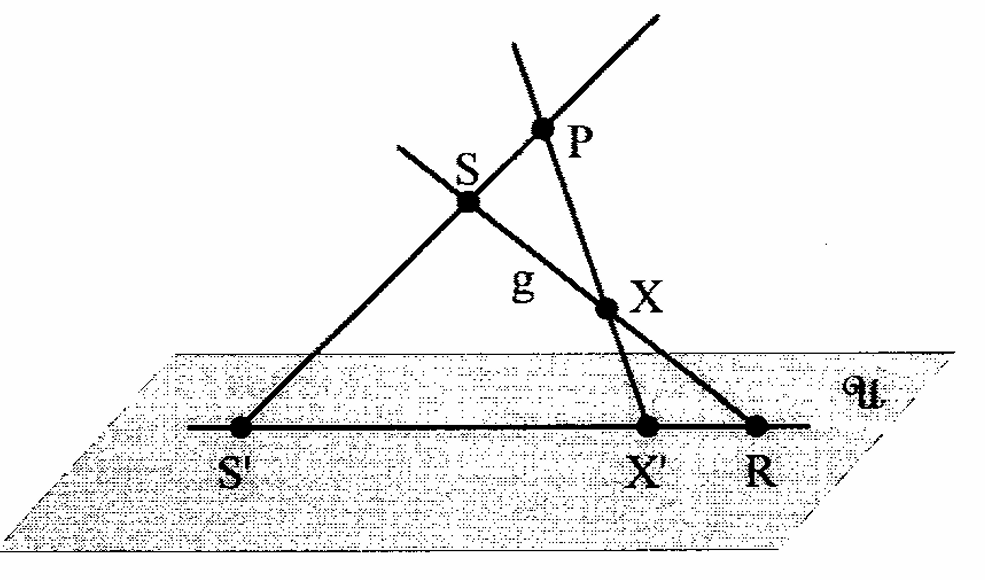
幾何というものは点(point),直線(line),平面(plane)がどういう繋がりを持っているのかを扱います.つまり図1でいうと「点$S,X,R$は直線$g$上にある.」や「平面$\mathscr{U}$上に点$S',X',R$がありそれらが同一直線状に並んでいる.」.こんなことを数学的に表現したいということです.この図に関していえば$\Omega=\{P,S,R,X,S',X',g,\mathscr{U}\}$で$I$は包含関係のことです.
あれ?包含関係は対称律を満たさないけど...
と思いつく方もいると思いますが、この包含関係は特殊なもので対称律を満たすものとします.つまり,
$xIy :\Longleftrightarrow (x\subset y) \lor (y\subset x)$
これを特に接続関係(incidence relation)と呼び,(つながっていることを表すもの)多くの幾何の場面では,この接続関係を$I$として考えます.
さて,図1の$\Omega$には点,直線,平面が一緒くたになっています.しかし,一緒になっているからと言って性質が同じなわけではありません.ここでそれらを区別するために次の概念を導入します.
$G=(\Omega,I)$を幾何とする.$\Omega$の部分集合$\mathcal{F}$を取る.これが
$\forall x,y\in F, xIy$
を満たすとき,$\mathcal{F}$を旗(flag)と呼ぶ.
また,任意に$x\in\Omega\setminus\mathcal{F}$を取り $\mathcal{F} \cup \{x\}$が旗にならないとき
$\mathcal{F}$を極大旗(maximal flag)と呼ぶ.
$G=(\Omega,I)$を幾何とする.
$\Omega$が$\Omega_1,\cdots,\Omega_r$と直和分割され,任意の$G$の極大旗$\mathcal{F}$を取り,
$|\Omega_i \cap \mathcal{F}|=1$
となるとき
$G$の階数(rank)は$r$であるといい,$\Omega_i$のことを型$i$という.
具体例として馴染み深い幾何$\mathbb{R}^3$について考えましょう.
旗としては,次のようなものが考えられます.
$\{(1,2,0)\},\{(1,1,1),x=y=z\},\{(1,1,1),x=y=z,y=z\}$
定義から明らかに最後の1つのみが最大旗となることは分かります.
ここで,
$\Omega_1=\{(x,y,z)|x,y,z\in\mathbb{R}\}$
$\Omega_2=\{(x,y,z)|\alpha(x-a)=\beta(y-b)=\gamma(z-c),\alpha,\beta,\gamma,a,b,c\in\mathbb{R}\}$
$\Omega_3=\{ax+by+cz+d=0|a,b,c,d\in \mathbb{R}\}$
(多少,書き方に厳密さが欠けます.)
と定めれば,これらは定義3を満たすため
この階数は3であることが分かります.
さて今まで出てきた定義などを確認するために次の簡単な補題を示してみましょう.
$G$を階数$r$の幾何とする.このとき
同じ型に属する異なる2つの要素は接続されない.
$x,y$を型$i$の要素,つまり$x,y \in \Omega_i$とする.ただし$x\not=y$.
このとき,$x,y$が接続してあると仮定する.
すると,この2つの要素を含む最大旗$\mathcal{F}$を考えることができる.
しかし,$|\Omega_i\cup\mathcal{F}| \geq 2$となりこれは$G$が階数$r$であることに矛盾する.
したがって,題意は示された.
次からの節では,最もシンプルな構造を持つ階数$2$の幾何について調べ,型$1$の集合の要素を点(point),型$2$の集合の要素をブロック(block)と呼び,それぞれを$\mathscr{P},\mathscr{B}$と書き表すことにします.(ブロックは直線のようなものと考えて良い.)
そして,これらの要素と単純な公理から成り立つ射影幾何を見ていこうと思います.
以上で,1.1基礎を終わりにしたいと思います!
まとめ
今日,出てきたキーワードは3つ!
"幾何"、"(極大)旗"、"階数"
おさらいをしておくと...
<幾何>
扱いたい対象$\Omega$及び,その対象の中でどれとどれが繋がっているのかを指し示す指標$I$の組($\Omega,I$)
<旗>
繋がりの単位,その中でも極大旗は考えうる繋がりの最大単位
<階数>
次元のようなもの
最後まで閲覧していただき,ありがとうございます!
間違いや分かりにくい部分がありましたら,ご遠慮なく指摘してください!
