OMC206(E)と群論+ちょっとした別解
OMC206 の以下の問題について考えます。
正$1234$角柱の頂点$2468$個それぞれを, 赤色, 青色, 緑色のうちから一つずつ選んで塗ります(使わない色が合っても構いません).ここで, 任意の辺に対して, その両端の$2$頂点の色が異なるようにします. そのような塗り方が$X$通りあるとき, $X$を素数$1237$で割った余りを求めて下さい.
ただし, 回転したり裏返したりして一致する塗り方も区別して考えます.
この問題の公式解説を見て、群論の知識を使えばちょっと深掘りできそうだなと思ったので、記事を書くことにしました。公式解説と少し異なる別解も見つかったので、紹介します。
群論を全く知らない方でもある程度伝わるように書いたつもりです。逆に、群論に詳しい方にとっては冗長な部分が多いと思います。あらかじめご了承ください。
以下、冒頭の問題の部分的な解説を含みます。
公式解説の方針
まず、公式解説がどのような方針で解いたかを見ます。最後までの解説はしませんので、全文を見たい方は冒頭のリンクから公式のものをお読みください。
公式解説と同じ記号を用います。一般に、正$n$角柱$P_1 \cdots P_n -Q_1 \cdots Q_n$で考えることとし、色の組
$$ (\text{赤},\text{青}), (\text{緑},\text{赤}), (\text{青},\text{緑}), (\text{青},\text{赤}),( \text{赤},\text{緑}), (\text{緑},\text{青})$$
をそれぞれ$A,B,C,D,E,F$とおきます。例えば$(P_i,Q_i)$の色が$A$だったとき、$(P_{i+1},Q_{i+1})$の色は$B,C,D$のいずれかです。
ここで、以下のような三角柱を考えます。
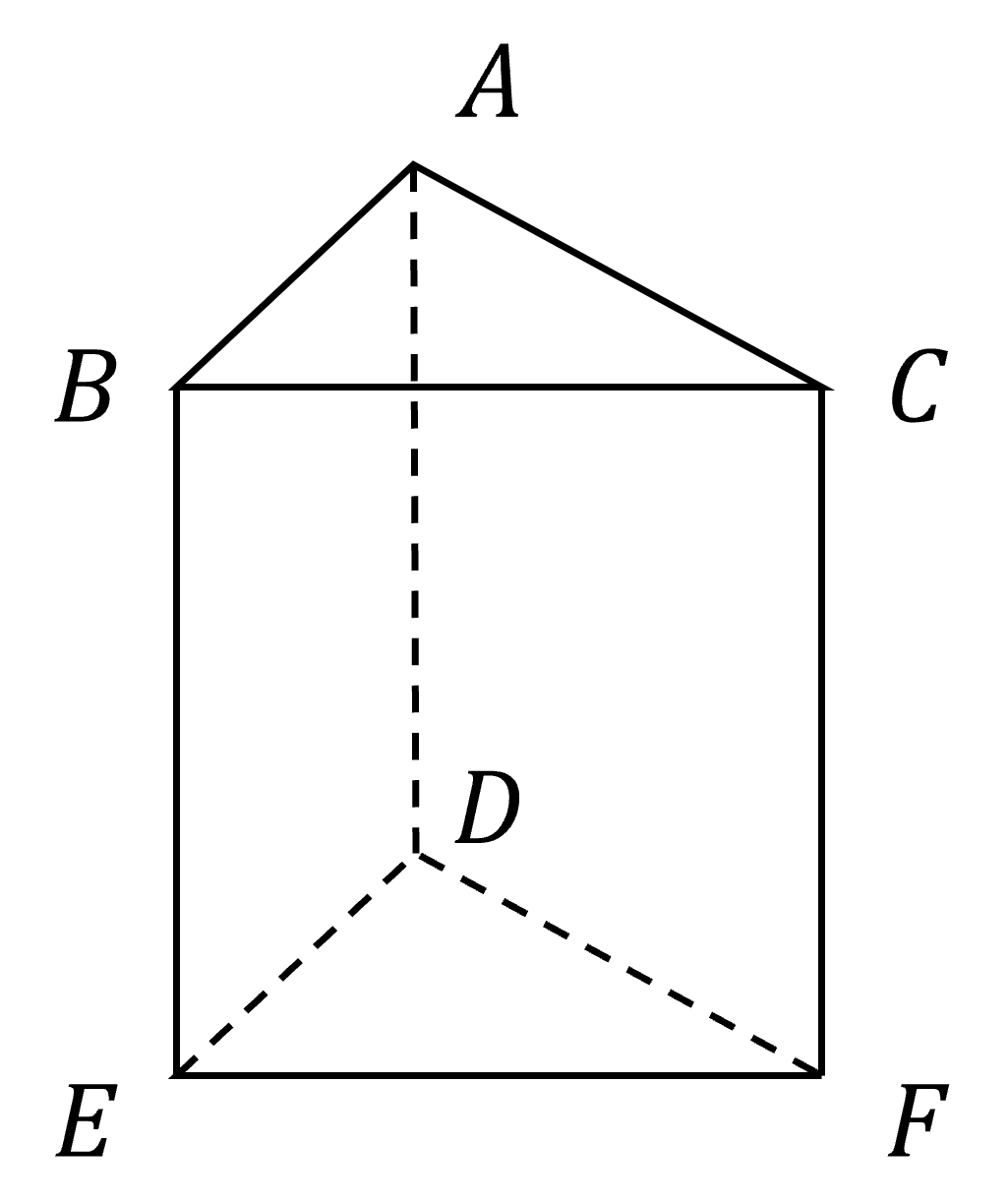
$(P_i,Q_i)$と$(P_{i+1},Q_{i+1})$の色の組としてあり得る組み合わせが、この三角柱の辺とちょうど一致しています(こういうのどうやって見つけるんでしょうね?)。
また、「$(P_i,Q_i)$の色が決まっている状態で$(P_{i+1},Q_{i+1})$の色を決定する」という操作を行うとき、色の組み合わせは最大18通りありますが、それらを次の3つに分類します。
$x$: $A \longrightarrow B, B \longrightarrow C, C \longrightarrow A, D \longrightarrow E, E \longrightarrow F, F \longrightarrow D$
$x^{-1}$: $A \longleftarrow B, B \longleftarrow C, C \longleftarrow A, D \longleftarrow E, E \longleftarrow F, F \longleftarrow D$
$y$: $A \longleftrightarrow D, B \longleftrightarrow E, C \longleftrightarrow F$
ここで、矢印の始点が$(P_i,Q_i)$の色、終点が$(P_{i+1},Q_{i+1})$の色を表します。$A \longleftrightarrow D$は$A \longrightarrow D$と$A \longleftarrow D$をまとめて書いたものです。三角柱の図で見ると、$x,x^{-1}$は回転、$y$は鏡映という操作になっていることが分かります(こういうのどうやって(略))。
例えば$(P_1,Q_1)$の色が$A$だったとき、問題の条件を満たすような色の塗り方を得るためには、$A$からスタートして$x,x^{-1},y$のいずれかの操作を$n$回行い、$n$回目の操作でまた$A$になるようなものを考えれば良いということになります。$n$回目の操作でまた$A$になるためには、$x$を行った回数が$3$の倍数(ただし、$x^{-1}$を$1$回行うことは$x$を$-1$回行うことと見なす)、$y$を行った回数が偶数であることが必要十分です。
このことから、多項式の係数の和を計算する問題に帰着させる、というのが公式解説の方針です。
$x$,$y$の性質
さて、先ほど「$n$回目の操作でまた$A$になるためには、$x$を行った回数が$3$の倍数、$y$を行った回数が偶数であることが必要十分」と書きましたが、これはなぜ成り立つのでしょうか。
もちろん、$x$は3回行うごとに元に戻る、$y$は2回行うごとに元に戻るということが効いているのですが、実はもう1つ重要な性質が隠れています。それは、$x$と$y$が可換であるということです。すなわち、$x$を行った後に$y$を行っても、$y$を行った後に$x$を行っても、結果は変わらないということです(確かめてみてください)。可換であるおかげで、$x$の回数と$y$の回数に分けて考えることができるのです。
式で表しましょう。$x$の後に$y$を施すことを$xy$のように書くことにします。
群論になじみのある方は書き順に違和感があるかもしれませんが、初見の方の読みやすさを優先してこのようにしています。
また、何の操作も行わないことを$1$で表します。2つの操作の結果が同じになるとき$=$で結ぶことにすると、ここまでで見つかった$x,y$の性質は
$(1)$ $xxx=1$
$(2)$ $yy=1$
$(3)$ $xy=yx$
と書くことができます。$x^3=1$などの書き方も用いることにします。
また、$x^{-1}$は$x^2$に等しいことが確かめられます。
$(4)$ $x^{-1}=xx=x^2$
$n$回の操作を行うことは、例えば
$$ xxyx^{-1}yx \cdots x^{-1}$$
のように、$x,x^{-1},y$を$n$個並べたものとして表すことができます。このような文字列に対し、以下のように公式を使ってみます。
① 公式(4)により、$x^{-1}$を$x^2$に変換する。
② 公式(3)により、$yx$を$xy$に変換する。これをくり返し行うと、最終的には$x^iy^j$の形になる。ここで、$x^0=y^0=1$と約束する。
③ 公式(1)(2)により、$x^3,y^2$を1に変換する。これにより、$x^iy^j \ \ (0 \leqq i \leqq 2, 0 \leqq j \leqq 1)$の形になる。
したがって、あらゆる操作は
$$ 1, \ x, \ x^2, \ y, \ xy, \ x^2y$$
のいずれかと同じ結果になります。なお、これら6つは相異なる操作になっています。例えば$A$の行き先を見ると確かめられます。
$n$回の操作で$A$が$A$に戻るということは、$x,x^{-1},y$を並べた長さ$n$の文字列を上のように変換したとき$1$になる、ということと同じです。
群論へ
さて、本格的に群の話に入っていきます。まず群の定義を書いておきますが、流し見程度でも(多分)大丈夫です。
集合$G$にある二項演算$* : G\times G \to G$が定まっていて、さらにある元$e \in G$が指定されていて、
(1) 任意の$f,g,h \in G$に対して $(f*g)*h=f*(g*h)$
(2) 任意の$g\in G$に対して $g * e = e * g = g$
(3) 任意の$g \in G$に対してある$h\in G$が存在して$g*h=h*g=e$
を満たすとき、$G$は群であるという。$e$を$G$の単位元と言う。(3)における$h$を$g$の逆元と言い、$g^{-1}$で表す。
群$G$が、さらに
(4) 任意の$f,g\in G$に対して$f*g=g*f$
を満たすとき、$G$は可換群またはアーベル群であるという。
$G$が有限集合かつ群であるとき、$G$は有限群であるという。有限群$G$の要素の個数を$G$の位数という。
最低限把握しておいて欲しいのは、
・群というのはある種の集合であること
・群の中でも特別な性質を持つアーベル群というものがあること
・要素の個数を位数と呼ぶこと
ぐらいですかね。より深く理解したい方は、頑張って読み取ってください。演算を表す記号$*$は、以降は省略します。
まず、前節で得られた6つの操作からなる集合
$$ \{ 1, x, x^2, y,xy,x^2y \}$$
は群をなします。これはもう認めてしまうことにします。この群を$X$とおきます。6つの操作は相異なるので、$X$は位数6の有限群です。
$X$の元はすべて、$x$と$y$を何個かかけたものになっています($1$は0個かけたものと見なします)。このようなとき、$X$は$x$と$y$で生成されると言います。また、$\{ x,y \}$は$X$の生成系であると言います。
もう少し厳密に(クリックorタップして展開)
一般に、群$G$の部分集合$S$があって、任意の$g \in G$が
$$ g=h_1h_2\cdots h_n \quad (\text{各 $h_i$ は $S$ の元もしくは $S$ の元の逆元})$$
と表せるとき、$G$は$S$で生成されるという。またこのとき、$S$は$G$の生成系であるという。
前節で、$xy=yx$であることを見ました。このことから、$X$がアーベル群であることが従います。一般に、以下が成り立つことが知られています。
群$G$が部分集合$S$で生成されるとし、$S$の任意の2元$f,g$が可換である、すなわち$fg=gf$を満たすとする。このとき$G$はアーベル群である。
まとめると、
$X$は位数6のアーベル群である。
となります。
$X$の構造
$X$が位数6のアーベル群であることが分かりました。このことから、さらにある事実が導かれます。
有限群はどのような構造を持つか?という問は、古くから多くの数学者達が取り組んでおり、特に位数の小さい群に関してはかなり詳しい結果が知られています。例えばMathpediaの
有限群の分類(位数1~100)
を参照。
我々が着目している群$X$は、位数6の群です。位数6の群がどのような構造を持つかを見てみると、実はたったの2パターンしかないということが分かります。上のリンクにも証明がありますが、tsujimotter 氏の
位数6の群の分類
にも詳細な解説があります。
2つのパターンというのは、「6次巡回群$C_6$」と、「3次対称群$S_3$」です。$S_3$についての説明は省略します。$C_6$は、
$$ C_6=\{ 1, g, g^2, g^3, g^4, g^5 \}$$
という形の群です。ただし、$g$は6乗して初めて$1$になるような元です。$C_6$は1つの元で生成されることが分かります。
$X$は$C_6$か$S_3$のどちらかと同じ構造を持ちますが、さらに$C_6$はアーベル群であり、$S_3$はアーベル群でないことが知られています。$X$はアーベル群だったので、$X$は$C_6$と同じ構造であることが分かります!このとき、$X$は$C_6$と同型であると言います。
より厳密に(クリックorタップして展開)
2つの群$G_1,G_2$が同型であるとは、2つの写像$f_1: G_1 \to G_2, f_2 : G_2 \to G_1$があって、
(1) 任意の$g,h \in G_1$ に対して$f_1(gh)=f_1(g)f_1(h)$
(2) 任意の$g',h' \in G_2$ に対して$f_2(g'h')=f_2(g')f_2(h')$
(3) $f_2 \circ f_1 = \mathrm{id}_{G_1}$
(4) $f_1 \circ f_2 = \mathrm{id}_{G_2}$
を満たすことを言います。ちなみに、(2)は(1)(3)(4)から導かれるので、省略できます。
前節で$X$は$x$と$y$で生成されると述べましたが、$C_6$と同型であるということは、実は1つの元で生成されるということになります。このことを念頭に置いて調べてみると、
\begin{eqnarray}
(xy)^0&=&1\\
(xy)^1&=&xy\\
(xy)^2&=&x^2y^2=x^2\\
(xy)^3&=&x^3y^3=y\\
(xy)^4&=&x^4y^4=x\\
(xy)^5&=&x^5y^5=x^2y\\
\end{eqnarray}
より、$X$は$xy$で生成されることが分かります。
ここまで長々と書いてきましたが、この「$X$は$xy$で生成される」というのが最終的に言いたかったことです。これを用いて、冒頭の問題の別解が得られます。
OMC206(E)別解
$x,x^{-1},y$を定義するところまでは公式解説と同じとする。さらに、$x$の後に$y$を行う操作を$z$とおく。つまり$z$は
$z: A \longrightarrow E \longrightarrow C \longrightarrow D \longrightarrow B \longrightarrow F \longrightarrow A$
という操作である。次のことが確かめられる。
- $z$を2回行うことは$x^{-1}$と同じ
- $z$を3回行うことは$y$と同じ
- $z$を4回行うことは$x$と同じ
- どの色の組から初めても、$z$を6回行うと初めて元に戻る
したがって、ある色の組から始めて$x,x^{-1},y$を$n$回行って元に戻る操作の個数は、$f(z)=(z^2+z^3+z^4)^n$の次数が6の倍数である項の係数和に等しい。あとは、$1$の6乗根を用いて公式解説と同様にすればよい。以下略。
いかがでしょうか。$X$が1つの元で生成されるということから、2変数多項式の代わりに1変数多項式を使うことができる、ということに繋がりました。
これが良い解き方だと言うつもりは全くありません。公式解説より手間が減るわけでもありませんし。あくまで、群論の知識があればこのような見方も可能、ということを紹介することがこの記事の目的です。
それでは。