OMC204 参加記

こんばんは。simasimaです。
本記事では 2024/1/31 に開催された OMC204 の感想などを書いていきます。
今回から全ての参加記に注意書きを付ける事にしました。この注意書きがあったからといってセットが駄目だったという訳ではないので安心してください。
また、今回から評価基準を新しくしました。詳しくは評価の章を見てください

A

A
漸化式を解こうと色々変数をずらしていたが、実験すればすぐ解けた。
ただ計算するのが一番速いというのはちょっと問題としてどうかという気もするのだが、性質自体は綺麗で、200点のA問題と考えると十分許容範囲と言えるだろう。ここで方針を誤ってもロスする時間は少ないし、4eなら巻き返すポイントが幾らでもある。
所要時間：5分

B

B
今回の大やらかしポイント。角度と相似が見えず時間を使ってしまった。さらに相似が見えた後も計算ミスで答えが有理数にならず苦労した。さらにタイピングミスでペナも追加。この時点でスピード勝負であるを考えると今回の優勝は厳しい事を悟る。しかし、この問題は上位勢でも意外と時間を掛けている人も多かったので後から見れば意外と滅茶苦茶悪い結果では無かったのかもしれない。
この問題は300点にしては難しい方だが、解答を見れば300点でもいいかなという気もする。相似と角度追跡だけで解けてそこそこ難しい問題を作れるのは評価に値する。
所要時間：23分＋1ペナ

C

C
かなりビハインドを背負ってしまったがここから幾何が無いので、優勝を狙ってここから攻めを意識し始める。
最初は展開図もどきを書いて算数パズルで処理しようと思ったが、かなり無理そう。正射影の話を思い出してなんとか軌道修正した。
微妙に算数で解けそうな設定になっているのがこの問題のいやらしい所で、図を書いて面積の議論をし始めた時点でこの問題の罠に既に嵌っているのだ。この発想の問題は一回見たことがあったが、OMCでは初めて出たと思う。一回も見たことが無かったらこの解法で解けなかったと思う。ただ、知らなくても算数パズルと辺計算で頑張れば処理出来るらしいので一応救済にもなっている。解説の解法で解くのが難しい所が少し残念だが、問題だけ見れば4eのこの位置の問題としてはほぼ完璧な出来だと思う。
所要時間：10分

D

D
問題の設定が綺麗なタイプの問題。初手で全ての項に$d_{30}$を掛けた。$d_{15}$と$d_{30}$を$d_{n}$と$d_{2n}$に置き換えて考察していたが、約数の個数が$30$個である事が強い条件だったので、そこから絞った方が若干処理が速かった気がするのでそこが反省点。計算ミスで1ペナ
最初に $d_{30}$ を掛けて$d_{15}$の約数の条件を見つけるのが考察の本質だった。　その後の考察は場合分けすれば何とかなる感じで、処理がちょっと重めな問題だった。$d_7,d_8$の条件が問題の本質とあんまり関係ないのに処理が重かったので、もうちょっといい感じの条件が無かったのかとちょっと思った。
所要時間：13分+1ペナ

E

E
問題を頑張って読んでちょっとずつ整理するともう答えだったという感じ。何も考察していない。累積和をとる所が恐らくこの問題で難しい部分だが、競プロをやっている人にはこのパートは簡単だったと思う。例えば同じような発想をする似たような競プロの問題として AGC023-A Zero-Sum Ranges が挙げられるがこれは緑Diff(しかも5年前)である。競プロをやっていないとこれは気づかないので、仕方ないと言えば仕方ないのかもしれない。計算パートでは適当にやっていると電卓の上限を超えるので非本質的な工夫を強いられる。私は21!/(7!7!7!)を計算してその数との比で何とか処理した。想定解と異なる解法の計算をきつくしようとして数値を大きくしたいのは分かるが、公式の電卓より外部の電卓の方が有利になる数値設定はやめて欲しい。電卓の有効数字がもっと多ければいいんだけどね...
4bのFに置かれた400点問題として見れば面白い問題だと思う。
所要時間：8分

F

F
5完した時点で順位表を見ると、FはまだFAは出ておらず、1位だった(ペナ消費後は2位)ので取りあえず負けは無くなって一安心。このままFが誰も解けない展開なら優勝だがEの難易度と同じと考えるとFもある程度簡単であることが想定されるので、このFを取らないと優勝はないだろう。愚直に$x^n$を$Q(x)$で割ると二項係数が出て来て、$x$の係数と定数がどちらも$0$であることから多項式をいろいろ互除したが、結局複素数ではなく実数の組を数えなければいけなかったのでそこが解決できなかった。解説を見ると最初の変形から間違っていた。そこさえ越えられれば場合分けで解ける問題だったので、解くのは不可能では無かったと思う。時間的に勝っているのだから焦らず最初の方針決めに時間を割けば良かったと反省。
所要時間：-

最終結果

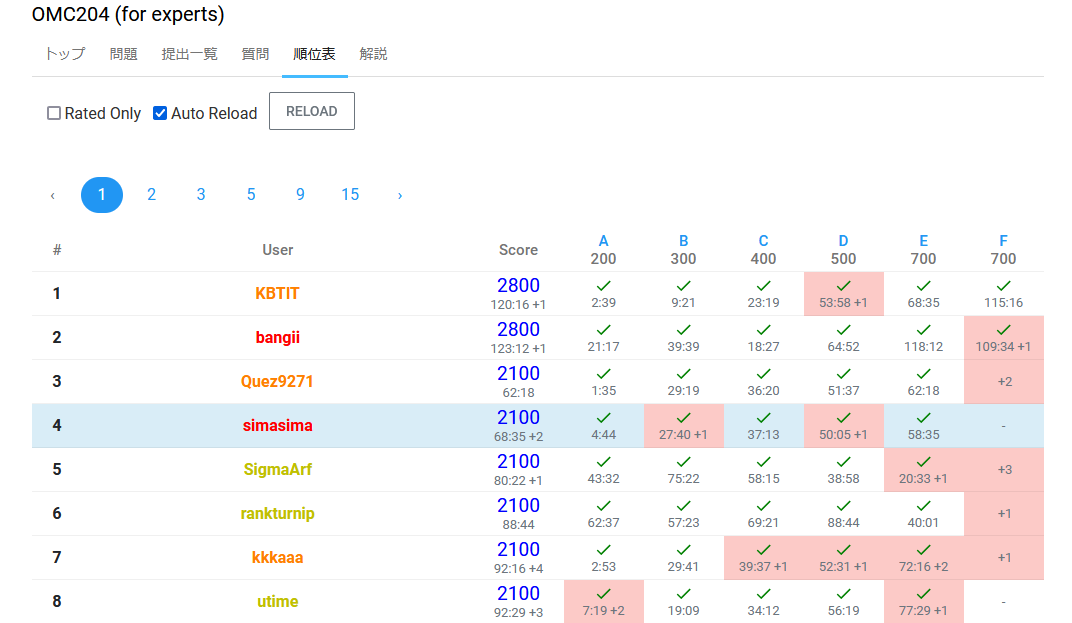順位表
全完2人とペナ差で1人に抜かれて4位だった。Bでの出遅れをCDEで見事にひっくり返したところまでは良かったが、Fで焦って解けなかったのは反省。F幾何なんかよりは全然優勝の可能性があったのでかなり悔しい。

評価

色々あって、今回から評価の制度を変えた。
○　★に満たなかった問題。半数以上の問題がここに入ると思う。
★　総合的に見て特に評価に値すると感じた問題
★★　★以上の中でも上位50％に入る良問
★★★　★★以上の中でも上位50％に入る良問
★★★★　★★★以上の中でも上位50％に入る良問
...
今回の問題の評価
○,★,★★,○,○,★★

今回のセットは特に良問と感じる問題が多かったので★を3問に付けたが、★の評価はかなり厳しいので★が付いていない問題が悪問という訳ではないという事に留意して欲しい。★が1問もつかないセットも今後沢山出て来ると思う。