2016 Canada MO P5を解く(+自己紹介?)
本記事では，三角形$XYZ$の外接円を円$XYZ$と表すことがある．
自己紹介?
こんにちは，Melidです．幾何学が好きです．気まぐれで記事を投稿していこうと思います．
本題
さて，今回は以下の問題を解いていきます．
鋭角三角形$ABC$において，$A,B$から$BC,CA$に下ろした垂線の足をそれぞれ$D,E$とし，$AD$と$BE$の交点を$H$とする．線分$AB$の中点を$M$とし，三角形$DEM$の外接円と三角形$ABH$の外接円の$2$つの交点を$P,Q$($P$は$CH$に関して$A$と同じ側にある)とする．このとき，$3$つの直線$ED,PH,MQ$は三角形$ABC$の外接円上の$1$点で交わることを示せ．
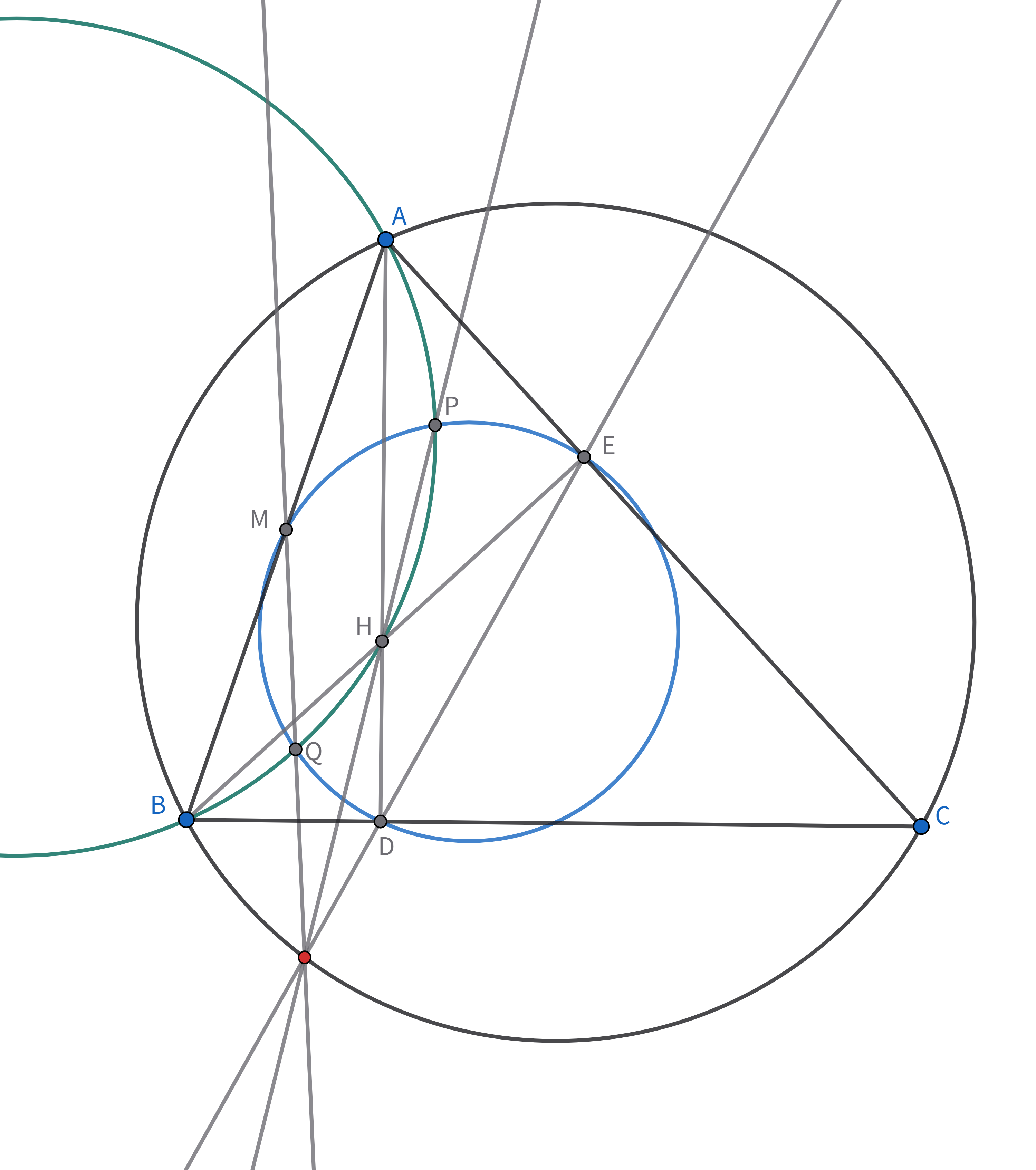
解説
とりあえず$AB$を直径とする円で反転してみましょう．
$M$に関して$H$と対称な点は円$ABC$上にあることが知られているので，$H$は円$ABC$上の点に移ります．つまり，円$ABH$と円$ABC$は互いに入れ替わります．
さらに，円$DEM$と直線$DE$も互いに入れ替わることが分かります．
よって，$Q$は円$ABC$と半直線$ED$の交点に移るので，$ED$と$MQ$は円$ABC$上で交わることが示せました．
今度は中心$H$，半径$ \sqrt{HA \times HD}i $の円で反転してみましょう．
円$ABH$と直線$DE$が互いに入れ替わり，円$DEM$と円$ABC$が互いに入れ替わります．
よって，$P$も円$ABC$と半直線$ED$の交点に移るので，$PH$と$ED$は円$ABC$上で交わることが示せます．
前の議論と併せて，命題が示せました．
練習問題
上記の構図で成り立つ他の性質です．気が向いたら解いてみてください．
$CP=CQ$を示せ．
$CH$と$AB$の交点を$F$とする．このとき，円$ABD$，円$CFM$，中心が$C$で半径が$CP$の円は共軸であることを示せ．
終わりに
記事を書くのは初めてなので拙い点もあるかと思いますが，温かい目で見ていただければ幸いです．
この記事を高評価した人
この記事に送られたバッジ
投稿者
