Diaryの積分を解いてみた1
Diary?
時折簡単ですが、基本かなり難しい(まじでむずい)問題を出してくれるbotです。 こちら がそのアカウント。
$$\int \sqrt\frac{x+\sqrt{x^2+1}}{x+\sqrt{x^2-1}}dx$$
いかつ。解きます。
準備
$$\int \sqrt{x^2+ax+b}\ dx=\frac{1}{2}\left(b-\frac{a^2}{4}\right)\left(x\sqrt{x^2+1}+\ln(x+\frac{a}{2}+\sqrt{x^2+ax+b})\right)+C''$$
$\displaystyle J=\int \sqrt{x^2+ax+b}\ dx$ とする。
$$J=\int \sqrt{\left(x+\frac{a}{2}\right)^2+\left(b-\frac{a^2}{4}\right)}\ dx$$
$\displaystyle x+\frac{a}{2}=\sqrt{b-\frac{a^2}{4}}\sinh{θ}$ とおくと、$\displaystyle dx=\sqrt{b-\frac{a^2}{4}}\cosh{θ}dθ$
$$\therefore J=\int \sqrt{\left(b-\frac{a^2}{4}\right)(\sinh^2{θ}+1)}\sqrt{b-\frac{a^2}{4}}\cosh{θ}dθ=\left(b-\frac{a^2}{4}\right)\int \cosh^2{θ}dθ$$
$$=\frac{1}{2}\left(b-\frac{a^2}{4}\right)(θ+\sinh{θ}\cosh{θ})+C'$$
ここで、
$$θ=\mathrm{arsinh}\frac{x+\frac{a}{2}}{\sqrt{b-\frac{a^2}{4}}}=\ln(x+\frac{a}{2}+\sqrt{x^2+ax+b})-\frac{1}{2}\ln(b-\frac{a^2}{4})\ ,$$
$$\cosh{θ}=\sqrt{\sinh^2{θ}+1}=\sqrt{x^2+1}$$
$$\therefore J=\frac{1}{2}\left(b-\frac{a^2}{4}\right)\left(x\sqrt{x^2+1}+\ln(x+\frac{a}{2}+\sqrt{x^2+ax+b})\right)+C''$$
解説
$$I=\int \sqrt\frac{x+\sqrt{x^2+1}}{x+\sqrt{x^2-1}}dx$$
$$\sqrt{2x+2\sqrt{x^2+1}}=\sqrt{x-i}+\sqrt{x+i}\ ,\ \sqrt{2x+2\sqrt{x^2-1}}=\sqrt{x-1}+\sqrt{x+1}$$
$$\therefore I=\int\frac{\sqrt{x-i}+\sqrt{x+i}}{\sqrt{x-1}+\sqrt{x+1}}dx=\int\frac{(\sqrt{x-i}+\sqrt{x+i})(\sqrt{x-1}-\sqrt{x+1})}{(\sqrt{x-1}+\sqrt{x+1})(\sqrt{x-1}-\sqrt{x+1})}dx$$
$$=\int\frac{\sqrt{x^2-(1+i)x+i}+\sqrt{x^2-(1-i)x-i}-\sqrt{x^2+(1-i)x-i}-\sqrt{x^2+(1+i)+i}}{-2}dx$$
補題1より、
$$\int \sqrt{x^2-(1+i)x+i}\ dx=\frac{1}{2}\left(i-\frac{(1+i)^2}{4}\right)\left(x\sqrt{x^2+1}+\ln(x-\frac{1+i}{2}+\sqrt{x^2-(1+i)x+i})\right)+C_1$$
$$=\frac{i}{4}\left(x\sqrt{x^2+1}+\ln\left(x-\frac{1+i}{2}+\sqrt{x-1}\sqrt{x-i}\right)\right)+C_1$$
$$\int \sqrt{x^2-(1-i)x-i}\ dx=\frac{1}{2}\left(-i-\frac{(1-i)^2}{4}\right)\left(x\sqrt{x^2+1}+\ln(x-\frac{1-i}{2}+\sqrt{x^2-(1-i)x-i})\right)+C_2$$
$$=-\frac{i}{4}\left(x\sqrt{x^2+1}+\ln\left(x-\frac{1-i}{2}+\sqrt{x-1}\sqrt{x+i}\right)\right)+C_2$$
$$\int \sqrt{x^2+(1-i)x-i}\ dx=\frac{1}{2}\left(-i-\frac{(1-i)^2}{4}\right)\left(x\sqrt{x^2+1}+\ln(x+\frac{1-i}{2}+\sqrt{x^2+(1-i)x-i})\right)+C_3$$
$$=-\frac{i}{4}\left(x\sqrt{x^2+1}+\ln\left(x+\frac{1-i}{2}+\sqrt{x+1}\sqrt{x-i}\right)\right)+C_3$$
$$\int \sqrt{x^2+(1+i)x+i}\ dx=\frac{1}{2}\left(i-\frac{(1+i)^2}{4}\right)\left(x\sqrt{x^2+1}+\ln(x+\frac{1+i}{2}+\sqrt{x^2+(1+i)x+i})\right)+C_4$$
$$=\frac{i}{4}\left(x\sqrt{x^2+1}+\ln\left(x+\frac{1+i}{2}+\sqrt{x+1}\sqrt{x+i}\right)\right)+C_4$$
$$\therefore -2I=\frac{i}{4}\ln\left(x-\frac{1+i}{2}+\sqrt{x-1}\sqrt{x-i}\right)-\frac{i}{4}\ln\left(x-\frac{1-i}{2}+\sqrt{x-1}\sqrt{x+i}\right)+\frac{i}{4}\ln\left(x+\frac{1-i}{2}+\sqrt{x+1}\sqrt{x-i}\right)-\frac{i}{4}\ln\left(x+\frac{1+i}{2}+\sqrt{x+1}\sqrt{x+i}\right)+C$$
長いが整理すると、
$$I=\frac{i}{8}\ln\frac{(2x+1+i+2\sqrt{x+1}\sqrt{x+i})(2x-1+i+2\sqrt{x-1}\sqrt{x+i})}{(2x+1-i+2\sqrt{x+1}\sqrt{x-i})(2x-1-i+2\sqrt{x-1}\sqrt{x-i})}+C$$
オフチョベットしたテフをマブガッドしてリットにしたような式になってしまいました。
conclusion
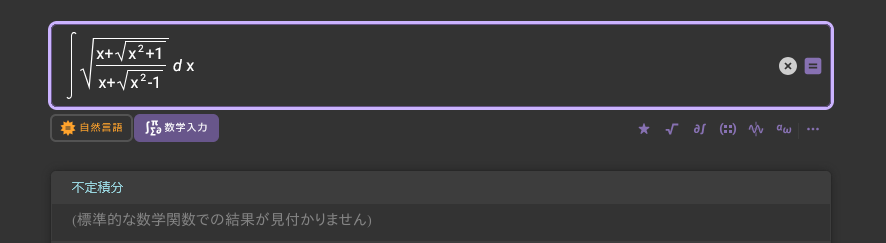インジェラ積分(?)
こういうことですので。最終形などなんでもいいのです...。以上...。
