電卓のみで実践できるちょっと自慢できる数学

こんにちは、名誉毀損です.
ちょっとキャッチーなテーマをやってみたいなと考えて、今回は電卓ですぐに確かめられるちょっとした豆知識を紹介しようと思います.

やり方

まず、電卓を用意します。やり方は簡単で
最初は２を入力し、それにルートをつけます.
次に２を足し、またルートをつけます.
次に２を足し、またルートをつけます.
次に２を足し、またルートをつけます.
・・・
これを無限回繰り返すとどうなったでしょう.
実際にやってもらうと２になることが分かります.
$2= \sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2 \cdots }}}} $
一見、不思議に見えますね.この２を３に変えてみるとどうでしょう.
これも実際にやってもらうと３にはならず
ぐちゃぐちゃな数字になってしまいますね.
次にきれいな数になるのは６のときになります.
この現象の背景を見てみることにしましょう.

理論的な背景

さて、前述でやったことはどう数学語で書けるでしょうか.
それは次のようになります.

$$ \begin{eqnarray} \left\{ \begin{array}{l} a_1=m \\ a_{n+1}=\sqrt{a_n+m} \end{array} \right. \end{eqnarray} $$
を満たす数列$\{a_n\}$を考えるとき、$\lim_{n \to \infty}a_n$はどうなるだろうか.

これは次のようなグラフを考えると答えが求められます.

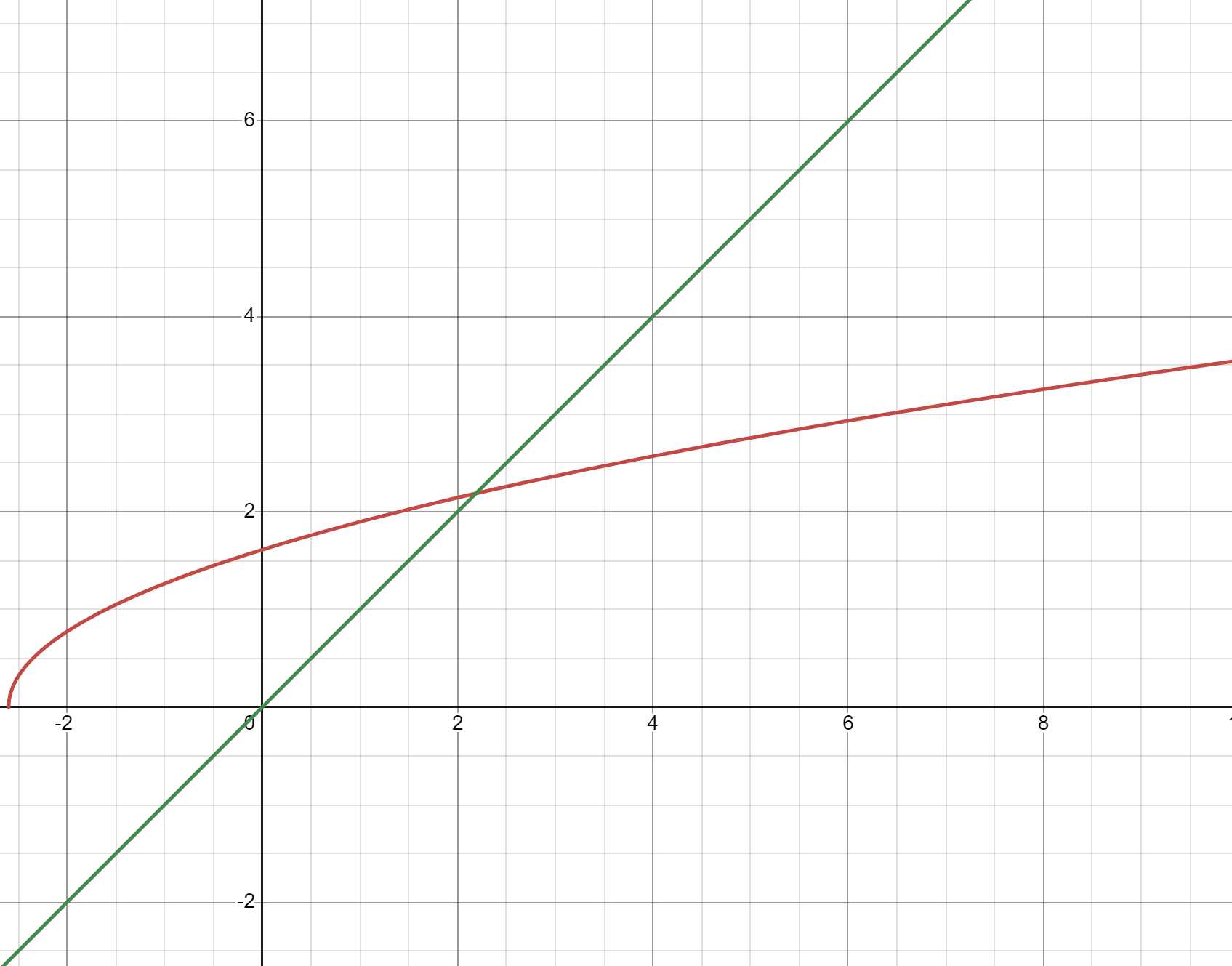
緑は$y=x$,赤は$f(x)=y=\sqrt{x+m}$です.
与えられた漸化式は$a_{n+1}=f(a_n)$に書き換えられます.
この交点は$x=\frac{1+\sqrt{4m+1}}{2}$であり、$m<\frac{1+\sqrt{4m+1}}{2}$となっているため,高校数学定番の解法を用いることによって
即座に$\lim_{n \to \infty}a_n=\frac{1+\sqrt{4m+1}}{2}$を得られます.
つまり、$\sqrt{4m+1}$が奇数になれば計算結果がきれいな数になります.
$\sqrt{4m+1}=2k+1$
$ \Longleftrightarrow 4m+1=4k^2+4k+1$
$\Longleftrightarrow m=k(k+1) $
よって、$m$は連続する２整数であればよいことが分かりました.