曲線の面積を求める
Osgood曲線というものの面積を求めます。
Osgood曲線とは?
Osgood curveのwikipedia の Definition and propertiesにはこう書かれています。
A curve in the Euclidean plane is defined to be an Osgood curve when it is non-self-intersecting (that is, it is either a Jordan curve or a Jordan arc) and it has positive area.[1] More formally, it must have positive two-dimensional Lebesgue measure.
日本語にするとこんな感じ
ユークリッド平面内の曲線がOsgood曲線であるとは、その曲線が自己交差しない(つまり、それがJordan曲線またはJordan弧である)かつ、正の面積を持つときに言います。より正式には、その曲線は正の2次元ルベーグ測度を持つ必要があります。
ということ。つまりは、「自己交差せずに正の二次元ルベーグ測度を持つ連続な曲線」なら何でもOsgood曲線と言ってもいいということなんですね。
なのでめちゃくちゃたくさんの種類があります。
よって面積は一意に定まりません。
画像の面積を求める
Osgood曲線の面積を求めるわけではなくて、画像の曲線の面積と、[0,1]からℝ²への関数としての表示を求めてくださいと言われたのでした。
画像はこれです。
一度mathlogに画像をアップロードして内部htmlからリンクを取得すれば、imgタグのsrcに入れると 図1 とかの文字なしの画像を埋め込めますね。
そして Osgood curveのwikipedia にある画像がこちら

By David Eppstein - Own work, CC0, Link
完全にこの画像ですね。
この画像の説明にはこう書かれています。
Example of an Osgood curve, constructed by recursively removing wedges from triangles. The wedge angles shrink exponentially, as does the fraction of area removed in each level, leaving nonzero area in the final curve.
訳すとこう
Osgood曲線の一例。これは、三角形からくさび形の部分を再帰的に取り除くことで構成される。このとき、くさびの角度は指数関数的に小さくなり、各段階で取り除かれる面積の割合も指数的に減少する。その結果、最終的に残る曲線は非ゼロの面積を持つ。
確かに、奥のほうは角度が狭くなっていますね。
...
指数関数的な減少なので、こういう風に定義するとどうでしょうか
\begin{eqnarray} \theta_n = \theta e^{an} \quad (a<0) \end{eqnarray}
$\theta_n$はくさび型の三角形の一番小さい角度(頂角と呼ぶことにする)とします。
あとは、最初の三角形の形を設定すればいいですね。
底辺は$1$、高さは$b$としましょうか。
気持ち的にはこうです
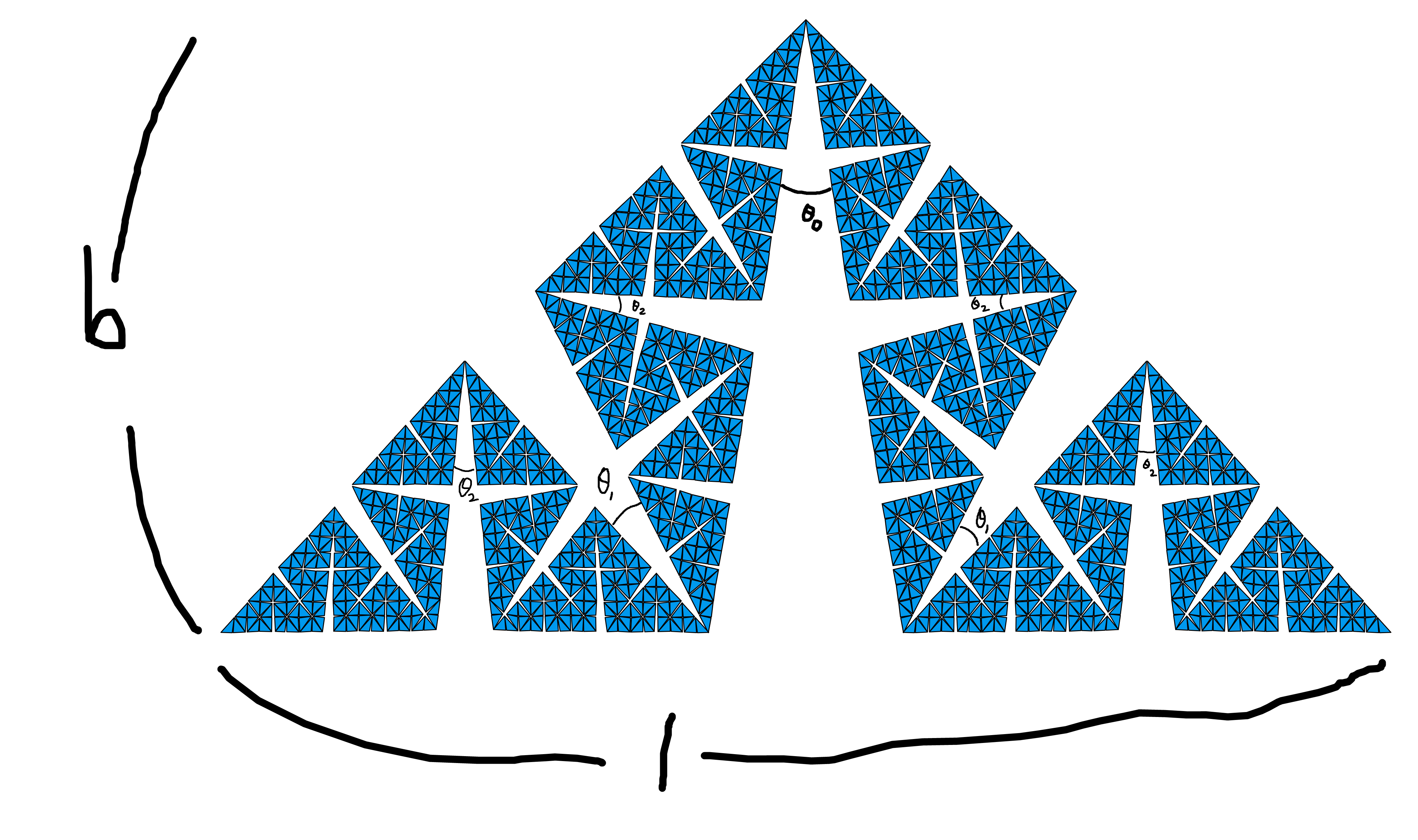
なるほどね
ここで気づいたのですが、最初の三角形以外青い三角形は二等辺三角形とは言えないんですね。
なので取り除くくさびはくさびの頂角の二等分線が青い三角形の対辺の中点を通るようにします。
値を求める

青い部分の面積が欲しいです
$CD=m$とします。中線定理より、
\begin{eqnarray}
a^2+b^2&=&2(AD^2+m^2) \\
a^2+b^2&=&2AD^2+2m^2 \\
\frac12(a^2+b^2)-AD^2&=&m^2 \\
\frac12(a^2+b^2)-\frac{c^2}4 &=& m^2 \\
\frac12\sqrt{2a^2+2b^2-c^2} &=& m
\end{eqnarray}
$\psi = \angle ABC$$\phi=\angle BDC$とします。$\triangle BDC$の辺$BD$の高さや辺$DB$の長さを考えると
\begin{eqnarray}
m\sin(\phi) &=& a\sin(\psi) \\
m\cos(\phi) &=& \frac c2- a\cos(\psi)
\end{eqnarray}
と分かるので、
\begin{eqnarray}
\sin(\phi) &=& \frac am\sin(\psi) \\
\cos(\phi) &=& \frac c{2m}-\frac am\cos(\psi)
\end{eqnarray}
となります。
ここで$\phi+\frac \theta2$の$\sin$と$\cos$を求めます
\begin{eqnarray}
\sin(\phi+\frac \theta2) &=& \sin(\phi)\cos(\frac \theta2)+\cos(\phi)\sin(\frac \theta2)
\\&=&\frac am\sin(\psi)\cos(\frac \theta2)+\qty(\frac c{2m}-\frac am\cos(\psi))\sin(\frac\theta2)
\\&=&\frac am\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+\frac c{2m}\sin(\frac\theta2)
\\\\
\cos(\phi+\frac\theta2)&=&\cos(\phi)\cos(\frac\theta2)-\sin(\phi)\sin(\frac\theta2)
\\&=&\qty(\frac c{2m}-\frac am\cos(\psi))\cos(\frac\theta2)-\frac am\sin(\psi)\sin(\frac\theta2)
\\&=&-\frac am\qty(\cos(\psi)\cos(\frac\theta2)+\sin(\psi)\sin(\frac\theta2))+\frac c{2m}\cos(\frac\theta2)
\end{eqnarray}
ここで辺$CF$を底辺とみて$\triangle CDF$の高さを考えることで、
\begin{eqnarray}
m\sin(\frac\theta2) &=& DF\sin(\frac\theta2+\phi) \\
DF &=& \frac{\sin(\frac\theta2)}{\sin(\frac\theta2+\phi)}m
\\&=& \frac{\sin(\frac\theta2)}{\frac am\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+\frac c{2m}\sin(\frac\theta2)}m
\\&=& \frac{\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)}m^2
\end{eqnarray}
と求まります。
もう一個の$DE$は$a$と$b$を入れ替えればいいので
\begin{eqnarray}
DE &=& \frac{\sin(\frac\theta2)}{b\qty(\sin(\psi')\cos(\frac\theta2)-\cos(\psi')\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)}m^2
\end{eqnarray}
ここで$\psi' = \angle BAC$です。
(これ$\psi'$は$\psi$に統一しといたほうがいいよな...)
と思ったので
\begin{eqnarray}
b\sin(\psi') &=& a\sin(\psi) \\
b\cos(\psi') &=& c -a\cos(\psi)
\\\\
\sin(\psi') &=& \frac ab\sin(\psi) \\
\cos(\psi') &=& \frac cb -\frac ab\cos(\psi)
\end{eqnarray}
ということなので
\begin{eqnarray}
DE &=& \frac{\sin(\frac\theta2)}{b\qty(\sin(\psi')\cos(\frac\theta2)-\cos(\psi')\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)}m^2
\\&=& \frac{\sin(\frac\theta2)}{b\qty(\frac ab\sin(\psi)\cos(\frac\theta2)-\frac c{b}\sin(\frac\theta2)+\frac ab\cos(\psi)\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)}m^2
\\&=&\frac{\sin(\frac\theta2)}{\qty(a\sin(\psi)\cos(\frac\theta2)-c\sin(\frac\theta2) +a\cos(\psi)\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)}m^2
\\&=&\frac{\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2) +\cos(\psi)\sin(\frac\theta2))-\frac c{2}\sin(\frac\theta2)}m^2
\end{eqnarray}
似てますね
右の三角形の面積は、
\begin{eqnarray}
&&\frac S2- \frac {2DF}c \frac S2
\\&=&\frac S2- \frac {DF}c S
\\&=&\frac S2- \frac Sc\frac{\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2) -\cos(\psi)\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)}m^2
\\&=&\frac S2- S\frac{m^2\sin(\frac\theta2)}{ac\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+\frac {c^2}{2}\sin(\frac\theta2)}
\\&=&\frac S2- S\frac{4m^2\sin(\frac\theta2)}{4ac\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+2c^2\sin(\frac\theta2)}
\end{eqnarray}
左は、
\begin{eqnarray}
&&\frac S2- \frac {2DE}c \frac S2
\\&=&\frac S2- \frac {DE}c S
\\&=&\frac S2- \frac Sc\frac{\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2) +\cos(\psi)\sin(\frac\theta2))-\frac c{2}\sin(\frac\theta2)}m^2
\\&=&\frac S2- S\frac{m^2\sin(\frac\theta2)}{ac\qty(\sin(\psi)\cos(\frac\theta2)+\cos(\psi)\sin(\frac\theta2))-\frac {c^2}{2}\sin(\frac\theta2)}
\\&=&\frac S2- S\frac{4m^2\sin(\frac\theta2)}{4ac\qty(\sin(\psi)\cos(\frac\theta2)+\cos(\psi)\sin(\frac\theta2))-2c^2\sin(\frac\theta2)}
\end{eqnarray}
一応面積が出ましたが、再帰するには小さい三角形に対応する$a,b,c,\psi$が必要です
 再掲
再掲
で、必要なのは左の三角形に対する$\sin(\psi_1),\cos(\psi_1),a_1,b_1,c_1$と
右の三角形に対する$\sin(\psi_2),\cos(\psi_2),a_2,b_2,c_2$です。
右の方は
\begin{eqnarray}
\sin(\psi_1)=\sin(\angle FBC),\cos(\psi_2)=\cos(\angle FBC),c_1=BC,a_1=BF,b_1=FC
\end{eqnarray}
左は
\begin{eqnarray}
\sin(\psi_2)=\sin(\angle EAC),\cos(\psi_2)=\cos(\angle EAC),c_2=AC,a_2=AE,b_2=EC
\end{eqnarray}
です。
右から行きましょうか
\begin{eqnarray}
\sin(\angle FBC) &=& \sin(\psi) \\
\cos(\angle FBC) &=& \cos(\psi) \\
c_1 &=& a \\
a_1 &=& \frac c2-DF
\\&=&\frac c2-\frac{\sin(\frac\theta2)}{\sin(\frac\theta2+\phi)}m
\\&=&\frac c2-\frac{\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)}m^2
\\b_1 &=& CF
\end{eqnarray}
ここで$CF$ですが、$\triangle BCF$の高さを考えることで、
\begin{eqnarray}
CF\sin(\frac\theta2+\phi) &=& a\sin(\psi) \\
CF &=& \frac{\sin(\psi)}{\sin(\frac\theta2+\phi)}a \\
&=&\frac{am\sin(\psi)}{a\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)} \\
\end{eqnarray}
となります。再帰できます。
左の方は
\begin{eqnarray}
b\sin(\angle EAC) &=& a\sin(\psi) \\
\sin(\angle EAC) &=& \frac ab\sin(\psi)\\
b\cos(\angle EAC) &=&c- a\cos(\psi) \\
\cos(\angle EAC) &=& \frac cb-\frac ab\cos(\psi)\\
c_2 &=& b \\
a_2 &=& \frac c2-DE
\\&=&\frac c2-\frac{m^2\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2) +\cos(\psi)\sin(\frac\theta2))-\frac c{2}\sin(\frac\theta2)}
\\b_2 &=& CE
\end{eqnarray}
ここで$CE$ですが、$\triangle CEB$の高さを考えることで、
\begin{eqnarray}
CE\sin(-\frac\theta2+\phi) &=& a\sin(\psi) \\
CE &=& \frac{\sin(\psi)}{\sin(-\frac\theta2+\phi)}a \\
\\&=&\frac{am\sin(\psi)}{a\qty(\sin(\psi)\cos(\frac\theta2) +\cos(\psi)\sin(\frac\theta2))-\frac c{2}\sin(\frac\theta2)}
\end{eqnarray}
これで再帰が完全にできますね!
\begin{eqnarray}
m &=& \frac12\sqrt{2a^2+2b^2-c^2}
\end{eqnarray}
右
\begin{eqnarray}
S_r&=&\frac S2- S\frac{4m^2\sin(\frac\theta2)}{4ac\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+2c^2\sin(\frac\theta2)}
\\
\sin(\angle FBC) &=& \sin(\psi)
\\
\cos(\angle FBC) &=& \cos(\psi)
\\
c_1 &=& a
\\
a_1 &=&\frac c2-\frac{\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)}m^2
\\b_1 &=& \frac{am\sin(\psi)}{a\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)} \\
\end{eqnarray}
左
\begin{eqnarray}
S_l&=&\frac S2- S\frac{4m^2\sin(\frac\theta2)}{4ac\qty(\sin(\psi)\cos(\frac\theta2)+\cos(\psi)\sin(\frac\theta2))-2c^2\sin(\frac\theta2)}\\
\sin(\angle EAC) &=& \frac ab\sin(\psi)\\
\cos(\angle EAC) &=& \frac cb-\frac ab\cos(\psi)\\
c_2 &=& b \\
a_2 &=& \frac c2-\frac{m^2\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2) +\cos(\psi)\sin(\frac\theta2))-\frac c{2}\sin(\frac\theta2)}
\\b_2 &=& \frac{am\sin(\psi)}{a\qty(\sin(\psi)\cos(\frac\theta2) +\cos(\psi)\sin(\frac\theta2))-\frac c{2}\sin(\frac\theta2)}
\end{eqnarray}
一応Geogebraで書いていたサイトを保存しておきます。
https://www.geogebra.org/calculator/ekhrw5nf
プログラム
これで一仕事はしました。が、次も大きな仕事があります
プログラミングです。
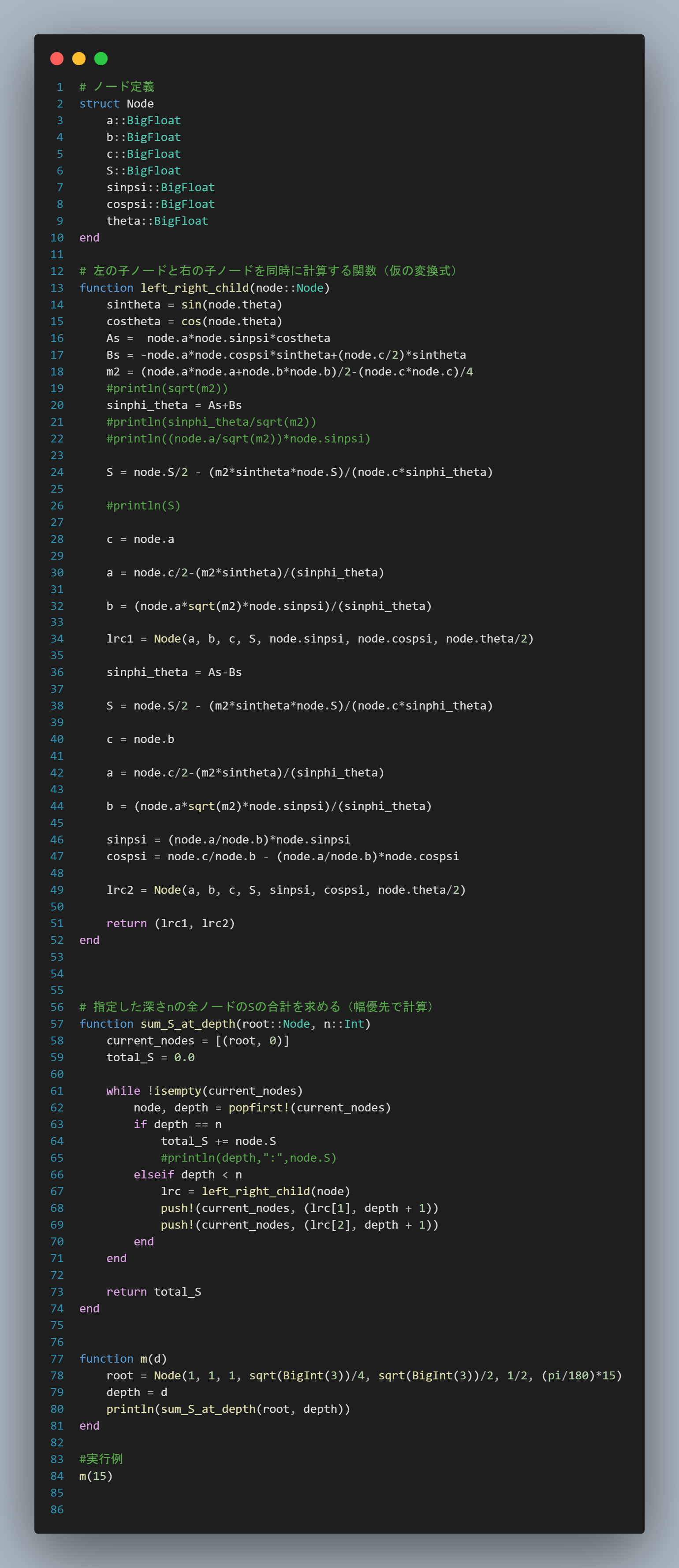 ざっとこんな感じですね。
ざっとこんな感じですね。
$n$回分割していくと三角形の数が$2^n$個になるので頑張っても$23$回分割で、
ぱっと求めるには$20$回分割ぐらいしかできないです
結果
試しに正三角形から初めて$\theta_n=30\degree\cdot2^{-n}$でやりました。
\begin{eqnarray}
S_1&=&0.2320508075688773166051925059656452240866723649140120384651322164958122962272924\\
S_2&=&0.1803675244988207080116317986079005515372398980584778518136842546569495933891843\\
S_3&=&0.1606451381723249784180454293218508497573398011502433311356028613314800011200362\\
S_4&=&0.1495657798725541834417913029772603360518663622406790293239079990976682629898696\\
S_5&=&0.144446433806644429774981083621989609918207657569345706608446486818457547591952\\
S_6&=&0.1417856486784250519311043457431398909101912772506910733312850802566257244276233\\
S_7&=&0.1404830359759840363598149406215973262038884311560136739522018694794239605574951\\
S_8&=&0.1398248686416135048358952007987669297157434819392934443954784015075960523603571\\
S_9&=&0.1394975405346236570452757536502778268355650061096257117693640874810374437428807\\
S_{10}&=&0.1393334390725284647816767670137192849909618333862113074073322582789174466860375\\
S_{11}&=&0.1392514983309392710364239425490532750011338173380931742657321001761999138197561\\
S_{12}&=&0.1392105004865535764817862659847070767135805264682918214464518690138055414890557\\
S_{13}&=&0.1391900084427522275467123933000508196607470979557750498244958938649765271133263\\
S_{14}&=&0.1391797607016276917917383600504124192969334826007596880575748498725357478167391\\
S_{15}&=&0.139174637261027686610631125949441059545463834609543048493345632209880660713084\\
S_{16}&=&0.139172075433242972452398956934843265279751122422067557919615567786770190240881\\
S_{17}&=&0.139170794546224235985555833286955821858953648479632395856782521274816008558424\\
S_{18}&=&0.1391701540959965541093110575100093972008509566265556245347663298658180414517524\\
S_{19}&=&0.1391698338725623297516474545430214228075061114283059920866537821645244915645523\\
S_{20}&=&0.1391696737604253148577043185571695189318978243911994721768108373160164444812696\\
S_{21}&=&0.1391695937044617836859217593254448159989315815107224467403278456559985397593117\\
S_{22}&=&0.139169553676453774053577638759258464184357762927205621269243512793344880440069\\
S_{23}&=&0.1391695336624563302583377476464015856711698900743038042294514659322444317394553\\
\end{eqnarray}
だいたい$0.139169...$という感じです。これ以上は何も言えませんね
他の場合も知りたい場合はその条件をコメントに書いてください。私が計算します。
関数
[0,1]からℝ²への関数としての表示を求めます。
といっても僕には具体的な閉じた表示は求められないので、構成の方法だけでも述べようかと思います。
要は$t\;\;(0\le t\le1)$を使ってこの曲線のパラメータ表示をしてということです。
これには各頂点の座標がいります。
 再再掲
再再掲
各頂点の座標を$\overrightarrow{A},\overrightarrow{B},\overrightarrow{C}$とでも置きましょう。
\begin{eqnarray}
DF&=&\frac{\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)}m^2 \\
DE&=&\frac{\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2) +\cos(\psi)\sin(\frac\theta2))-\frac c{2}\sin(\frac\theta2)}m^2
\end{eqnarray}
なので
\begin{eqnarray}
\overrightarrow{F}&=&\overrightarrow{D}+\overrightarrow{DB}\cdot\frac{2}{c}\frac{\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+\frac c{2}\sin(\frac\theta2)}m^2
\\&=&\frac12\qty(\overrightarrow{A}+\overrightarrow{B})+\frac12\qty(\overrightarrow{B}-\overrightarrow{A})\cdot\frac{2\sin(\frac\theta2)}{ac\qty(\sin(\psi)\cos(\frac\theta2)-\cos(\psi)\sin(\frac\theta2))+\frac {c^2}{2}\sin(\frac\theta2)}m^2
\\
\overrightarrow{E} &=& \overrightarrow{D}+\overrightarrow{DA}\cdot\frac{2}{c}\frac{\sin(\frac\theta2)}{a\qty(\sin(\psi)\cos(\frac\theta2)+\cos(\psi)\sin(\frac\theta2))-\frac c{2}\sin(\frac\theta2)}m^2
\\&=&\frac12\qty(\overrightarrow{A}+\overrightarrow{B})-\frac12\qty(\overrightarrow{B}-\overrightarrow{A})\cdot\frac{2\sin(\frac\theta2)}{ac\qty(\sin(\psi)\cos(\frac\theta2)+\cos(\psi)\sin(\frac\theta2))-\frac {c^2}{2}\sin(\frac\theta2)}m^2
\end{eqnarray}
という風に$\overrightarrow{E},\overrightarrow{F}$を求められます。
あとは、
右
\begin{eqnarray}
\overrightarrow{C_l} &=& \overrightarrow{F} \\
\overrightarrow{A_l} &=& \overrightarrow{C} \\
\overrightarrow{B_l} &=& \overrightarrow{B} \\
\end{eqnarray}
左
\begin{eqnarray}
\overrightarrow{C_r} &=& \overrightarrow{E} \\
\overrightarrow{A_r} &=& \overrightarrow{C} \\
\overrightarrow{B_r} &=& \overrightarrow{A} \\
\end{eqnarray}
という風に再帰してあげると、すべての頂点の座標が分かります。
全ての頂点の座標が分かったら、それらを順番に並べます。
並べ方なのですが、最初の三角形$\overrightarrow{A_1},\overrightarrow{B_1},\overrightarrow{C_1}$の組$(\overrightarrow{A_1},\overrightarrow{B_1},\overrightarrow{C_1})$に数値の組$(0,\frac12,1)$を持たせます。
次の三角形の座標二つを作る際、右の方の組($\overrightarrow{B_1}$を持つ方)にはさっきの数値の組$(0,\frac12,1)$の内、真ん中と右の数を選んで新しい組の左右に$(\frac12,,1)$と書き、真ん中には左右の平均値を入れます。つまり$(\frac12,\frac34,1)$となります。
左の方の組($\overrightarrow{A_1}$を持つ方)にはさっきの数値の組$(0,\frac12,1)$の内、真ん中と左の数を選んで新しい組の左右に$(0,,\frac12)$と書き、真ん中には左右の平均値を入れます$(0,\frac14,\frac12)$
これを再帰します。
ちゃんと書くとこう
元
\begin{eqnarray}
\overrightarrow{A},\overrightarrow{B},\overrightarrow{C},(x,y,z)
\end{eqnarray}
計算して
\begin{eqnarray}
\overrightarrow{E},\overrightarrow{F}
\end{eqnarray}
を求める
右
\begin{eqnarray}
\overrightarrow{C_l} &=& \overrightarrow{F} \\
\overrightarrow{A_l} &=& \overrightarrow{C} \\
\overrightarrow{B_l} &=& \overrightarrow{B} \\
(x_1,y_1,z_1) &=& (y,\frac{y+z}2,z)
\end{eqnarray}
左
\begin{eqnarray}
\overrightarrow{C_r} &=& \overrightarrow{E} \\
\overrightarrow{A_r} &=& \overrightarrow{C} \\
\overrightarrow{B_r} &=& \overrightarrow{A} \\
(x_2,y_2,z_2) &=& (x,\frac{x+y}2,y)
\end{eqnarray}
(辺の長さは面積を求めるときに使ったやつをそのまま使います。)
こうして元の三角形$\overrightarrow{A},\overrightarrow{B},\overrightarrow{C},(x,y,z)$から、
次の三角形の座標を二つ$\overrightarrow{A_l},\overrightarrow{B_l},\overrightarrow{C_l},(x_1,y_1,z_1)$と$\overrightarrow{A_r},\overrightarrow{B_r},\overrightarrow{C_r},(x_2,y_2,z_2)$が求まりました
最初の三角形の数値の組は$(0,\frac12,1)$とします。
こうして再帰して求めたい点を全部出していきます。
そして求まった点と数値の組ですが、順番がはっきりしています。
$k$回の再帰をしたとして、点と数値の組が最初のものも含めて合計$2^{k+1}-1$個求まったとします。
点の列$(n_i,m_i)$をこう定めます。
\begin{eqnarray}
(n_0,m_0) &=& \overrightarrow{A} \\
\end{eqnarray}
$(n_i,m_i)$は求めた数値の組すべての中で真ん中の数が$i$番目に小さいものの点$\overrightarrow{A_x},\overrightarrow{B_x},\overrightarrow{C_x}$のうち、$\overrightarrow{C_x}$の座標
\begin{eqnarray}
(n_{2^{k+1}},m_{2^{k+1}})=\overrightarrow{B}
\end{eqnarray}
こうすることで求めた座標を順番どおりにできます。
(ただし$\overrightarrow{A}$と$\overrightarrow{B}$は最初の三角形のものです)
要は厳密に順番に並べたかっただけです
こうして得られた順番に並んだ点の列$(n_i,m_i)$を使って、
これらを順に直線補間していきます。
まず区間$[0,1]$を$2^{k+1}$個の区間に分けます。
どう分けてもいいですが均等に分けておきます。
\begin{eqnarray}
t_0=0,t_1=\frac1{2^{k+1}},t_2=\frac2{2^{k+1}},...,t_{2^{k+1}}=1
\end{eqnarray}
そして、各区間$[t_0,t_1],[t_1,t_2],[t_2,t_3],[t_3,t_4],...,[t_{2^{k+1}-1},t_{2^{k+1}}]$
に対して線形補間をします。
つまり、$[t_i,t_{i+1}]$においては、
\begin{eqnarray}
f_k(t)&=&\qty(1-\frac{t-t_i}{t_{i+1}-t_i})\cdot(n_i,m_i)+\qty(\frac{t-t_i}{t_{i+1}-t_i})\cdot(n_{i+1},m_{i+1})
\\&=&\frac{t_{i+1}-t}{t_{i+1}-t_i}\cdot(n_i,m_i)+\frac{t-t_i}{t_{i+1}-t_i}\cdot(n_{i+1},m_{i+1})
\end{eqnarray}
と定義します。
こうしてできた関数$f_k: [0,1] \rightarrow \mathbb{R}^2 $が
ほぼほぼ欲しかった関数です。
そう。あとは極限$\underset{k\to\infty}{\lim}$をとればいいです。
\begin{eqnarray}
f(t) = \lim_{k\to\infty}f_k(t)
\end{eqnarray}
出来ました。
おまけ
svg画像での青い部分の面積と画像全体の面積との比率を出してみます。
\begin{eqnarray}
0.15890278592375368
\end{eqnarray}
となりました。