角の二等分線の問題

はじめに

youtubeから流れてきた「角の二等分線の問題prob1」について。
なかなか悩んだので記録しておきます。

問題

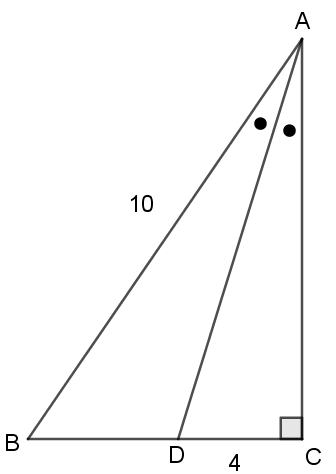
想定解

想定解は$20$とのこと。
点$\mathrm{D}$から辺$\mathrm{AB}$へ下ろした垂線の長さが$4$になるので、
面積は
$10 × 4 ÷ 2 = 20$

この三角形は存在するか

そもそも「この三角形は存在しないのでは?」 という議論があったので検討する。

まず、$\mathrm{BD}$の長さを$x$、$\mathrm{AC}$の長さを$y$とおく。また、点$\mathrm{D}$から辺$\mathrm{AB}$へ下ろした垂線の足を点$\mathrm{E}$とする。

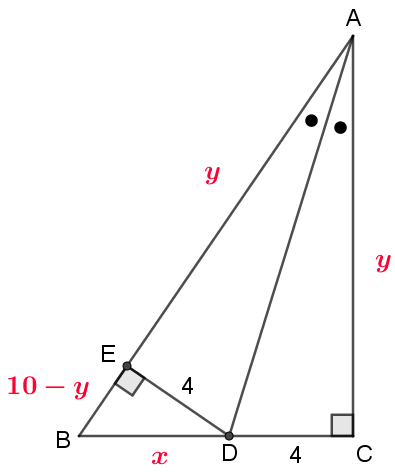
$\triangle\mathrm{ABC}$と$\triangle\mathrm{DBE}$が相似なので
$$10:x=y:4 \qquad(\mathrm{AB}:\mathrm{BD}=\mathrm{AC}:\mathrm{DE})$$
よって
$$xy=40$$
$y \lt 10$なので、上式と合わせて考えると
$$x\gt 4$$
同様に$x+4\lt10$から
$$y \gt \frac{20}{3}$$
よって、$x$,$y$は適当な正数$\alpha$,$\beta$を用いて、
$x=4+\alpha$、$y=6+\beta$
とおける。

$\triangle\mathrm{ABC}$について三平方の定理を考えると
$$(x+4)^2+y^2=100$$
$\alpha$,$\beta$を用いて式を書きかえると
$$(8+\alpha)^2+(6+\beta)^2=100$$
だが
$$8^2+6^2=100$$
であるので、
条件を満たす正数$\alpha$,$\beta$の組は存在しない。
よって、このような$\triangle\mathrm{ABC}$は存在しない。

おわりに

今回、三角形の不存在を示すにあたり、
三角不等式、正弦定理など、思いついた式を片っ端から書き出して検討ましたが、
必要十分な検討を効率よく行いたいものです。
いつか「条件をみたす三角形は存在するか」を簡便に検討する方法について考えてみたい。

おまけ

直角三角形において、角の二等分線と対辺との交点について考える。
中心が原点、半径が$r$の円を$C$とする。$C$上に点$\mathrm{P}$をとり、
$\mathrm{P}$から$x$軸へ下ろした垂線の足を$\mathrm{H}$とする。
$\angle\mathrm{POH}$の二等分線を$l$として、直線$l$と直線$\mathrm{PH}$の交点を$\mathrm{Q}$とする。
点$\mathrm{P}$が円$C$上を動くとき、点$\mathrm{Q}$の描く軌跡は下図のようになる。

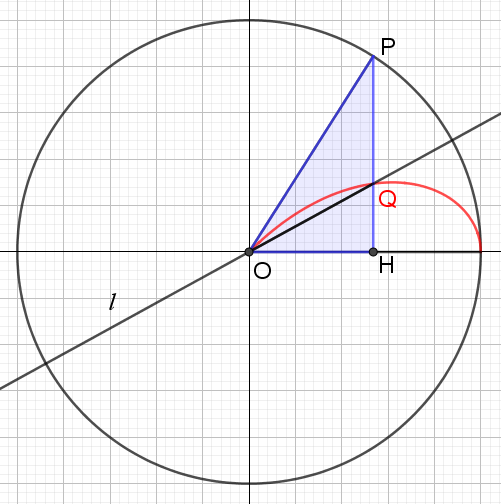
点$\mathrm{Q}$の軌跡の方程式は
$$y=x\sqrt{\frac{r-x}{r+x}}$$
この$y$が最大となるのは、$\displaystyle x=\frac{\sqrt{5}-1}{2}r$ のときで、値は、

$$ y=\left( \frac{\sqrt{5}-1}{2} \right)^{\frac{5}{2}} r\ = (0.30028310\cdots)r$$
このとき、点$\mathrm{P}$の$y$座標は
$$y_{\mathrm{P}}=r\sqrt{\frac{\sqrt{5}-1}{2}} $$
であり、
$$\mathrm{PQ}:\mathrm{QH}=1:\frac{\sqrt{5}-1}{2}$$

以上の結果から、
問題1の$\triangle \mathrm{ABC}$が存在するためには$\mathrm{CD}$の長さが$3$以下であれば良い。

$\mathrm{Q}$が描く曲線について

さらに余談だが、軌跡の方程式を整理すると
$$(x-r)x^2+(x+r)y^2=0$$
となり、このグラフはストロフォイド（葉形線）と呼ばれる曲線らしい。
軌跡としてストロフォイドの全体を得るには、直線$l$を次のようにすれば良い。
$l$:点$\mathrm{A}=(r,0)$として、$\angle\mathrm{POA}$の二等分線。

似た形の曲線に「デカルトの正葉線」と呼ばれる曲線があり、以下の式で表される。
$$x^3+y^3-3axy=0$$
グラフの形が似ているので
試しに「デカルトの正葉線」のグラフを$-\frac{\pi}{4}$回転したグラフの方程式を求めると
$$(x-A)x^2+(3x+A)y^2=0$$
の形をしている。よって、この曲線はストロフォイドとは別物であることが分かる。
※$A=\frac{3\sqrt{2}}{2}a$

似た曲線としては「マクローリンの三等分曲線(Trisectrix of Maclaurin)」なんてのもある
$$\left(x-\frac{3}{2}a\right)x^2+\left(x+\frac{1}{2}a \right)y^2=0$$