お試し
ミケル点を使おう！
はじめに
こんにちは。中学３年生、ミケル点好きのUと言います！
今日は、一緒にミケル点を使って問題を解いていきましょう！
mathlogの記事を書くのは今回が初めてなので、稚拙な文章だとは思いますが最後まで
読んでいただけると嬉しいです！
ミケル点の基本的な説明はこの記事では行いません。船旅などで一通り学んでからこの記事を読むことをおすすめします。
IMO、SLP、Japan TSTのネタバレを含みます。（IMO、SLPについては近年のものを除外してあります。）
問題
AB = ACなる二等辺三角形ABCがあり, 辺BC上の点DはBD < CD をみたす。Dから辺AB, ACにおろした垂線の足をそれぞれP,Qとする。線分PQの垂直二等分線が線分APと点Eで交わっており,三角形ABCの外接円と三角形APQの外接円がAと異なる点Fで交わっているとする。Q,E,Fが同一直線上にあるとき∠BAC = $90^{\circ}$が成り立つとを示せ。ただし,XYで線分XYの長さを表すものとする。
まずは図を描いてみましょう。
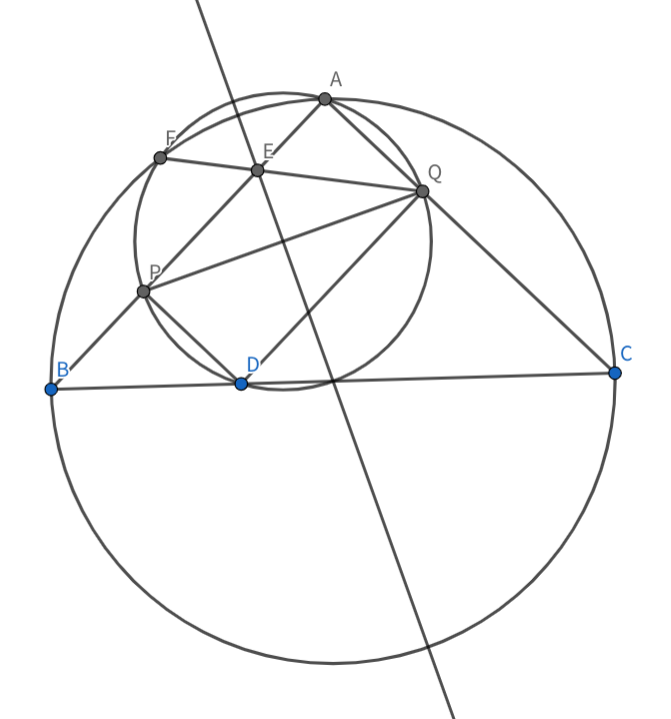
∠BAC = $90^{\circ}$なるように描くとQ, E, Fが共線に見える図が描けますね。
明らかに4点APDQは共円です。円APQと辺BCの交点をM(!＝D)とすると、∠AMD＝$90^{\circ}$より点Mは辺BCの中点であることがわかります。図を少し見てみます。点Fは完全四辺形PQCBのミケル点ですね。ゆえに三角形FPQ ∽ 三角形FBCで、線分PQの中点をNとすると、この相似においてNとMが対応します。よって、点Fは三角形FPNを三角形FBMに移す回転相似の中心なので、完全四辺形PNMBのミケル点になり、FPNEの共円がわかります。あとはangle chaseをすると、∠PFQ＝$90^{\circ}$が得られ、題意が示されます。
基本が詰まっている問題でしたね。angle chaseも簡単で解きやすかったと思います。
次行きましょう。
点Oを中心とする円が鋭角三角形ABCの辺AB、ACとそれぞれ点D、Eで交わっている。三角形ABCの外接円と三角形ADEの外接円の交点をK(!＝A)とすると、∠OKA＝$90^{\circ}$を示せ。
主張がきれいですね。図を描きます。
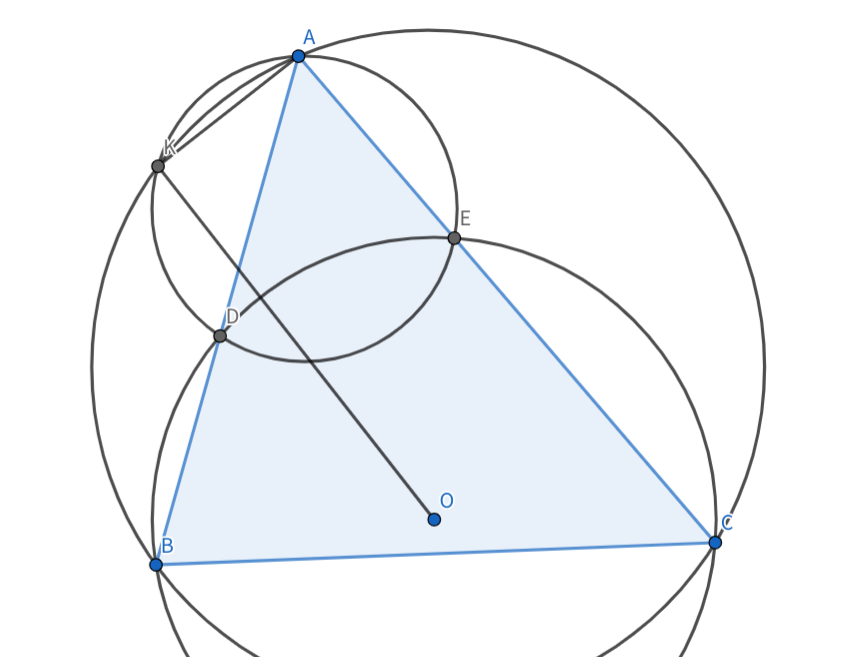
ミケル点をみっ(以下略)
点Kが完全四辺形DECBのミケル点ですね。でも、ここからどうしましょう。点Oを上手く扱いたいです。示したいことから逆算して考えるのも良さそうです。
- ミケル点は離れた中点(辺の比)を移せる
- 垂直(示したいこと)
- 点O(円の中心)
この３つを意識して考えてみます。うーん、、、あっ！！
BDとCEの垂直二等分線が刺さりそう！！
正解です！！(自問自答)
線分BD、CEの中点をそれぞれM、Nとすると∠OMA＝$90^{\circ}$、∠ONA＝$90^{\circ}$よりAMONが共円です。また、三角形KBD ∽ 三角形KCEであり、MとNが対応するので∠KMD＝∠KNEです。よって、AKMNの共円が得られます。以上より、AKMONの共円がわかるので、∠OKA＝∠OMA＝$90^{\circ}$が示されます。
また、これの特殊な場合が下の図ですね。
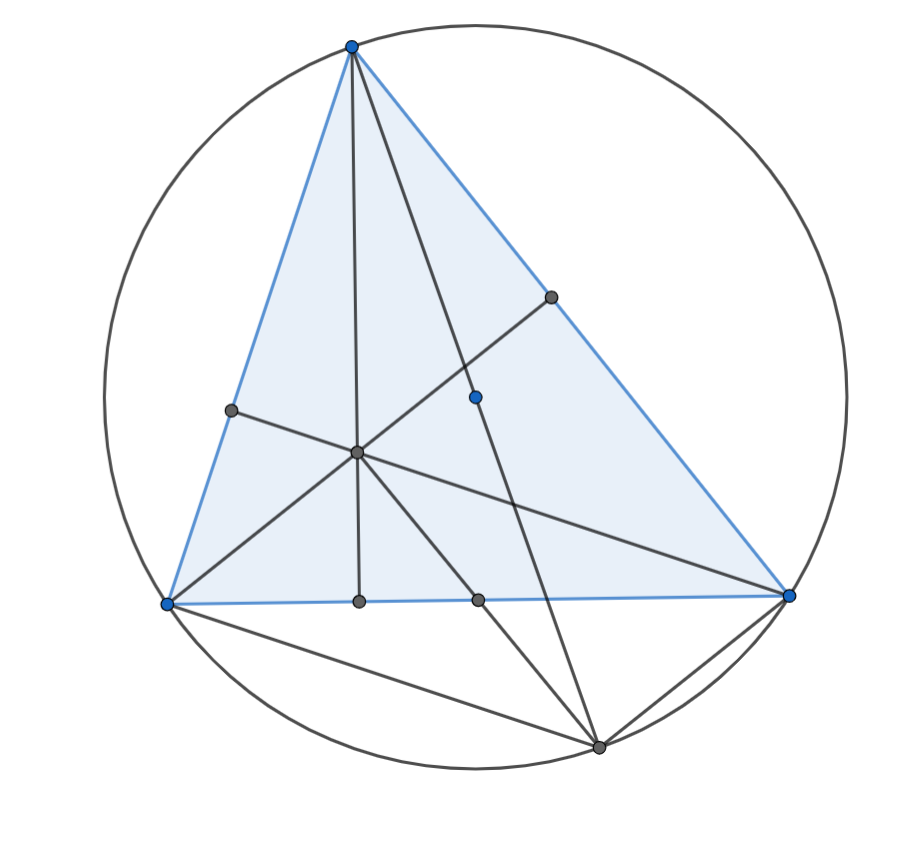垂心の某構図
さいごに
おためしでmathlogを書いてみたのですが、想像以上に時間がかかってしまいビビってます。色々使い方をミスっていることに気がついたので、近々別の記事を書こうと思います。読んでくださりありがとうございました！