高校数学解説

連結グラフの性質を多項式を使って示す話

多項式,グラフ理論

865

おはようございます。先日気持ちのいい発見をしたので、共有したいと思います。

考える問題

私はこんな問題を作ってみました．
すると，ある有名事実が帰結として得られたのです．

問題：

$n$ 頂点からなる連結グラフ $G$ が与えられます．
$G$ の全域部分グラフ $G^{'}$ であって，どの頂点の次数も偶数であるようなものはいくつありますか？

例を挙げましょう．全域とは，頂点が一致しているということです．
図の $G$ なら，右の $G^{'}$ が条件を満たすすべての全域部分グラフですから，答えは $4$ です．

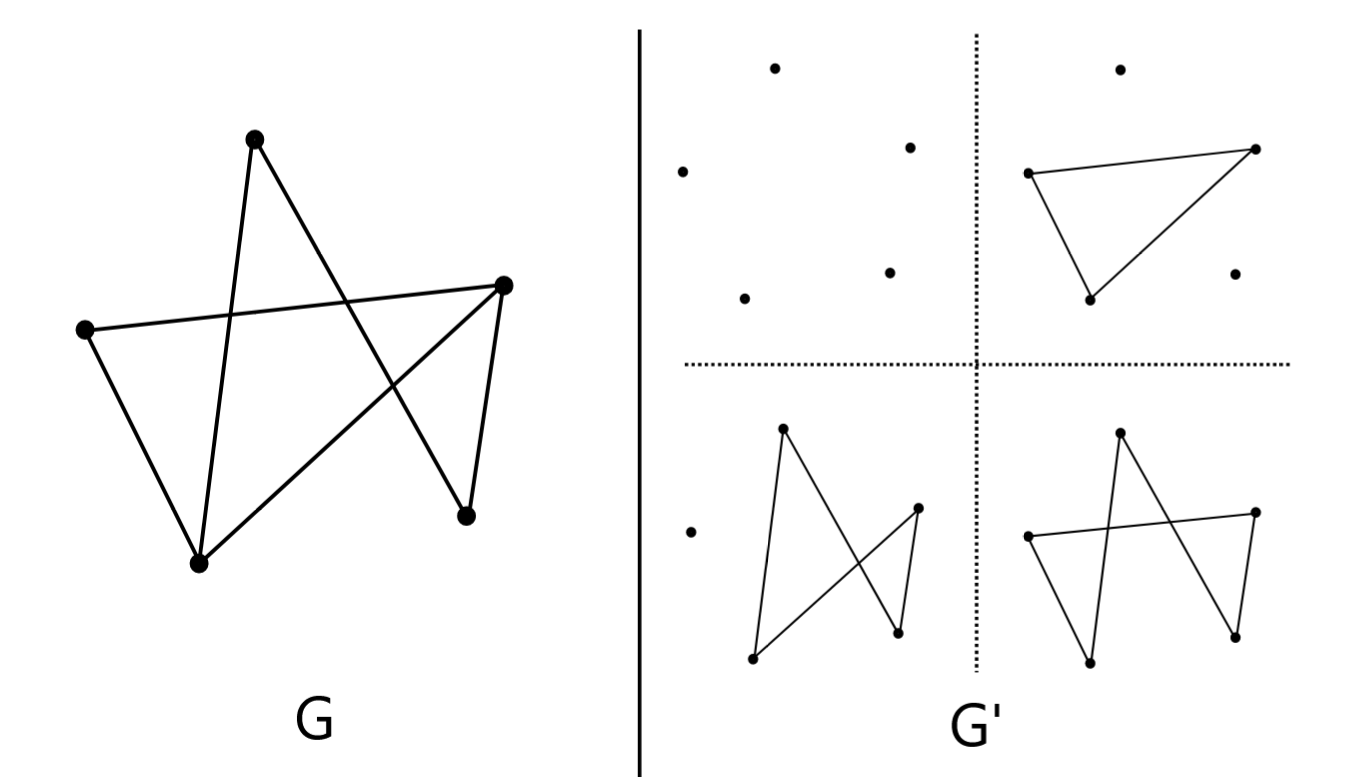5 頂点 6 辺のグラフ G の場合

では解いていきましょう．
いちごじゃむさんに勝手に倣って，シンキングタイムという名の行間を空けます．
最終的に得られる帰結が何かまで予測できた方はすごいです．私に自慢してください．

T
Th
Thi
This
This i
This is
This is G
This is GY
This is GYO
This is GYOU
This is GYOUK
This is GYOUKA
This is GYOUKAN
This is GYOUKA
This is GYOUK
This is GYOU
This is GYO
This is GY
This is G
This is
This i
This
Thi
Th
T

問題を解く

そうだ、多項式を使おう。

$G$ の頂点に $1, 2, \dots, n$ とラベル付けをしておきます．
$G$ の辺の数を $E$ とし， $i$ 番目の辺が頂点 $a_{i}$ と $b_{i}$ を結ぶものとします．いま多項式 $P$ を
$P (x_{1}, x_{2}, \dots, x_{n}) := \prod_{k = 1}^{E} (1 + x_{a_{i}} x_{b_{i}})$
で定義すると，答えは $P$ の $x_{1}, x_{2}, \dots, x_{n}$ の次数がすべて偶数である項の係数の総和で与えられます．さらにこれは，次の総和を $2^{n}$ で割ったものに等しいです．
$\sum_{p_{1}, \dots, p_{n} \in {1, - 1}} P (p_{1}, \dots, p_{n})$
これはさほど難しくなく，上の総和で， $P$ のそれぞれの項の寄与を考えれば従います．

さて， $p_{1}, \dots, p_{n} \in {1, - 1}$ であるとき， $P (p_{1}, \dots, p_{n})$ の値はどうなるでしょうか． $P$ の定義から，これが $0$ でないのは各 $i$ で $1 + p_{a_{i}} p_{b_{i}} \neq 0$ のときのみ，すなわち
$p_{a_{1}} = p_{b_{1}} ， p_{a_{2}} = p_{b_{2}} ， \dots ， p_{a_{E}} = p_{b_{E}}$
のときのみです．いま，仮定より $G$ は連結でしたから，これは次のように言い換えられます．
$p_{1} = p_{2} = \dots = p_{n}$
これは，各 $p_{i}$ たちがイコールという「辺」で結ばれている状況を考えれば分かります．
従って，考えるべき総和は，非常にシンプルで，
$\prod_{k = 1}^{E} (1 + 1 \cdot 1) + \prod_{k = 1}^{E} (1 + (- 1) \cdot (- 1)) = 2 \times 2^{E}$
になります．よって問題の答えはこれを $2^{n}$ で割った $2^{E + 1 - n}$ になります！

これで問題が解決できました．...ん？

...あれ？

問題の答えは整数であるはずです．従って，次が成立しなければいけません．
$E + 1 - n \geq 0 ⟺ E \geq n - 1$
つまり，次のことが言えます！

$n$ 頂点連結グラフの辺の本数は $n - 1$ 以上である．

さらには，条件を満たすグラフのうち１つは「辺がないグラフ」ですから，次のような同値が成り立ちます．

$E > n - 1$ $⟺$ $2^{E + 1 - n} > 1$
$⟺$ 辺が $1$ 本以上で，条件を満たす全域部分グラフが存在する
$⟺$ $G$ の部分グラフであって，どの頂点の次数も $2$ 以上の偶数であるものが存在する
$⟺$ $G$ の部分グラフであって，始点と終点が一致するように一筆書きできるものが存在する（Euler の定理より）
$⟺$ $G$ に閉路が存在する