文献あり

4点を通る2次曲線群の中心の軌跡を「自由度」から導く

235

タイトル画像　使用ツール Microsoft Copilot

はじめに

　この記事は日曜数学 Advent Calendar 2024 の $5$ 日目の記事です。

　また、 $2024$ 年 $10$ 月 $27$ 日に開催された第 $31$ 回日曜数学会で私が発表した内容をベースにした記事です。発表のときに証明しなかった部分についての証明を加筆した内容となっていますので、発表をご覧になった方もお楽しみいただけると思います。

発表スライドへのリンク: https://x.com/apu_yokai/status/1850478429734314458

　この記事では、平面上に任意にとった $4$ 点を通る $2$ 次曲線の性質について、「自由度」をキーワードにしていろいろと考察していきます。
　任意にとる $4$ 点は一般の位置にあるものとします。
　ここで「 $4$ 点は一般の位置にある」というのは、例えば $4$ 点を $A, B, C, D$ とするとき、「複数の点が $1$ 点で重なるときには成り立たない」とか、「直線 $A B$ と直線 $C D$ が平行になるときには成り立たない」のような、特殊な場合には成り立たなくなるケースについては「わずかな例外として除外して考える」というニュアンスです。

　最初に、「用語など」のセクションで「 $2$ 次曲線」や「自由度」についての説明から始めますが、この部分は読み飛ばしてもらってもかまいません。

用語など

$2$ 次曲線について

　 $2$ 次曲線というのは、

　 $A x^{2} + B x y + C y^{2} + D x + E y + F = 0$

の形の陰関数で表される曲線で、楕円、双曲線、放物線など、円錐を平面で切り取った断面の形になることから、「円錐曲線」とも呼ばれています。

　なお、 $2$ 次曲線の特殊なケースとして「正円」や「二直線」となる場合があります。

　分野によっては、正円や二直線を $2$ 次曲線に含めない場合もあるようですが、この記事では $2$ 次曲線に含めて考えます。

自由度

具体例から考える

　「解の自由度」について、まず具体例から考えてみましょう。
　つぎのような三元一次方程式について考えます。
　(係数に深い意味はないです。)

$\begin{array}{r} {\begin{cases} x + 2 y + 3 z - 2 = 0 \\ 2 x + 3 y + 3 z - 5 = 0 \\ 4 x + 2 y + z - 7 = 0 \end{cases} \end{array}$

解いてみると、解として

$x = 1, y = 2, z = - 1$

が得られます。

解となるのは1つだけで、自由に動かすことはできませんね。

式の数を１つ減らしてみるとどうなるでしょうか。

$\begin{array}{r} {\begin{cases} x + 2 y + 3 z - 2 = 0 \\ 2 x + 3 y + 3 z - 5 = 0 \end{cases} \end{array}$

これでは解は1つに定まりません。
ただし、 $x, y, z$ のどれか $1$ つを固定すれば、のこり $2$ つの変数の二元一次連立方程式となって解が1つに定まります。

例えば $z$ を固定すると $x, y$ は次の式で解が決まります。

$\begin{array}{r} {\begin{cases} x = 3 z + 4 \\ y = - 3 z - 1 \end{cases} \end{array}$

「 $x, y, z$ のどれか一つを選んで動かすと、残り $2$ つの変数は自動的に決まる」とも考えられますね。

一般化

　さて、上記の実験から、「 $n$ 元一次連立方程式の解は $n$ 個の(一次独立な)方程式があれば一意に定まる」を一般化して、「 $n$ 元一次連立方程式の解は $n - k$ 個の(一次独立な)方程式があるとき、未知数のうち $k$ 個を固定すれば一意に定まる」という予想ができますね。

　実際、これは正しくて、もう少し厳密な言い方をすると次のように書くことができます。

・　連立一次方程式の解の自由度と行列の $rank$ の関係

　 $n$ 個の未知数 $x = (\begin{matrix} x_{1} \\ x_{2} \\ ⋮ \\ x_{n} \end{matrix})$ からなる解を持つ連立一次方程式 $Ax = b$ に対して,方程式の解を全て表すために必要な任意定数の個数を解の自由度という.
また、次の関係式が成り立つ。

　　解の自由度 $= n - rank A$

　ここで太字のアルファベットはベクトルや行列を表しています。
　行列の $rank$ についてこの記事では詳しく解説しません。
　ざっくりと、「 $n$ 元一次連立方程式の解の自由度は、一次独立な係数を持つ方程式の数が $k$ 個のとき $n - k$ 」と認識してもらえれば以下の議論には十分です。
　詳しく知りたい方は参考文献をご覧ください。

$2$ 次曲線は $5$ 点で1つに定まる

　 $2$ 次曲線にはパラメータが $6$ つあります。

　 $A x^{2} + B x y + C y^{2} + D x + E y + F = 0$

　したがって、 $(x, y)$ の組が6つ、すなわち $6$ つの点があれば $A, B, ～, F$ が $1$ つに定まりそうに思えます。
　しかし、実際には $5$ つの点だけで $2$ 次曲線は $1$ 種類しかできなくなります。

　式の両辺を定数倍しても $2$ 次曲線の形は変わらないことから、自由度のうち $1$ つが「全体の定数倍」となるため、座標の位置の自由度が $6 - 1 = 5$ で自由度 $5$ になってしまうから、と考えることができますね。

!FORMULA[62][36275][0] 点を通る!FORMULA[63][36182][0] 次曲線(!FORMULA[64][36244][0] 点固定、!FORMULA[65][36151][0] 点移動) $5$ 点を通る $2$ 次曲線( $4$ 点固定、 $1$ 点移動)

Geogebraでは

　ちょっと脱線しますが、グラフ描画アプリ「Geogebra」では、ツールの中に「 $5$ 点を通る $2$ 次曲線」というものがあり、これを使うと実際に任意の $5$ 点を通る $2$ 次曲線を描くことができます。点をドラッグするとリアルタイムで $2$ 次曲線の形がグリグリ変形して楽しいです!

Geogebraのツール「!FORMULA[71][36275][0] 点を通る !FORMULA[72][36182][0] 次曲線」 Geogebraのツール「 $5$ 点を通る $2$ 次曲線」

「双曲線」になるか「楕円」になるかの境界線

　 $4$ 点を固定して $5$ 点目を動かすと、 $5$ 点を通る $2$ 次曲線は「双曲線」になったり「楕円」になったりします。「双曲線」になるか「楕円」になるかで領域を塗り分けたとき、その境界線はどんな曲線になるでしょうか。　

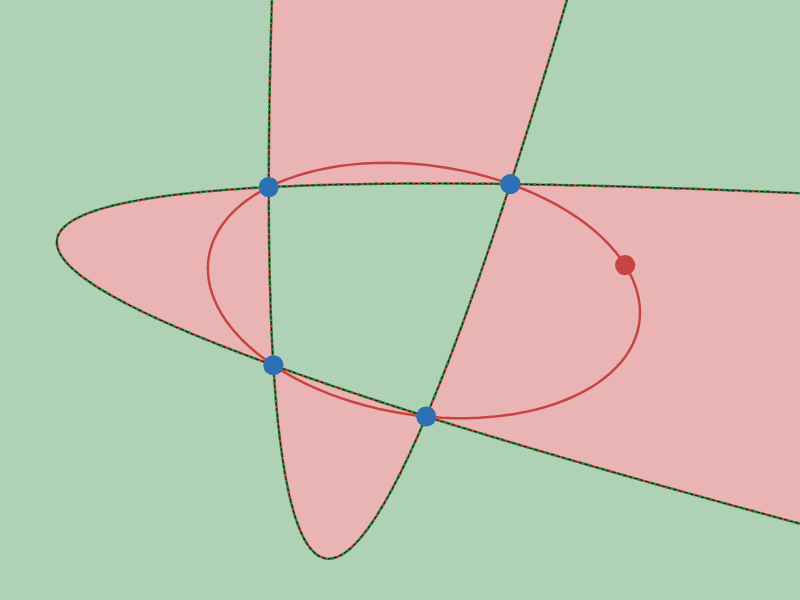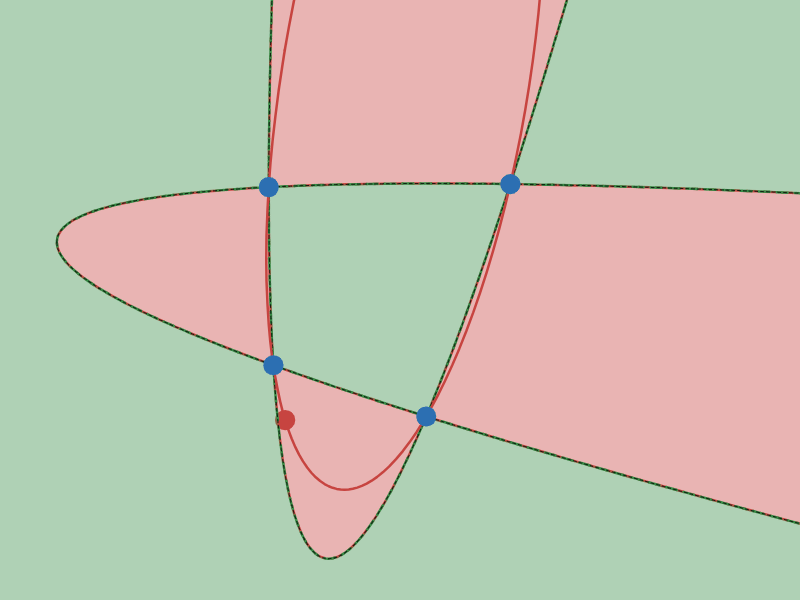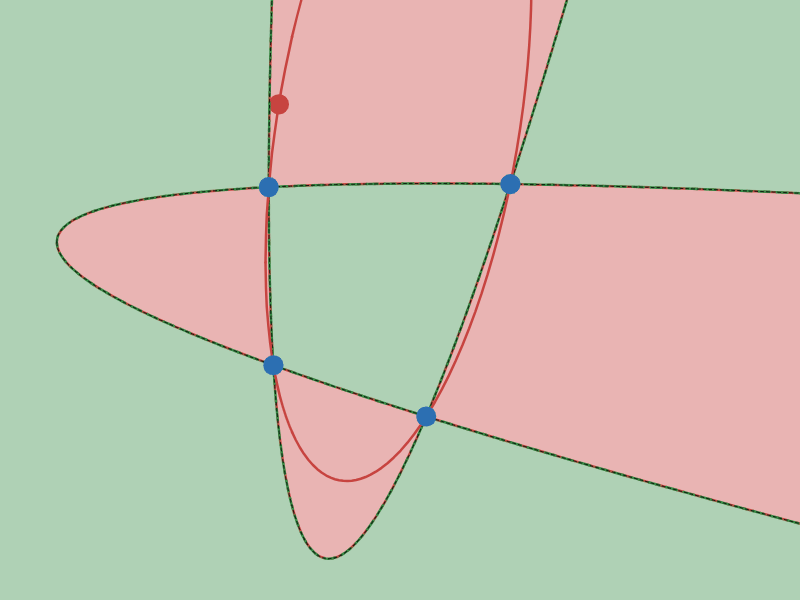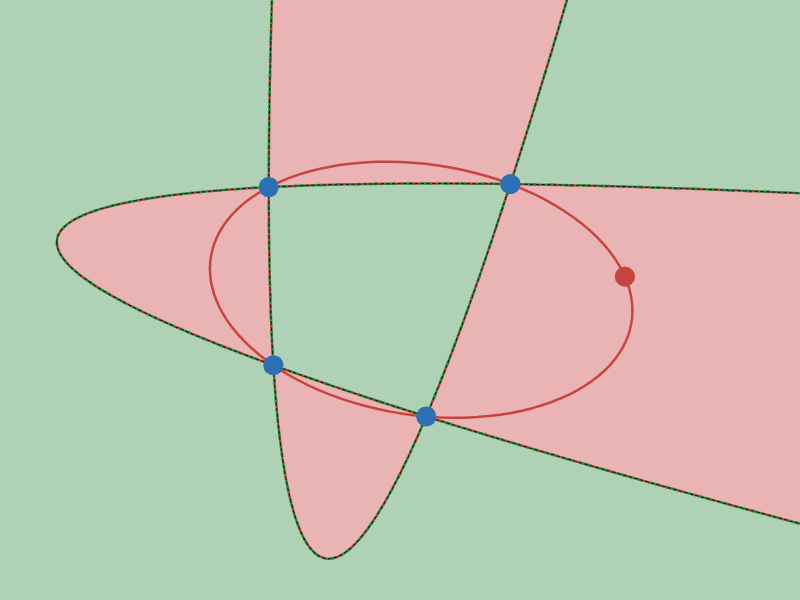双曲線と楕円の境界線は放物線となる

　図 $4$ で、緑の領域は「双曲線」になる範囲で、赤い領域は「楕円」となる範囲です。
　見てのとおり、その境界線は放物線となります。

　以前、Twitter(現X)で「4点を通る放物線は一般に2つある」というネタをポストしたことがありますが、その2本の放物線は双曲線と楕円の境界線にもなっているというわけでした。

●　そのときのポスト

任意の4点を通る放物線は0個〜2個ありますの図

なお、3点の場合は無数にあり、5点の場合は0個〜1個あります。

したがって放物線上の異なる5点の位置が分かれば元の放物線が復元できますが、4点の場合は（特殊な配置を除き）別の放物線も現れるため一意に定まりません pic.twitter.com/YRvMwP0RVb
— ａｐｕ (@apu_yokai) January 4, 2020

　
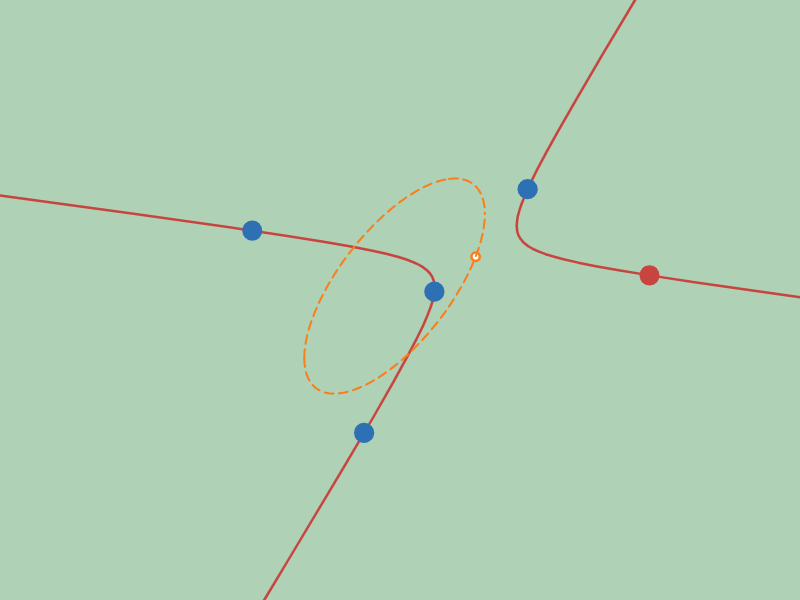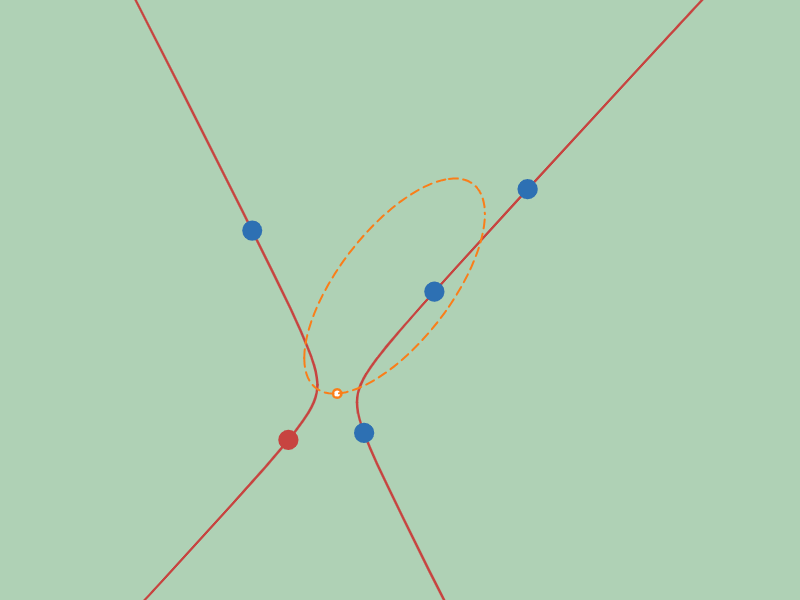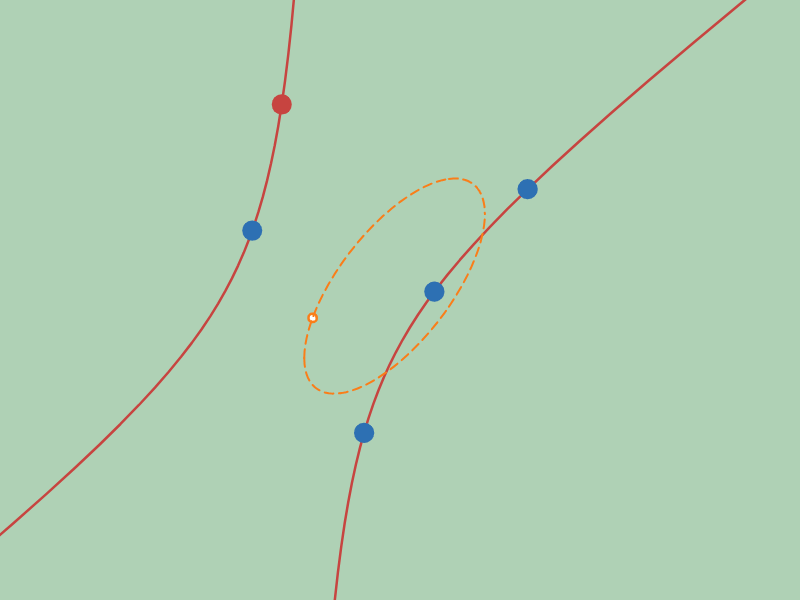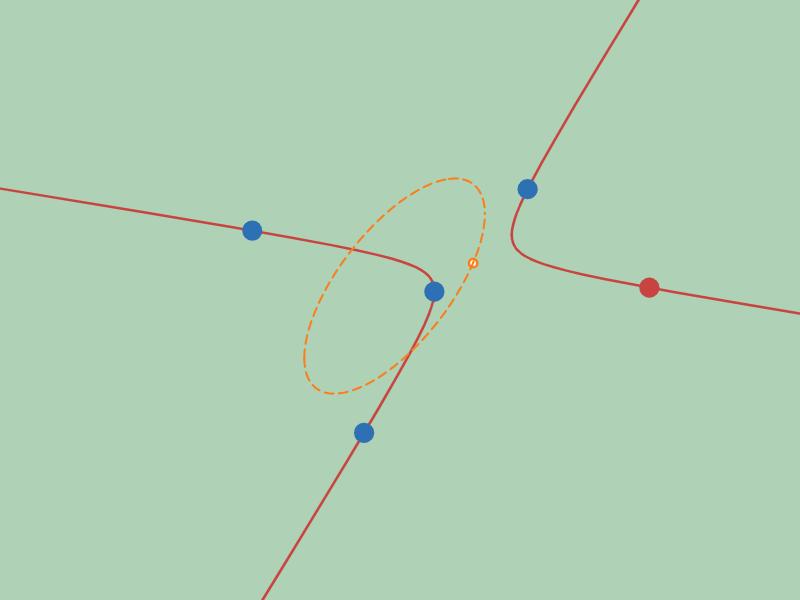
　５点目を動かすことで無数の

2

次曲線が得られますが、その「中心」の軌跡がどうなるか見てみましょう。

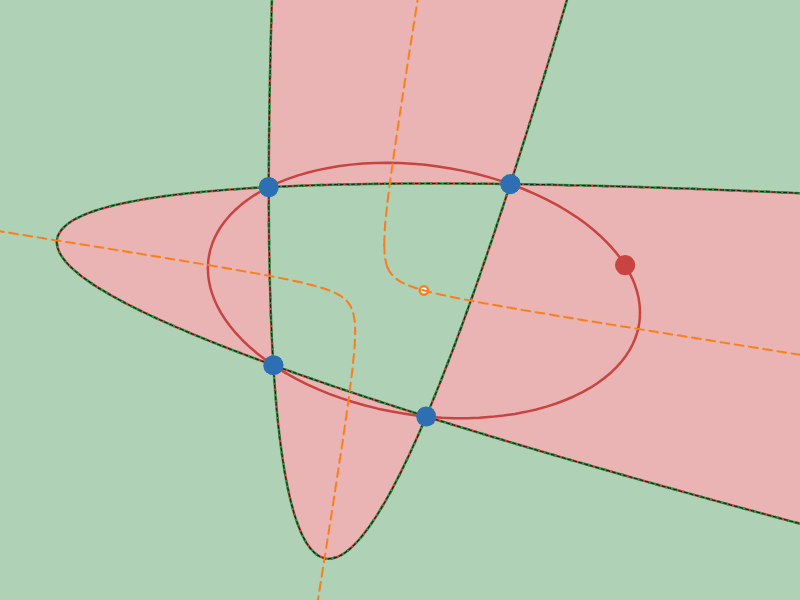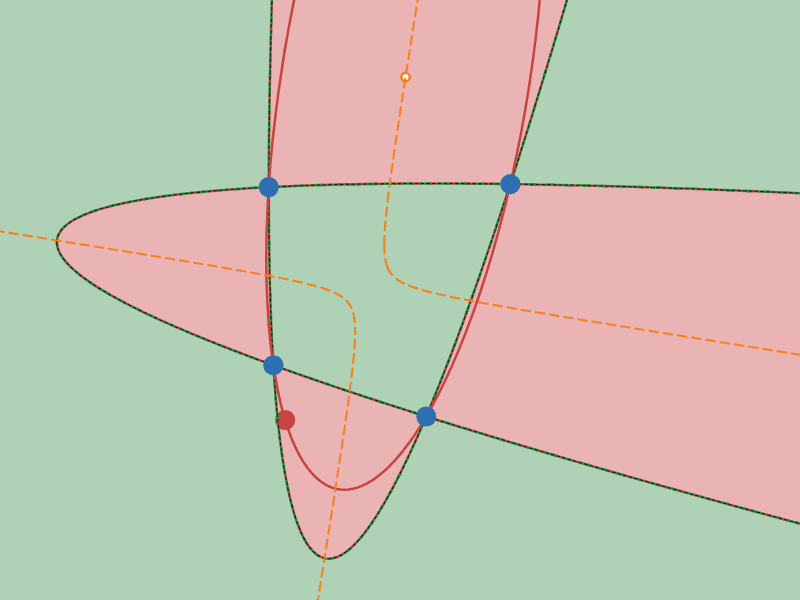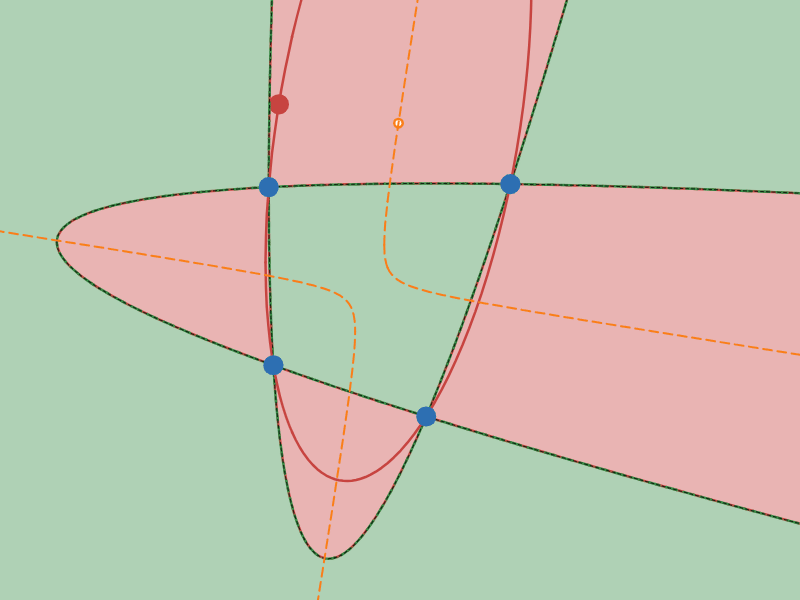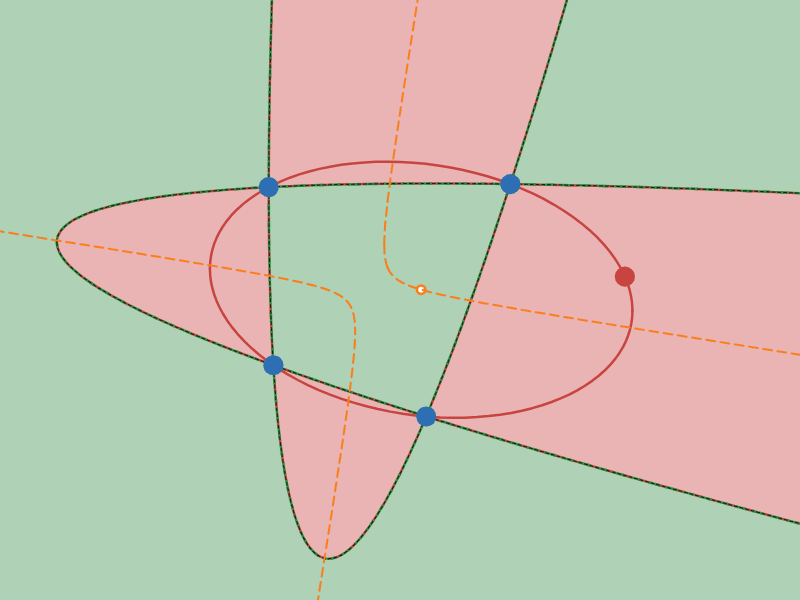「中心」の軌跡が双曲線となる配置の例

「中心」の軌跡が楕円となる配置の例

　オレンジ色の曲線が $2$ 次曲線群の中心の軌跡です。実際に $2$ 次曲線群の中心がオレンジ色の曲線の上を移動している様子を観察してみてください。

　さて、オレンジ色の曲線の形をみてください。図 $4$ では双曲線ぽく、図 $5$ では楕円ぽく見えますね?
　その直感は正しくて、実際にオレンジ色の曲線は $2$ 次曲線を描きます。

　「中心」の軌跡が楕円にるのか双曲線になるのかは、固定する4点の配置により決まります。

　図 $4$ は「4点を通る $2$ 次曲線群の中心の軌跡」が「双曲線」になる配置の例で、右図は「楕円」になる配置の例です。
　ざっくりいうと、４点が凸四角形になる配置のときは「双曲線」になり、凹四角形になる配置のときは「楕円」になります。

「中心」の軌跡と九点円錐曲線との関係

関係

　そして驚くべきことに、この「中心」の軌跡は、固定した4点に対応する「九点円錐曲線」と一致します!
　「九点円錐曲線」とは、４点に対して一意に定まる $2$ 次曲線で、４点をA,B,C,DとするとABの中点、ACの中点、ADの中点、BCの中点、BDの中点、CDの中点、直線ABと直線CDの交点、直線ACと直線BDの交点、直線ADと直線BCの交点、の合計9個の点を通る $2$ 次曲線です。

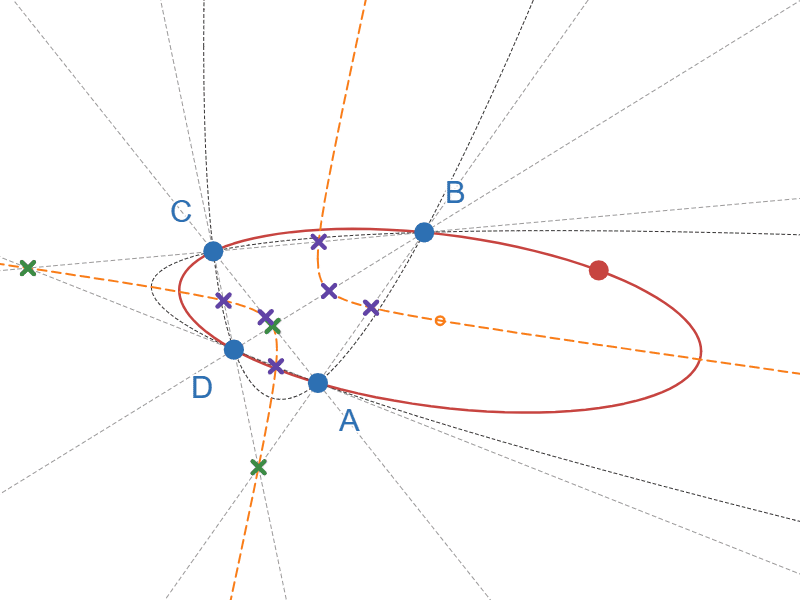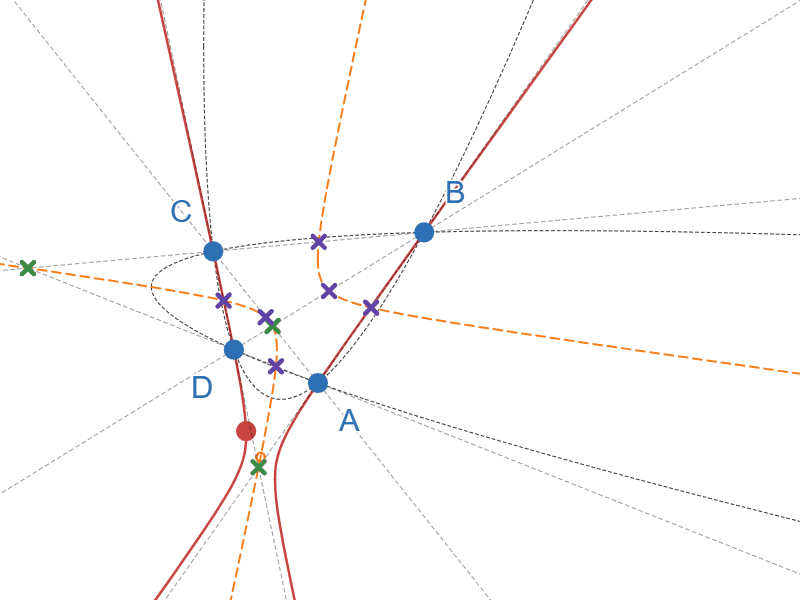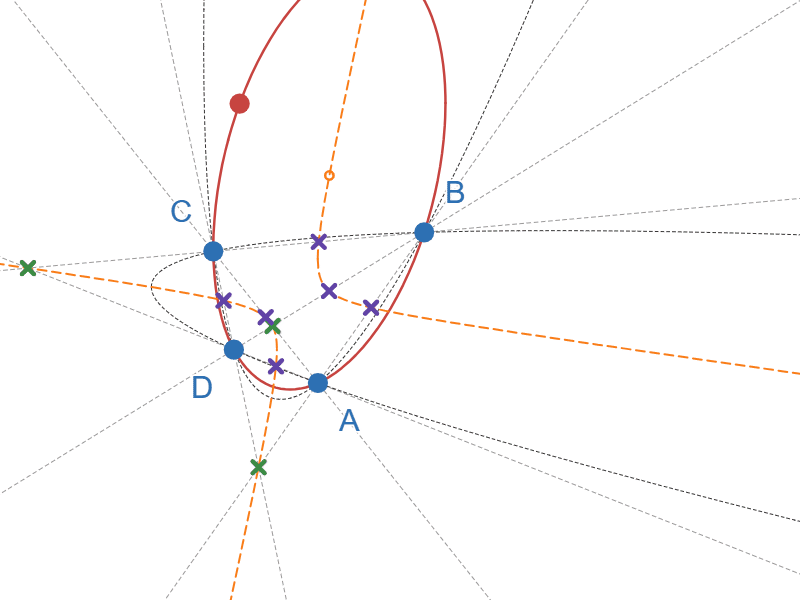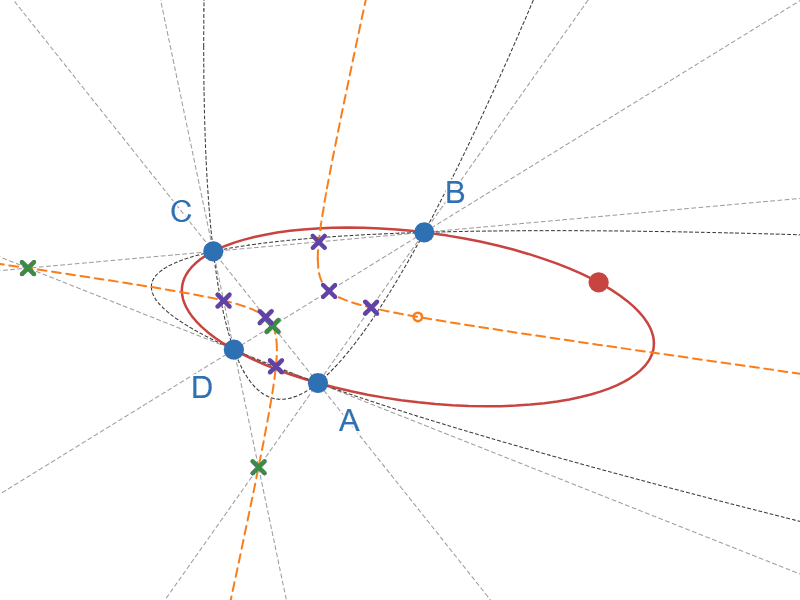九点円錐曲線が双曲線となる例

九点円錐曲線がと楕円となる例

証明

　観察したところでは確かに「中心」の軌跡と「九点円錐曲線」は一致するようですが、本当に一致するかどうか数式で確かめたいですよね!

　いろいろやってみましたが、真正面からのゴリ押し計算ではあまりにも計算量が膨大すぎてうまくいきませんでした。(膨大な計算に自信のある人は挑戦してみてね)
　そこで、ちょっとひねった方法を考えてみます。

方針

　まず、固定した $4$ 点を通る $2$ 次曲線群の中から相異なる $2$ つを適当に選んでそれぞれ $C_{1}, C_{2}$ とし、それぞれ次の式で表すことができるとします。

　 $C_{1} : A x^{2} + B x y + C y^{2} + D x + E y + F = 0$
　 $C_{2} : a x^{2} + b x y + c y^{2} + d x + e y + f = 0$

　すると、固定した $4$ 点を通る $2$ 次曲線群は次の式で表すことができます。

　 $(A x^{2} + B x y + C y^{2} + D x + E y + F) + k (a x^{2} + b x y + c y^{2} + d x + e y + f) = 0$ 　……(★)

　 $C_{2}$ 上にない点の座標が $1$ つ与えられれば、対応する $k$ は容易に求めることができます。
　そして、(★)の係数を見れば $2$ 次曲線の形になっていることは明らかですね。

　 $5$ 点を通る $2$ 次曲線は一意に定まることは先述したとおりですので、これで「固定した $4$ 点を通る $2$ 次曲線群」を表すことができることがわかりますね。

　厳密には、(★)の式では $C_{2}$ に対応する $k$ が存在しないので、「固定した $4$ 点を通る $2$ 次曲線群のうち、 $C_{2}$ を除いたもの」を表すことができることになります。 $C_{2}$ も表すことができるようにするには、変数を増やして自由度の議論にするか、場合分けするなどした方が正確ですが、簡単のためこのまま議論を進めます。

　 $k$ を動かしたとき、(★)で表される $2$ 次曲線の中心の座標を $k$ を媒介変数として表すことができます。
　この $k$ で表した中心の座標の軌跡が何らかの $2$ 次曲線に乗ることを示すことを $1$ つ目の目標にします。

　このときの「何らかの $2$ 次曲線」を「 $2$ 次曲線 $T$ 」と呼ぶことにします。　

　次に、九点円錐曲線上の点のうち $5$ つ以上がそのその $2$ 次曲線 $T$ 上にあることを示すことを $2$ つ目の目標にします。

　「 $5$ つの点があれば $2$ 次曲線は一意に定まる」のですから、これで中心の軌跡と九点円錐曲線が一致することを証明したことになります!

【証明の方針】

　 $1$ つ目の目標「 $k$ で表した中心の座標の軌跡が何らかの $2$ 次曲線 $T$ に乗ること」を示す

　 $2$ つ目の目標「九点円錐曲線上の点のうち $5$ つ以上がそのその $2$ 次曲線 $T$ 上にあること」を示す

中心の座標

　それではまず中心の座標を $k$ で表す方法を考えましょう。

　中心の座標を計算しやすいように

　　 ${\begin{cases} A^{'} = A + k a \\ B^{'} = B + k b \\ ⋮ \\ F^{'} = F + k f \end{cases}$

と置いて(★)の式を書き換えます。

　 $A^{'} x^{2} + B^{'} x y + C^{'} y^{2} + D^{'} x + E^{'} y + F^{'} = 0$ 　……(★)の書き換え

　中心の座標を $(p, q)$ とします。
　中心の座標が原点になるように $2$ 次曲線を平行移動すれば、グラフは点対称になるはずです。
　点対称になるということは、 $2$ 次曲線を表す方程式の $x$ と $y$ の係数がゼロになるということです。
　これを使って、 $p$ と $q$ の連立方程式を作り、それを解くことで $p, q$ を $A^{'}, \dots, F^{'}$ で表すことができそうです。
　さっそくやってみましょう!

　まずは中心が原点になるように平行移動して

　　　 $A^{'} (x + p)^{2} + B^{'} (x + p) (y + q) + C^{'} (y + q)^{2} + D^{'} (x + p) + E^{'} (y + q) + F^{'} = 0$

　この式の $x$ の係数は $2 A^{'} p + B^{'} q + D^{'}$ で、 $y$ の係数は $2 C^{'} q + B^{'} p + E^{'}$ なので、次の連立方程式が得られます。

　　 ${\begin{cases} 2 A^{'} p + B^{'} q + D^{'} = 0 \\ 2 C^{'} q + B^{'} p + E^{'} = 0 \end{cases}$

　 $p, q$ について解いて

　　 ${\begin{cases} p = \frac{2 C^{'} D^{'} - B^{'} E^{'}}{{B^{'}}^{2} - 4 A^{'} C^{'}} \\ q = \frac{2 A^{'} E^{'} - B^{'} D^{'}}{{B^{'}}^{2} - 4 A^{'} C^{'}} \end{cases}$

　 $A^{'} \dots F^{'}$ を元に戻して

　　 ${\begin{cases} p = \frac{2 (C + k C) (D + k D) - (B + k B) (E + k E)}{(B + k B)^{2} - 4 (A + k A) (C + k C)} \\ q = \frac{2 (A + k A) (E + k E) - (B + k B) (D + k D)}{(B + k B)^{2} - 4 (A + k A) (C + k C)} \end{cases}$

$1$ つ目の目標

( $1$ つ目の目標)
$k$ で表した中心の座標の軌跡が何らかの $2$ 次曲線に乗ることを示す

　ここまでで、 $2$ 次曲線群の中心 $(p, q)$ を $2$ つの $2$ 次曲線の係数 $A, \dots, F, a, \dots, f$ 及び $k$ で表すことができました。

　ここからは、ある定数 $r, s, t, u, v, w$ があって、 $(p, q)$ が、 $k$ の値によらず必ず

　　　 $r p^{2} + s p q + t q^{2} + u p + v q + w = 0$

を満たすことを示します。

　それはすなわち、 $k$ で表した中心の座標の軌跡が何らかの $2$ 次曲線に乗ることを示すことになるからです。
　
　それには、 $p, q$ を $k$ で表した式に書き換えて計算を進めていく必要があります。

　まともに計算しようとすると膨大な計算が必要となってしまいますので、ここでは $k$ の次数のみに注目します。

　次数のみに注目すると、 $p, q$ は次のようになります。

　　 ${\begin{cases} p = \frac{k の2次式}{k の2次式} \\ q = \frac{k の2次式}{k の2次式} \end{cases}$

　これを $r p^{2} + s p q + t q^{2} + u p + v q + w = 0$ に代入します。

　 $r {(\frac{k の2次式}{k の2次式})}^{2} + s \cdot \frac{k の2次式}{k の2次式} \cdot \frac{k の2次式}{k の2次式} + t {(\frac{k の2次式}{k の2次式})}^{2} + u \cdot \frac{k の2次式}{k の2次式} + v \cdot \frac{k の2次式}{k の2次式} + w = 0$

　ここで、この式の分母に出てくる $k$ の $2$ 次式はすべて同じ $((B + k B)^{2} - 4 (A + k A) (C + k C))$ ですから、これを二乗したものを両辺にかけることで分母をはらうことができます。

　引き続き次数のみに注目すると

　 $r \cdot (k の4次式) + s \cdot (k の4次式) + t \cdot (k の4次式) + u \cdot (k の4次式) + v \cdot (k の4次式) + w \cdot (k の4次式) = 0$

　 $k$ について降べきの順に整理すると次のような $k$ の $4$ 次式になります。

$\begin{array}{r} (r, s, t, u, v, w を含む式) \cdot k^{4} \\ + (r, s, t, u, v, w を含む式) \cdot k^{3} \\ + (r, s, t, u, v, w を含む式) \cdot k^{2} \\ + (r, s, t, u, v, w を含む式) \cdot k \\ + (r, s, t, u, v, w を含む式) = 0 \end{array}$

　この式が $k$ についての恒等式となるような $r, s, t, u, v, w$ が(定数倍の差を除いて) $1$ つだけ存在することを示します。
　「 $k$ についての恒等式となる」ということは、上記の $k$ の $4$ 次式の係数がゼロになることを意味しますから、 $r, s, t, u, v, w$ についての方程式が $5$ つ得られます。

　未知数が $6$ つで、方程式が $5$ つですから、これでは未知数が一意に定まらなさそうですが……この形、先ほどもでてきましたね?

　自由度で考えると、自由度は $6 - 5 = 1$ となります。しかし、もともとの式の形

　　　 $r p^{2} + s p q + t q^{2} + u p + v q + w = 0$

　を見れば、全体を定数倍にする自由度があることがわかります。
　したがって、 $r, s, t, u, v, w$ は(全体を定数倍する自由度があるので)一意には定まりませんが、 $2$ 次曲線としては $1$ つだけが条件を満たすことになります。

　こうして得られた $2$ 次曲線を $T$ とします。

$2$ つ目の目標

( $2$ つ目の目標)
九点円錐曲線上の点のうち $5$ つ以上がそのその $2$ 次曲線 $T$ 上にあること示す

　円錐曲線の自由度 $6$ のうち、中心点の座標で自由度 $2$ を使うと残りの自由度は $6 - 2 = 4$ となります。

　このことは、先ほどと同じ手順で $2$ 次曲線の中心が原点にくるように平行移動すると方程式の $x$ と $y$ の係数がゼロになって

　　 $A x^{2} + B x y + C y^{2} + F = 0$

となることからわかります。

　ここからさらに定数倍の自由度 $1$ を引くと、残りの自由度は $4 - 1 = 3$ となります。

　したがって、「中心の座標と、曲線上の点を $3$ つ」与えられれば $2$ 次曲線が一意に定まることになります。

　ここで「九点円錐曲線」の「九点」について振り返ってみると、そのうち $3$ 点は $4$ つの点を $2$ 組に分けてそれぞれの点の組を通る $2$ 本の直線の交点で、残りの $6$ 点は $4$ つの点のうち $2$ つの点の中点でした。

　まず、 $2$ 本の直線の交点となる方は、「2直線は2次曲線」であることを考えれば、その中心ですから、当然に $2$ 次曲線 $T$ 上にあることになります

　次に、 $2$ つの点の中点となる方は、 $4$ 点のうち $2$ 点がその点からみて点対称の位置になることから、自由度
に対する影響は $1$ 点の分しかなく、「中心の座標と、曲線上の点を $3$ つ」が与えられていることになりますから、 $2$ 次曲線が $1$ つ定まります。結果として $4$ つの点を通る $2$ 次曲線の中心となることができますから、これもまた $2$ 次曲線 $T$ 上にあることになります。

　結局、九点円錐曲線の $9$ 点全てが $2$ 次曲線 $T$ 上にあることがわかりました。

　「 $5$ つの点があれば $2$ 次曲線は一意に定まる」のですから、これで中心の軌跡と九点円錐曲線が一致することを証明できました!

「焦点」の軌跡

　最後に $2$ 次曲線群の「焦点」の軌跡です。
　ゴリ押し計算で焦点の軌跡を描くことに成功したのですが、なんとも奇妙な曲線が現れました。
　楕円をゆがめたような曲線や、双曲線をゆがめたような曲線を3つ掛け合わせたみたいに見えます。
　また、双曲線群の焦点の軌跡は楕円をゆがめたような曲線に、楕円群の焦点の軌跡は双曲線をゆがめたような曲線になっているようです。
　これらがどういう曲線なのか、何か面白い性質があるのか気になりますね!

焦点の軌跡の例!FORMULA[247][36151][0] 焦点の軌跡の例 $1$

焦点の軌跡の例!FORMULA[248][36182][0] 焦点の軌跡の例 $2$

　この「焦点の軌跡をどうやって求めたか?」についてもなかなか面白い話題だと思いますが、締め切りに間に合いそうにないので今回はここまでにします。

　興味のある方はどうすれば二次曲線の係数から焦点の座標を計算できるか考えてみてね!
　数学パズルとしてもそれなりに面白いと思います。
　(「おわりに」のセクションにある私のDesmosファイル内の数式を解析すればわかっちゃいますけどね)

【2024.12.24追記】
二次曲線の係数から焦点の座標を計算する方法について記事を書きました!
記事へのリンク：二次曲線の焦点の座標を係数から計算する

九点円錐曲線と九点円の関係

　このセクションは日曜数学会のときに「おまけ」として付け加えた内容です。
　「こんな質問が来るかな」と予想していたら、本当に質問されてとても嬉しかったです。
　
　何かというと、「九点円」という割と知られた幾何学の図形があるのですが、「九点円錐曲線」と名前が似ているので、何か関係があるのか、という質問です。

　結論からいうと、深い関係があります!

　まず、「九点円」について説明しましょう。

　任意の三角形 $A B C$ において、「 $3$ 辺の中点 $D, E, F$ 」「垂線の足 $G, H, I$ 」「垂心と $3$ 頂点の中点 $J, K, L$ 」が同一円周上にあることを「九点円の定理」といい、このときの円を「九点円」と呼びます。

　九点円錐曲線は４点から定まる $2$ 次曲線ですが、点の1つを他の３点からなる三角形の垂心になる位置にもってくると、真円になります。これが九点円と一致します。
　つまり、九点円錐曲線は九点円を一般化したものといえそうですね!

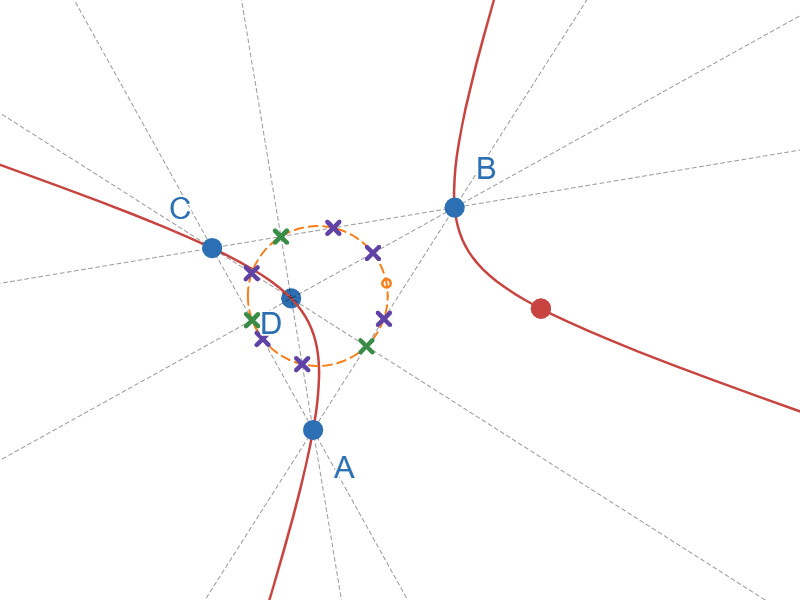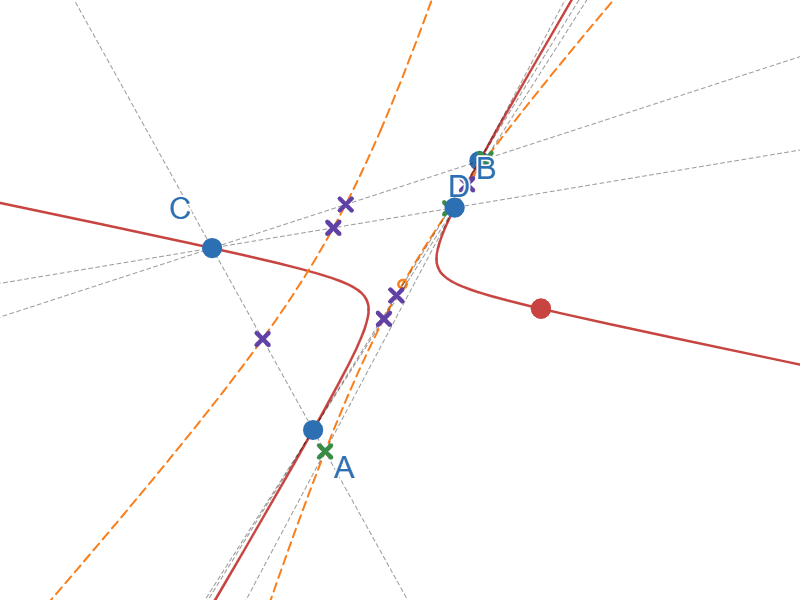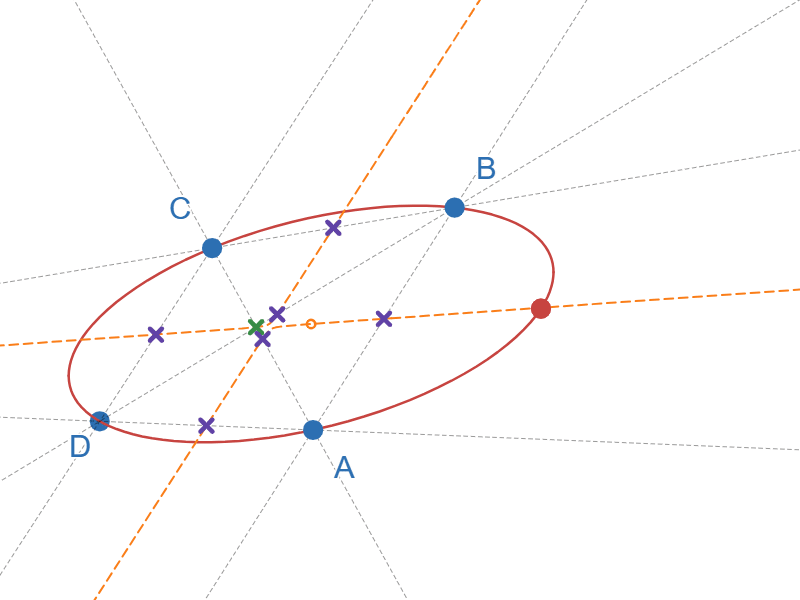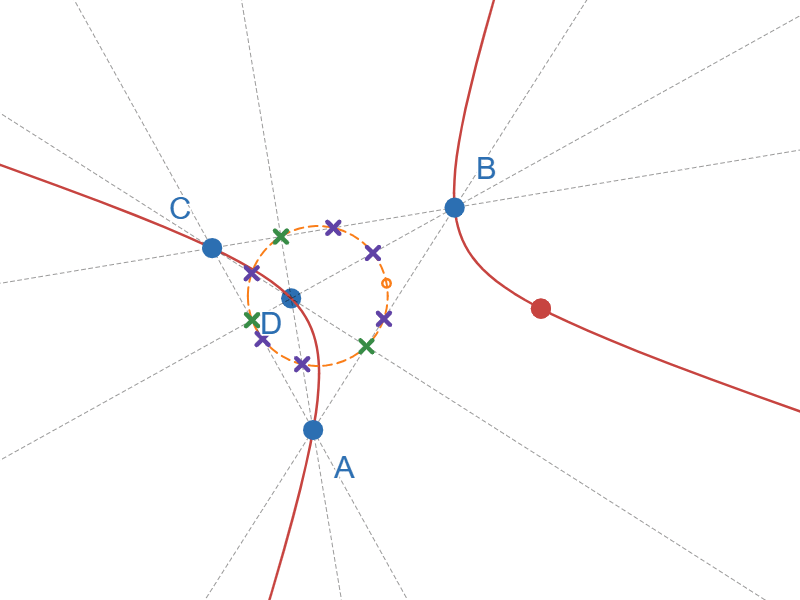九点円錐曲線と九点円の関係

　図11では点Dが△ABCの垂心の位置に来た時に一時停止するようにしています。九点円錐曲線が九点円になっていることが分かると思います。

おわりに

　これでこの記事はおわりです。
　最後に、記事を作るために作ったDesmosファイルへのリンクを貼っておきます。

Desmos:5点を通る二次曲線　4点を固定したときの中心と焦点の軌跡≪記事作成用≫

　4点を自由に動かせます。"auto" のパラメータを $0$ にすれば、5点目も自由に動かせます。九点円錐曲線の九点や、「中心」の軌跡、「焦点」の軌跡、 $4$ 点を通る放物線の様子を観察することができます。いろいろ遊んでみてください。

　今回も、Twitter(現X)でのやりとりが発表内容のベースとなっています。色々な情報や意見を頂き感謝します。
　特に、K. Miyamoto ( @KMiya3114 ) さんから教えていただいた「九点円錐曲線」はとても興味深い対象だと思います。
　大いに参考になりました。ありがとうございました。

【関連ポスト】 https://x.com/KMiya3114/status/1839239103155679350

　また、「 $2$ つ目の目標」の部分については TokusiN ( @toku51n ) さんのポストを参考にさせていただきました。ありがとうございました。

【関連ポスト】 https://x.com/toku51n/status/1852930805292790245

　発想のきっかけとなったのは　miyamath ( @miyamath84 ) さんのこのポストでした。

【関連ポスト】 https://x.com/miyamath84/status/1838927657901359438

　そのほかにも、色々なポストを参考にさせていただいています。
　今後ともよろしくお願いいたします。

　この記事に関連して、何か面白そうな発見などありましたらご連絡いただければ幸いです。