0
高校数学解説
某botさんの問題を解く[2][3]
22
0
この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。
整数問題botさんの問題を解きたいと思います
(まずかったら消します)
あまりうまい解き方ではないと思います

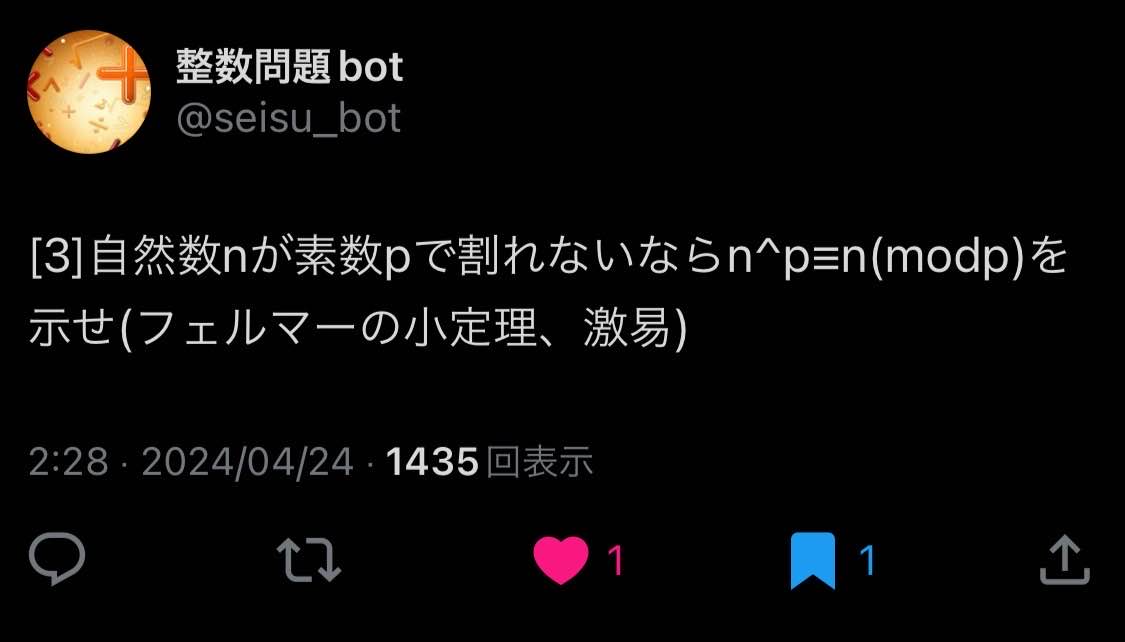
[
(Ⅰ)
(Ⅱ)
となり
(Ⅲ)nが偶数のとき
(
(
(
となり
以上より
(余談)
自然数に
以下
この場合の解は
[
以下法を
ここで
(★)
よって
となり数学的帰納法により成立(おわり)
激易でも解けない問題ちらほらあって更新続けるの厳しいかもしれません
投稿日:2024年12月30日
更新日:1月1日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中