東大寺学園数学研究部　懸賞問題解説１

はじめに

東大寺学園で2023年9月9,10日に開催した文化祭で企画した懸賞問題の解説記事です．今回は大変多くの方に解いてもらうことができました．
難易度的に例年より難しめのものになったらしいです．

1　　RESONANCEな数についての問題

問題

ある正整数が「RESONANCEな菁々数」であるとは,その数の各位の和と各位の積の合計がその数自身と等しくなるようなものをいいます．例えば59は59＝(5+9)+(5×9)なのでRESONANCEな菁々数です．RESONANCEな菁々数は有限個存在することが証明できるので,その総和を求めてください．

一言

59回文化祭ということで59にまつわる問題を1番に置きました．

解説

適当に不等式評価をして2桁以下であることを示します．
ｍが条件を満たす数としてその最高位の数をａ,桁数を桁数をｎとします．すると、以下の評価ができます．
$$9^{n-1}a+a+9(n-1)≧m≧10^{n-1}a$$
つまり
$$9^{n-1}+1+9(n-1)≧10^{n-1}$$
を満たさなくてはならず

n>3のとき存在せず,n=3のときa=1,また、n=1は明らかに不適です．
実際にn=3a=1で方程式を立てて試せば存在しないことがわかるのでn=2
その数をabとすると,
$$10a+b＝ab+a+b$$
よって,b=9です．よって,求める答えは
19＋29＋・・・+99＝531
となります．

６　　　ビルの見通し度に関する問題

問題

T町とJ町はD通りという道でつながっています．D通りには高さの異なる2023軒のビルが1列に並んで建っています．このD通りのビルの高さの関係性は2023！通り考えられることになりますが,それぞれの高さの関係性についてその「見通し度」を「（T町から見えるビルの数）+（J町から見えるビルの数）」で定めます．このとき、高さの関係性2023！通り全てにおける見通し度の合計はMと表せるので,Mが2で割り切れる最大回数を求めてください．ただし,あるビルが「町から見える」とは町から見て手前にそのビルよりも高いビルがないことをいいます．

一言

頭の良くなるゲームというものでビルを建てていくものがあって、そこから着想を得ました．
主客転倒でも解けるらしいですが,想定解では漸化式を立ててみました．

解説

$$まず,ｎこのビルの並べ方すべてについての見通し度の合計をa_nとします．$$
ここで、どのどのビルよりも小さいビルを加えて漸化式を立てます．
$$a_{n+1}＝2×n!+a_n(n+1)$$
$$b_n=\frac{a_n}{n!}とおいて$$
$$b_{n+1}=b_n+\frac{2}{n}$$
となるので、
$$a_{2023}＝2(\frac{1}{1}+\frac{1}{2}+・・・+\frac{1}{2023})×2023!$$
となり、これは2で2005回割り切れます．
（ただし,分数の和の部分が$$\frac{奇数}{奇数×1024}$$
の形で表されることを利用しました．）

８　　解が多いディオファントス方程式

問題

以下の条件を満たす正整数(x,y,z)の組をすべて求め,x+y+zの総和を求めてください．
・(x+y)(y+z)=2xz
・max(x+y,y+z,z+x)≦59
・GCD(x+y,y+z,z+x)=1

解説

1つめの式は以下のように変形できます．
$$(x+y)^2+(y+z)^2=(x+z)^2$$
また、3つ目の条件からこれらは原子ピタゴラス数であり、互いに素な自然数m,nによって
$$(x+y,y+z,z+x)＝(m^2-n^2,2mn,m^2+n^2,),(2mn,m^2-n^2,m^2+n^2,)$$
と表すことができ,$$m^2+n^2≦59$$
に注意して答えは,
(2,1,3),(4,3,21),(3,2,10),(5,3,12),(14,6,15),(5,4,36),(7,5,30),(18,10,35)とそのx,zを入れ替えたものです．

７　　　幾何

問題

三角形ABCの外接円上でAを含む弧BCの中点をM,とします．また,三角形ABCの外心をO,垂心をHとし,AHとBCの交点をDとするとき,AM=5,MH=9,OD=6が成立しました．この時HDの長さを求めてください．

一言

三平方からのごり押し解法で解いてくれた方が多かったですが,ここでは想定解を示します．

解説

以下の図のようにMO,HDと外接円の交点をF,GとしたときMO＝OFまた垂心の基本性質からHD＝DGが成り立つので,MFとHGが平行であることと合わせてMH,OD,FGは1点Xで交わります．

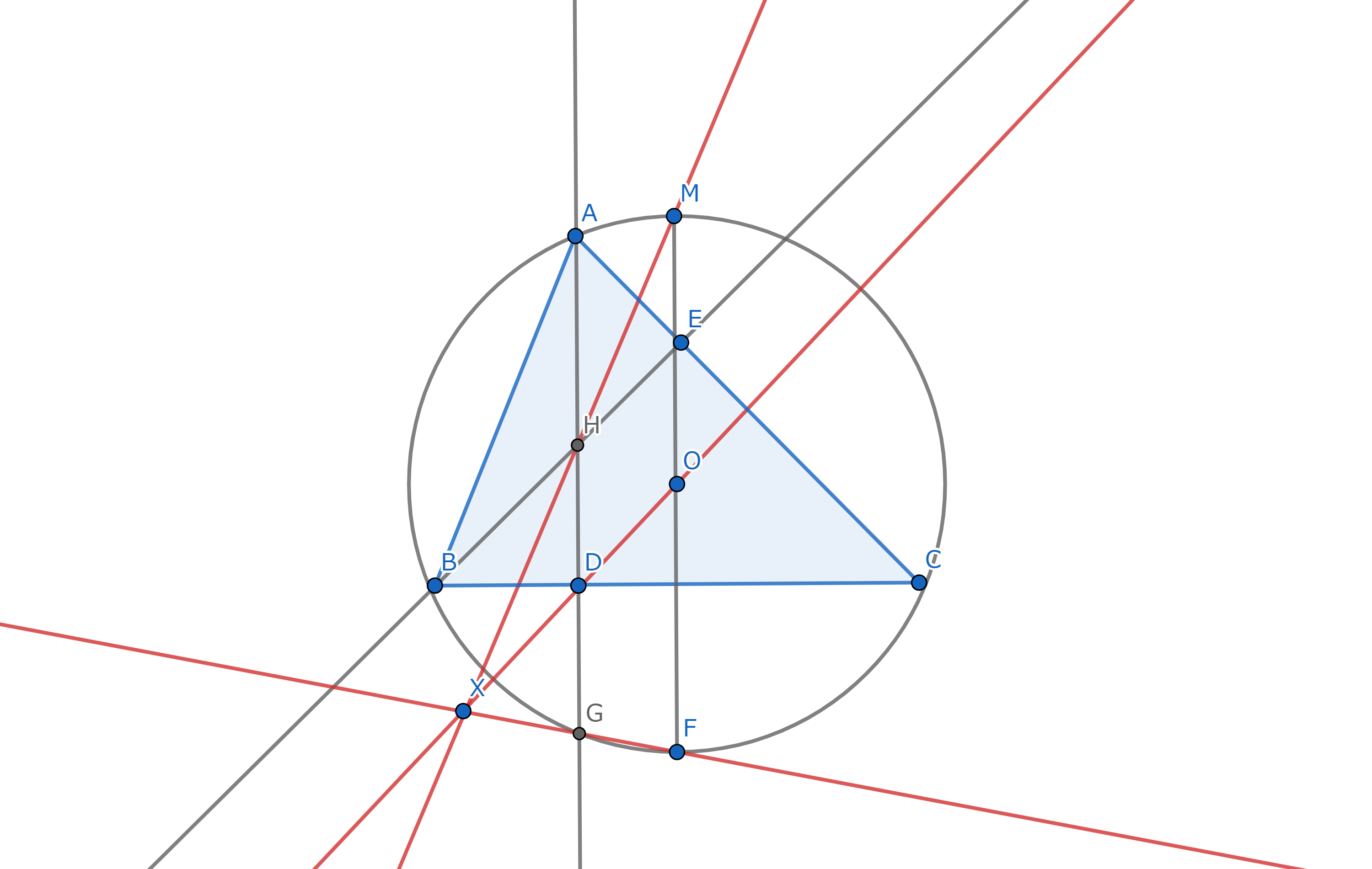
ここで,MFとHGが平行であることからAM＝GF＝5がなりたち,△XHG∽△XMFが成り立つので、XH=9x,XD＝6x,XG＝5xが成り立ち,中線定理から$$HD＝\sqrt{17}x$$です．よって外接円の半径は
$$OF＝\sqrt{17}(1+x)$$と表すことができます．
ここで,Xに対する方べきの定理から,
$$XG・XF＝XD・(XO+OF)つまり 5x・(5x+5)＝(6^2-\sqrt{17}^2)・(1+x)^2$$
$$x=\frac{19}{6}$$
とわかり,答えは$$\frac{19\sqrt{17}}{6}$$

10　　　やり取りの問題

問題

TDJ村には2023人の村人が住んでおり,名前を１郎、2郎、３郎、…、2023郎といいます．あるとき1郎は,TDJ村の紙幣である１シビを手に入れました．ここで,徳を積もうと思った村人たちは以下の行動を繰り返し2022回行いました．
行動：ｎ郎は自分が持っているシビをすべてｎ+１郎に渡す．
しかし,その行動をみていた大仏様は感動し,以下の褒美を与えました．
褒美：ｍ回目の行動のあとそれぞれの村人に行動で渡したシビのｍ+１倍のシビを与える．
さらに,大仏様はそれぞれの村人の行動の回数に応じて以下の恩恵を与えました．
恩恵：それぞれの村人が持っているシビを$$2^{シビを1つ以上渡した行動の回数}$$倍にする．
このとき,全ての村人が持っているシビの合計をＭとしたとき,Ｍが3で割り切れる最大回数を求めてください．

一言

実験をして書き出してみると法則がつかめるかもしれません．

解説

以下のことは行動の定義をよく見るとわかります．
最終的にｎ郎が持っているシビの数は
・f(x)=(x+2)(x+3)・・・(x+2023)の$$x^{n-1}$$の係数に対応している．
ここで、最後の恩恵を考えると,最終的にシビの総和は$$2^{2022}f(\frac{1}{2})$$で表されることがわかるので、
5×7×・・・4045×4047が3で割り切れる回数を考えればよく求める答えは,
$$v_3(4047!)-v_3(2023!)-1=1011$$

14　　　関数方程式×幾何

問題

正整数に対して定義され,正の実数値を取る関数f(n,m)は以下を満たします．
・f(n,m)＝f(m,n)
$$・n\equiv a,m\equiv b\left(mod6\right)ならばf(n,m)=f(a,b)$$
$$・f\left(n,n+2\right)^2＝f(n,n+1)^2+f(n+1,n+2)^2+f(n,n+1)f(n+1,n+2)$$
$$・f\left(n,n+3\right)^2＝f(n,n+1)^2+f(n+1,n+2)^2+f(n+2,n+3)^2+f(n,n+1)f(n+1,n+2)+f(n+1,n+2)f(n+2,n+3)-f(n,n+1)f(n+2,n+3)$$

このとき,(1,2,3,4,5,6)の順序付き部分集合(a,b,c,d)について,その部分集合の良し悪しを以下で定めます．

・a<b<c<dまたはa<c<d<bが成り立つときその集合は良い集合,a<c<b<dが成り立つときその集合は悪い集合と呼ぶ．

良い集合,悪い集合それぞれに対するf(a,b)× f(c,d)の総和をA,Bとおきます。このとき,AとBの大小を比較し,それが恒等的に成り立つことを証明してください．また,等号成立条件も求めてください．

一言

この問題の関数はまずf(0,1),f(1,2),f(2,3)が決まれば一意に定まることはすぐわかりますが,これを後半の不等式パートにどうつなげていくかを考えるのがテーマです．

解説

1つめの条件,また3つ目の条件から距離の関係にあることに注意します．
cf)距離の公理
a,bの距離をd(a,b)と表すと、

・d(a,a)=0
・d(a,b)=d(b,a)
・d(a,b)+d(b,c)≧d(a,c)（三角不等式）

ここで、以下のような各角度が120°であるような6角形を考えます．

上の6角形についてf(n,m)は、$$n\equiv a,m\equiv b\left(mod6\right),a,b\in(1,2,3,4,5,6)$$
としたときのa,bの距離として表されることが以下よりわかります．
まず、2つめの条件からベクトルを考えることで辺の長さがf(n,n+1)であるような6角形が存在することがわかります．
次に,数値が２つ離れているf(n,n+2)は（例えば2,4・6,2）3つ目の条件から余弦定理よりその距離であることがわかります．また、4つ目の条件から、数値が3つ離れているf(n,n+3)がその距離であることも分かります．ただし、上図において△A16,B23,C45は正三角形なので、d(B,4)＝d(2,3)+d(3,4)などが成り立つことに注意しました．
ここで、f(n,m)が図形的に定義できたので後半の不等式パートに移ることにしましょう．まず頂点の関係から以下の事実が成り立つことは明らかです．

・線分abと線分bcは良い集合の場合交点を持たず,悪い集合の場合交点を持つ．

よって、問題は以下のように一般化できます．

問：任意の凸6角形について、その対角線と辺のうち2つのの組についてその長さの積をその組の大きさとする．（ただし,その2つの線分は端点を共有しない）ここで,組であってそれらが交点を持つすべての総和と持たないものの総和の大小を比較せよ．

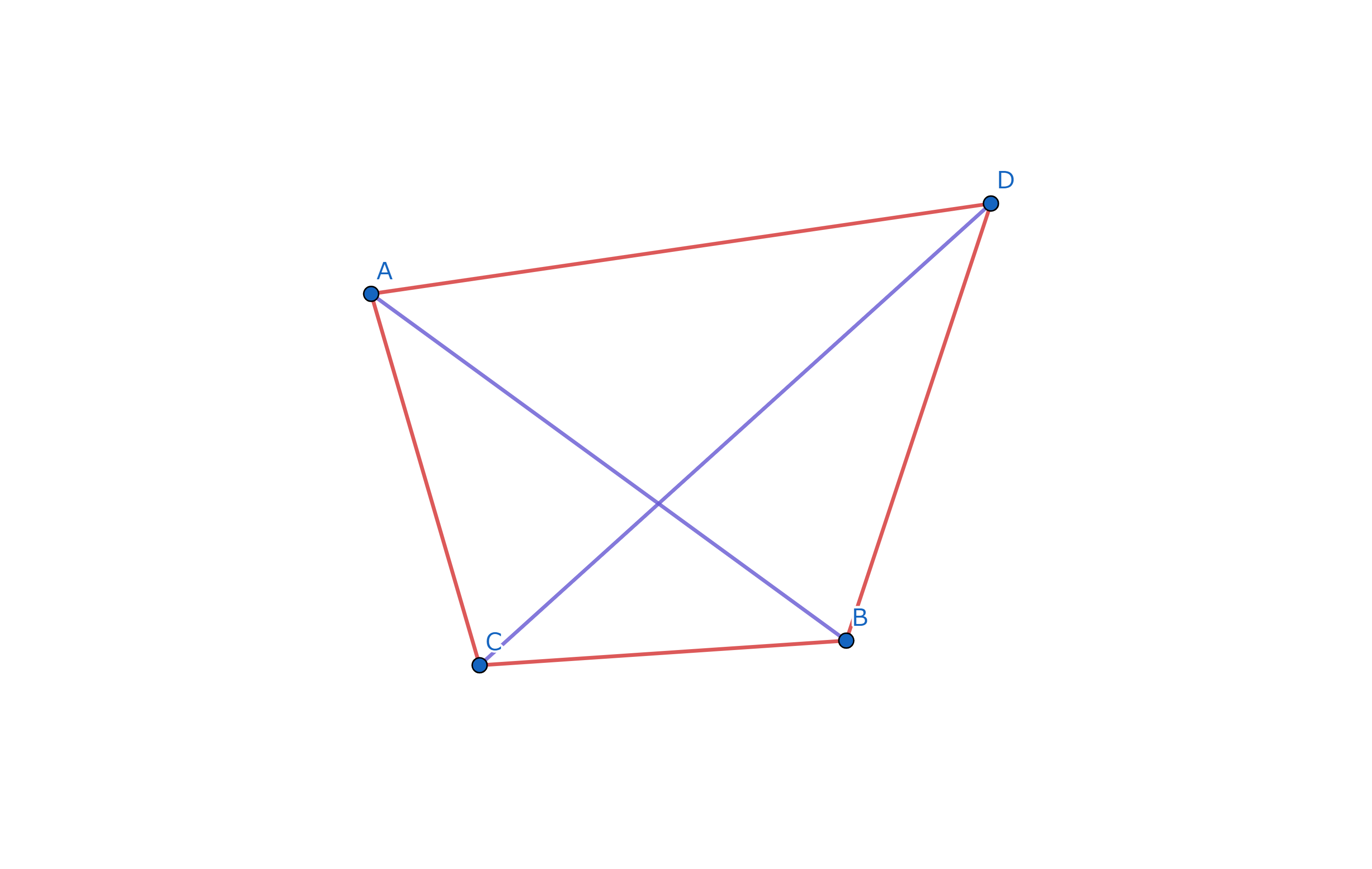
ここで上の様に交わる2つの線分の組（青）の周りには交わらない2つの線分の組（赤）が２つ存在することが分かります．このように組にしていくと、トレミーの不等式により交わらない2つの線分の組の大きさの合計は交わる2つの線分の組の大きさより大きいことがわかるので,良い組のほうが悪い組以上であることが恒等的に証明できました．等号成立は１２３４５６が同一円周上にあるときなので方べきの定理からd(A,1)×d(A,2)＝d(A,6)×d(A,5)よってd(A,1)＝d(A,6)より,d(1,2)＝d(5,6)また同様のことを繰り返して,2つめの条件と合わせると6角形123456は正6角形であることがわかるので,等号成立条件はf(0,1)＝f(1,2)＝f(2,3)です．

16　　　数列の大小関係で重みをつけたときの平均

問題

１以上2023以下の整数から相異なる59個の整数を選び大きい順に並べて得た数列$$a_1,a_2,a_3,\ldots,a_{59}$$としてありうるすべてについて,以下の値Sを求め、その平均を求めてください．
$$S＝\sum_{k=1}^{59}(60-k)a_k$$

一言

帰納的に計算することもできますが,ここでは比較的きれいな想定解を示します．

解説

まず以下を展開します．
$$\sum_{1≦i< j≦59}{}|a_i-a_j|$$
$$＝58a_1+56a_2・・・-56a_{58}-58a_{59}$$
これより,
$$2S＝\sum_{1≦i< j≦59}{}|a_i-a_j|+60\sum_{k=1}^{59}a_k$$
より,これを計算すればよく,これらは主客転倒より簡単に計算できて
求める答えは
$$\frac{_{2021}C_{57}\sum_{k=1}^{2022}k(2023-k)+60_{2022}C_{58}\sum_{k=1}^{2023}k}{2_{2023}C_{59}}＝\frac{7105252}{3}$$

おわりに

懸賞問題の自作問題の解説を書きました．ほかの問題についても随時解説を公開します．
書きながら、主客転倒・FPSなどいろんな手法を使う問題が幅広く出題できていてとても良いな~と思いました．不備があればいつでも知らせてください！では．